6.2. Основные принципы помехоустойчивого кодирования

Задача кодирования информации представляется как некоторое преобразование числовых данных в заданной системе счисления. В частном случае эта операция может быть сведена к группированию символов (представление в виде триад и тетрад) или представлению в виде символов позиционной системы счисления. Так как любая позиционная система счисления не несет в себе избыточности информации, и все кодовые комбинации являются разрешенными, использовать такие системы для контроля не представляется возможным.

Помехоустойчивые коды – одно из наиболее эффективных средств обеспечения высокой верности передачи дискретной информации. Создана специальная теория помехоустойчивого кодирования, быстро развивающаяся в последнее время.

Бурное развитие теории помехоустойчивого кодирования связано с внедрением автоматизированных систем, у которых обработка принимаемой информации осуществляется без участия человека. Использование для обработки информации электронных цифровых ычислительных машин предъявляет очень высокие требования к верности передачи информации.

Теорема Шеннона для дискретного канала с помехами утверждает, что вероятность ошибок за счет действия в канале помех может быть обеспечена сколь угодно малой путем выбора соответствующего способа кодирования сигналов. Из этой теоремы вытекает весьма важный вывод о том, что наличие помех не накладывает принципиально ограничений на верность передачи.

Теорема не указывает конкретного способа кодирования, но из нее следует, что при выборе каждого символа кодовой комбинации необходимо стараться, чтобы он нес максимальную информацию. Следовательно, каж­дый символ должен принимать значения 0 и 1 по возможности с равными вероятностями и каждый выбор должен быть независим от значений предыдущих символов.

При отсутствии статистической взаимосвязи между буквами конструк­тивные методы построения эффективных кодов были даны впервые К. Шенноном и Н. Фано. Их методики существенно не различаются, поэто­му соответствующий код получил название кода Шеннона-Фано.

Код строится следующим образом: буквы алфавита сообщений выпи­сываются в таблицу в порядке убывания вероятностей. Затем они разделя­ются на две группы так, чтобы суммы вероятностей в каждой из групп бы­ли по возможности одинаковы. Всем буквам верхней половины в качестве первого символа приписывается 1, а всем нижним — 0. Каждая из получен­ных групп, в свою очередь, разбивается на две подгруппы с одинаковыми суммарными вероятностями и т. д. Процесс повторяется до тех пор, пока в каждой подгруппе останется по одной букве.

Рассмотрим алфавит из восьми букв (Таблица 4 .6). Ясно, что при обычном (не учитывающем статистических характеристик) кодировании для представления каждой буквы требуется три символа.

Таблица 4.6 - Алфавит из восьми букв

Буквы	Вероятности	Кодовые комбинации
Z1	0,22	11
Z2	0,20	101
Z3	0,16	100
Z4	0,16	01
Z5	0,10	001
Z6	0,10	0001
Z7	0,04	00001
Z8	0,02	00000

Вычислим энтропию набора букв:

и среднее число символов на букву

где п(z_i) — число символов в кодовой комбинации, соответствующей букве z_i. Значения z и lср не очень различаются по величине.

Рассмотренная методика Шеннона-Фано не всегда приводит к однозначному построению кода. Ведь при разбиении на подгруппы можно сделать большей по вероятности как верхнюю, так и нижнюю подгруппу.

Множество вероятностей в предыдущей таблице можно было разбить иначе (Таблица 4 .7).

Таблица 4.7 - Множество вероятностей

Буквы	Вероятности	Кодовые комбинации
Z1	0,22	11
Z2	0,20	10
Z3	0,16	011
Z4	0,16	010
Z5	0,10	001
Z6	0,10	0001
Z7	0,04	00001
Z8	0,02	00000

При этом среднее число символов на букву оказывается равным 2,80. Таким образом, построенный код может оказаться не самым лучшим. При построении эффективных кодов с основанием q>2 неопределенность становится еще больше.

От указанного недостатка свободна методика Д. Хаффмена. Она гарантирует однозначное построение кода с наименьшим для данного распределения вероятностей средним числом символов на букву.

Таблица 4.8 – Код Д. Хаффмена

Для двоичного кода методика сводится к следующему. Буквы алфавита сообщений выписываются в основной столбец в порядке убывания вероятностей. Две последние буквы объединяются в одну вспомогательную букву, которой приписывается суммарная вероятность. Вероятности букв, не участвовавших в объединении, и полученная суммарная вероятность снова располагаются в порядке убывания вероятностей в дополнительном столбце, а две последние объединяются. Процесс продолжается до тех пор, пока не получим единственную вспомогательную букву с вероятностью, равной единице.

Для составления кодовой комбинации, соответствующей данному сообщению, необходимо проследить путь перехода сообщений по строкам и столбцам таблицы. Для наглядности строится кодовое дерево. Из точки, соответствующей вероятности 1, направляются две ветви, причем ветви с большей вероятностью присваивается символ 1, а с меньшей — 0. Такое последовательное ветвление продолжаем до тех пор, пока не дойдем до каждой буквы (Рисунок 6 .35).

Рисунок 6.35 - Кодовое дерево

Теперь, двигаясь по кодовому дереву сверху вниз, можно записать для каждой буквы соответствующую ей кодовую комбинацию:

Z1	Z2	Z4	Z5	Z6	Z7	Z8
01	00	110	100	1011	10101	10100

В теореме Шеннона не говорится о том, как нужно строить помехоустойчивые коды. На этот вопрос отвечает теория помехоустойчивого кодирования.

Рассмотрим сущность помехоустойчивого кодирования, а также некоторые теоремы и определения, относящиеся к теории такого кодирования.

Под помехоустойчивыми или корректирующими кодами понимают коды, позволяющие обнаружить и устранить ошибки, происходящие при передаче из-за влияния помех.

Для выяснения идеи помехоустойчивого кодирования рассмотрим двоичный код, нашедший на практике наиболее широкое применение.

Количество разрядов n в кодовой комбинации принято называть длиной или значностью кода. Каждый разряд может принимать значение 0 или 1. Количество единиц в кодовой комбинации называют весом кодовой комбинации и обозначают .

Например, кодовая комбинация 100101100 характеризуется значностью n=9 и весом =4.

Степень отличия любых двух кодовых комбинаций данного кода характеризуется так называемым расстоянием между кодами d. Оно выражается числом позиций или символов, в которых комбинации отличаются одна от другой. Кодовое расстояние есть минимальное расстояние между кодовым комбинациями данного кода, оно определяется как вес суммы по модулю два кодовых комбинаций. Например, для определения расстояния между комбинациями 100101100 и 110110101 необходимо просуммировать их по модулю два

1

+

00101100

110110101

010011001

Полученная в результате суммирования новая кодовая комбинация характеризуется весом =4. Следовательно, расстояние между исходными кодовыми комбинациями d=4.

Ошибки, вследствие воздействия помех, появляются в том, что в одном или нескольких разрядах кодовой комбинации нули переходят в единицы и, наоборот, единицы переходят в нули. В результате создается новая ложная кодовая комбинация.

Если ошибки происходят только в одном разряде кодовой комбинации, то такие ошибки называются однократными. При наличии ошибок в двух, трех и т.д. разрядах ошибки называются двукратными, трехкратными и т.д.

Для указания мест в кодовой комбинации, где имеются искажения символов, используется вектор ошибки . Вектор ошибки n-разрядного кода – это n-разрядная комбинация, единицы в которой указывают положение искаженных символов кодовой комбинации. Например, если для пятиразрядного кода вектор ошибки имеет =01100, то это значит, что имеют место ошибки в третьем и четвертом разрядах кодовой комбинации.

Вес вектора ошибки характеризует кратность ошибки. Сумма по модулю для искажений кодовой комбинации и вектора ошибки дает исходную неискаженную комбинацию.

Помехоустойчивость кодирования обеспечивается за счет введения избыточности в кодовые комбинации. Это значит, что из n символов кодовой комбинации для передачи информации используется k<n символов. Следовательно, из общего числа возможных кодовых комбинаций для передачи информации используется только комбинаций. В соответствии с этим все множества возможных кодовых комбинаций делятся на две группы. В первую группу входит множество разрешенных комбинаций. Вторая группа включает в себя множество запрещенных комбинаций.

Если на приемной стороне установлено, что принятая комбинация относится к группе разрешенных, то считается, что сигнал пришел без искажений. В противном случае делается вывод, что принятая комбинация искажена. Однако это справедливо лишь для таких помех, когда исключена возможность перехода одних разрешенных комбинаций в другие.

В общем случае каждая из N разрешенных комбинаций может трансформироваться в любую из N₀ возможных комбинаций, т.е. всего имеется N*N₀ возможных случаев передачи (Рисунок 6 .36), из них N случаев безошибочной передачи (на Рисунок 6 .36 обозначены жирными линиями), N(N-1) случаев перехода в другие разрешенные комбинации (на Рисунок 6 .36обозначены пунктирными линиями) и N(N₀- N) случаев перехода в запрещенные комбинации (на Рисунок 6 .36 обозначены штрих пунктирными линиями).

Таким образом, не все искажения могут быть обнаружены. Доля обнаруживаемых ошибочных комбинаций составляет

Для использования данного кода в качестве исправляющего, множество запрещенных кодовых комбинаций разбивается на N непересекающихся подмножеств M_k . Каждое из множеств M_k ставится в соответствие одной из разрешенных комбинаций.

Если принятая запрещенная комбинация принадлежит подмножеству M_i , то считается, что передана комбинация A_i (Рисунок 6 .36).

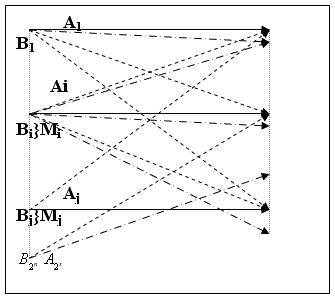
Рисунок 6.36 – Схема передачи комбинаций

Ошибка будет исправлена в тех случаях, когда полученная комбинация действительно образовалась из комбинации A_i. Таким образом, ошибка исправляется в случаях, равных количеству запрещенных комбинаций. Доля исправляемых ошибочных комбинаций от общего числа обнаруживаемых ошибочных комбинаций составляет

Способ разбиения на подмножества зависит от того, какие ошибки должны исправляться данным кодом.