4.2.5Периодические сигналы

Функция x(t) называется периодической, если при некотором постоянном Т выполняется равенство:

x(t)=x(t+nT),

где Т – период функции, n – любое целое (положительное или отрицательное) число, а аргумент t принимает значение из области определения этой функции.

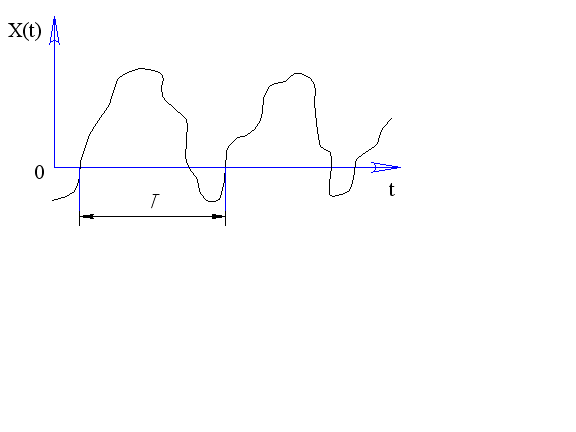
Рисунок 4.10 – График периодической функции

Периодическая функция x(t) с периодом Т обладает следующим свойством: интеграл от этой функции, взятый на интервале длиной Т, не изменяется при изменении пределов интегрирования при условии, что длина интервала интегрирования остается равной Т.

В общем случае сигнал представляет собой сложное колебание, поэтому возникает необходимость представить сложную функцию x(t), определяющую сигнал через простые функции.

Для представления сигналов в частотной области широко используют два частных случая разложения функции в ортогональные ряды: тригонометрическая форма разложения и комплексная.

Рассмотрим их.

4.2.5.1Тригонометрическая форма

Любой периодический сигнал x(t), удовлетворяющий условию Дирихле (x(t) – ограниченая, кусочно-непрерывная, имеет на протяжении периода конечное число экстремумов), может быть представлен в виде ряда Фурье по тригонометрическим функциям:

.

Это выражение указывает на то, что периодическая функция x(t), имеющая период Т может быть разложена по sin и cos углов, кратных углу .

Если период функции x(t) равен Т, то основная круговая частота будет , тогда в формуле разложения x(t) значения коэффициентов a₀, a_k, b_k определяется формулами:

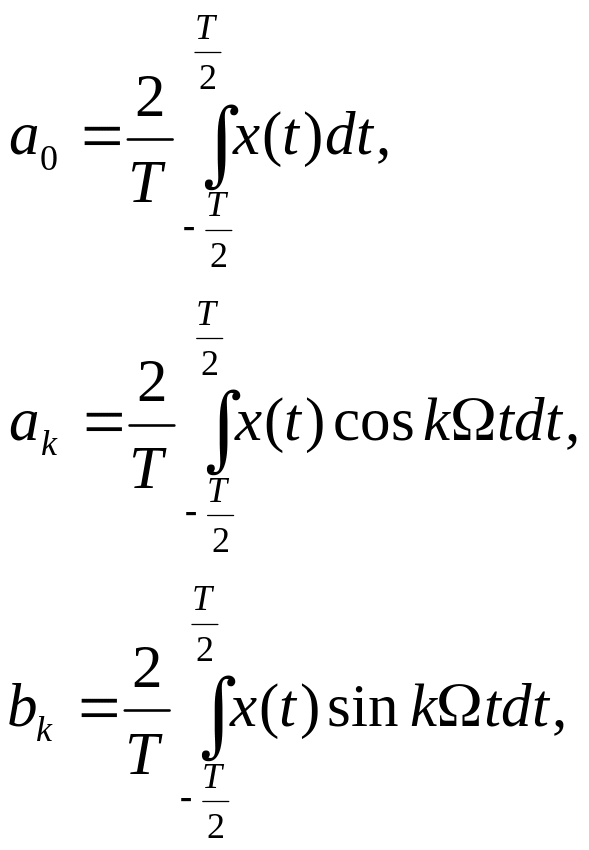
k= 1, 2, 3

Зная коэффициенты a_k и b_k , можно определить значения амплитуды и начальной фазы  k-й гармоники.

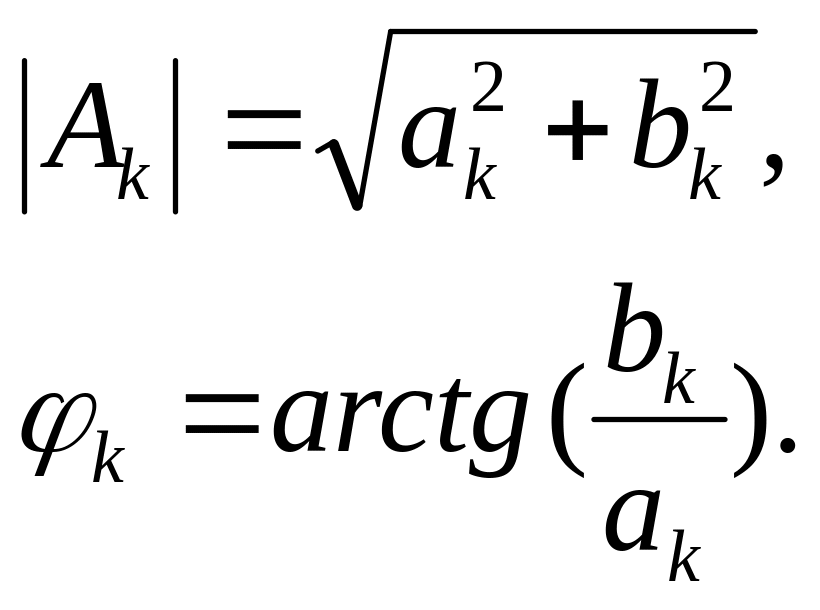
4.2.5.2Комплексная форма

В математическом отношении удобнее оперировать комплексной формой ряда Фурье. Её получают, применяя преобразование Эйлера

Комплексная форма имеет вид:

(2.1)

(2.2)

является комплексной амплитудой k-й гармоники для k=0, 2, 3,…

Формулы: ( 2 .1) именуются парой преобразования Фурье. Формула ( 2 .1) даёт временное описание сигнала x(t), если известны комплексные амплитуды C_k её гармонических составляющих. Совокупность операций, в результате выполнения которых могут быть определены гармоники периодической функции x(t), называется гармоническим анализом.

4.2.5.3Определение погрешности

При разложении периодических функций на сумму гармоник на практике часто ограничиваются несколькими первыми гармониками, а остальные не учитываются. Приближенно представляя функцию x(t) с помощью тригонометрического многочлена вида

можно получить большую или меньшую ошибку представления в зависимости от способа выбора коэффициентов многочлена . Оценить величину ошибки наиболее удобно с помощью средней квадратичной погрешности , определяемой для периодической функции x(t) с периодом T=2 равенством:

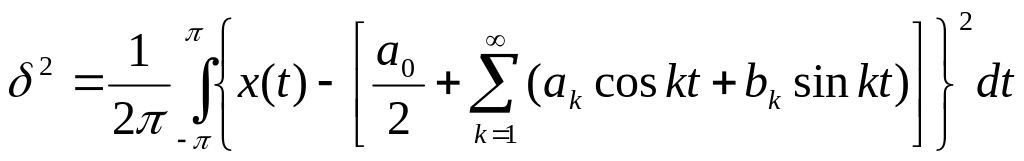
4.2.5.4Спектр

Совокупности коэффициентов a_k, b_k, k=1, 2, 3,…, разложения периодической функции x(t) в ряд Фурье называется частотными спектрами этой функции Совокупность амплитуд и соответствующих частот гармоник принято называть спектром амплитуд.

Совокупность амплитуд и соответствующих частот гармоник называется спектром фаз.

Спектр амплитуд и спектр фаз однозначно определяют сигнал. Однако для многих практических задач достаточно ограничиться спектром амплитуд.

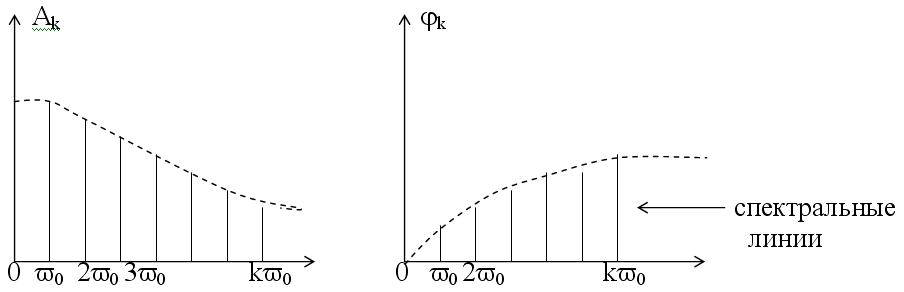
Рисунок 4.11 - Спектр амплитуд и спектр фаз

Характерной особенностью спектра периодического сигнала является его прерывистость (дискретность). Расстояние между соседними спектральными линиями одинаковое и равно частоте основной гармоники.