5.3.2. Матричное представление линейных (систематических) кодов. Коды Хемминга.

В матричной форме систематическое кодирование задается порождающей матрицей G_k×n, тогда:

B_1×n= A_1×k G_k×n,

где B_{1× n}= [ ] - вектор-строка кодового слова;

A_{1× k} = [ ] - вектор-строка информационного слова;

G_k×n- порождающая матрица размером (kxn).

Порождающую матрицу G_k×n можно представить в виде:

G_k×n= [I_k×k P_k×r],

где I_k×k - единичная матрица по числу информационных символов;

P_k×r - правило формирования проверочных символов.

Заметим, что в матрице P_k×r включаются именно коэффициенты , которые и дают правило формирования проверочных символов.

Для рассмотренного ранее примера порождающая матрица будет иметь вид:

1 G4×7 =	0	0	0	0	1	1
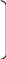
0	1	0	0	1	0	1
0	0	1	0	1	1	0
0	0	0	1	1	1	1

Тогда можно определить любой вектор кодовой комбинации В по заданному вектору А, например:

Для A=[1010], найдем кодовое слово:

Напомним правила арифметики по модулю 2:

Сложение			Умножение
	0	1			0	1
0	0	1		0	0	0
1	1	0		1	0	1

B=[1010] =[1010101]

Проверим по правилу формирования проверочных символов:

,

,

.

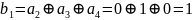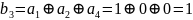Для любого систематического кода с порождающей матрицей G_k×n в интересах его декодирования определяет проверочную матрицу

H_r×n= [P^T _k×r I_r×r],

где I_r×r – единичная матрица;

P^T_k×r - транспонированная матрица правила формирования проверочных символов.

Каждый столбец матрицы H_r×n соответствует синдрому некоторого символа кодовой комбинации:

Первые k-столбцов – синдромам информационных символов, а последние r-столбцов – синдромам проверочных символов.

Единицы в каждой строке проверочной матрицы H_r×n показывают, какие из a_j, информационные символы нужно сложить по модулю 2, чтобы получить соответствующие проверочные b_i, , т.е. правило их формирования.

Процесс декодирования сводится к выполнению следующей операции:

,

где - вектор-строка размерностью 1 r, называемый синдромом кода;

- вектор-строка размерностью 1 n, характеризующий принятую кодовую комбинацию;

- транспонированная проверочная матрица.

Или

Если в принятой кодовой комбинации отсутствуют ошибки, то

Где 0=[0,0,…,0] – нулевой вектор-строка размерностью 1 r.

В противном случае C≠0.

Таким образом, декодирование систематических кодов основано на матричном умножении по модулю 2, которое осуществляется обычным образом, но с учетом правил умножения и сложения по модулю 2.

Проверочная матрица для рассмотренного ранее кода (7,4) будет иметь вид:

P_{k×r = ;} [P^T _k×r I_r×r]=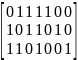

Проведем декодирование принятой кодовой комбинации

=[1010101] при условии одиночной ошибки в четвертом разряде 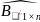=[1011101]

Найдем матрицу синдромов для принятой комбинации с ошибкой :

=[1011 101] =[111]

Сопоставляя полученный синдром со столбцами проверочной матрицы или строками транспонированной матрицы, находим его соответствие синдрому четвертого информационного символа и приходим к выводу, что ошибка произошла в символе a₄. Следовательно, в принятой ошибочной комбинации надо исправить символ a₄ на противоположный, тогда получим кодовую комбинацию с исправленной ошибкой в четвертом разряде

=[101  101]

Если кодовая комбинация записана (сформирована) так, что синдром будет указывать на номер разряда (равен ему) в принятой комбинации, в котором произошла ошибка, то такой линейный (систематический) код называют кодом Хэмминга.

В нашем примере, если символы алфавита a и b расположить [a₄a₃a₂a₁b₃b₂b₁], то синдром [111] 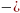указывал бы на седьмой разряд (отсчет разрядов ведется справа налево) кодового слова, т.е. на то, чтобы ошибка произошла в символе a_4.

Пример: Самостоятельно проверить, что надо изменить в рассмотренном выше примере, чтобы код (7,4) можно было бы назвать кодом Хэмминга. Изменятся ли при этом порождающая и проверочная матрицы?

Таким образом, порождающая G_k×n и проверочная H_r×n матрицы обычно используются для построения кодеков. Поскольку между этими матрицами существует однозначное соответствие

G_k×n= [I_k×k P_k×r] и H_r×n= [P^T _k×r I_r×r], то в принципе организовать кодирование и декодирование можно с помощью одной из них.

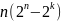Тогда, при использовании линейных (систематических) кодов, нет необходимости хранить в памяти декодера все разрешенные кодовые комбинации N_p= , а это - двоичных символов), и подмножества запрещенных кодовых комбинаций(N-Np) (а это - двоичных символов), для организации декодирования по методу максимального правдоподобия. Достаточно для кодирования и синдромного декодирования запомнить проверочную H_r×n матрицу, которая занимает объем памяти (r×n) ячеек.