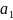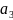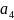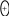- •Кафедра Информационные системы
- •Тамбов 2010
- •5.1. Классификация помехоустойчивых кодов.
- •5.2 Параметры (характеристики) помехоустойчивых кодов и их границы. Корректирующие свойства кодов.
- •5.3.Линейные (систематические) коды.
- •5.3.1.Механизмы кодирования и синдромного декодирования.
- •5.3.2. Матричное представление линейных (систематических) кодов. Коды Хемминга.
5.3.Линейные (систематические) коды.
5.3.1.Механизмы кодирования и синдромного декодирования.
В
линейных (систематических) кодах
информационные символы при кодировании
не изменяются, а проверочные символы
получаются в результате суммирования
по модулю 2 определенного числа
информационных символов. Запишем
разрешенную кодовую комбинацию
систематического кода (n,k)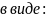
 ,
,
где
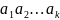 –
множество информационных символов;
–
множество информационных символов;
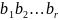 –
множество
проверочных символов.
–
множество
проверочных символов.
Тогда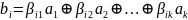 ,
,
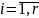 ,
,
где
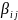 ,
j=
,
j= – весовые коэффициенты принимающие
значения 0 или 1 в зависимости от того,
участвует или нет данный информационный
символ
– весовые коэффициенты принимающие
значения 0 или 1 в зависимости от того,
участвует или нет данный информационный
символ
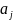 в формировании проверочного символа
в формировании проверочного символа
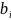 .
.
Обнаружение и исправление ошибок систематическим кодом сводится к определению и последующему анализу синдрома или вектора ошибок.
В медицине термин синдром используют для обозначения сочетания признаков, характеризующих определенное болезненное состояние организма.
Под
синдромом понимают совокупность
символов
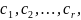 сформированную, путем сложения по
модулю 2 принятых проверочных символов
сформированную, путем сложения по
модулю 2 принятых проверочных символов
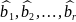 и вычисленных проверочных символов
и вычисленных проверочных символов


Вычисленные
символы
получаются из принятых информационных
символов
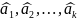 по тому же правилу, которое используется
для формирования проверочных символов.
по тому же правилу, которое используется
для формирования проверочных символов.
Если при приеме информационных и проверочных символов не произошло ошибок, то принятые и вычисленные проверочные символы будут равны. В этом случае все разряды синдрома будут равны нулю. Таким образом, нулевой синдром соответствует случаю отсутствия ошибок.
Если же в принятой комбинации есть ошибки, то в разрядах синдрома появятся единицы. Это и есть способ обнаружения ошибок систематическим кодом, который лежит в основе синдромного декодирования.
Если
код имеет минимальное кодовое расстояние
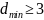 ,
то он способен исправлять ошибки. Это
означает, что по виду синдрома можно
определить номер ошибочной позиции
принятой кодовой комбинации.
,
то он способен исправлять ошибки. Это
означает, что по виду синдрома можно
определить номер ошибочной позиции
принятой кодовой комбинации.
Процедура построения систематического кода, способного обнаруживать ошибки, сводится к выбору весовых коэффициентов таким образом, чтобы синдром, рассматриваемый как двоичное число, указывал номер ошибочной позиции.
Пример: Пусть требуется построить систематический код длиной n=7, способный исправлять одиночные ошибки. Тогда из =2t+1 находим, что может быть, =3. Пользуясь условием для границы Хемминга, находим минимальное число проверочных символов:
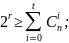
При
t=1,
n=7;
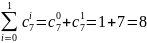
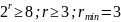
Тогда число информационных символов k=n-r=4.
Следовательно, необходимо построить код (7,4), кодовые комбинации которого имеют вид:
 ,
атрии проверочных символа находятся
путем суммирования информационных
символов по правилу:
,
атрии проверочных символа находятся
путем суммирования информационных
символов по правилу:
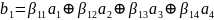 ,
,
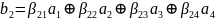 ,
,
 .
.
Найдем эти весовые коэффициенты . Для этого запишем все возможные трехразрядные кодовые комбинации синдрома:
000, 001, 010, 100, 011, 101, 110, 111
И присвоим их ошибочным символам кодовой комбинации.
Когда
в принятой комбинации
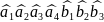 нет ошибок, синдром будет состоять из
трех путей:
нет ошибок, синдром будет состоять из
трех путей:

Появление одной единицы в синдроме связано с ошибками в проверочной части кодовой комбинации.
100
→ ошибка в
 ,
,
010→
ошибка в
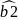 ,
,
001→
ошибка в
 .
.
А появление большего числа единиц в синдроме связано с ошибками в информационной части.
Присвоим информационным символам с ошибками оставшиеся синдромы в порядке возрастания их двоичных чисел (по существу безразлично, какие двоичные числа можно присваивать информационным символам):
011→
ошибка в
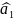 ,
,
101→
ошибка в
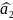 ,
,
110→
ошибка в
 ,
,
111→
ошибка в
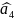 .
.
Итак, каждому символу кодовой комбинации соответствует двоичное число, представляющее синдром:
Синдром |
Символ кодовой комбинации с ошибкой |
|
000 |
нет ошибок |
|
001 |
b3 |
|
010 |
b2 |
|
011 |
a1 |
|
100 |
b1 |
|
101 |
a2 |
|
110 |
a3 |
|
111 |
a4 |
|
Осталось
определить весовые коэффициенты
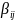 .
Для этого необходимо подобрать их так,
чтобы при возникновении ошибки в
.
Для этого необходимо подобрать их так,
чтобы при возникновении ошибки в
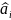 - символе появлялся бы соответствующий
этой ошибке синдром.
- символе появлялся бы соответствующий
этой ошибке синдром.
Например, для появления синдрома 011, соответствующего ошибке в

Весовые
коэффициенты при символе a1
должны иметь значения
 =0,
=0,
 =
1,
=
1,
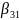 =1.
=1.
Аналогично, появление остальных синдромов обеспечивают коэффициенты:
101
(ошибка в
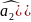 →
→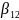 =1,
=1,
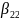 =0,
=0,
 =1,
=1,
110
(ошибка в
)
→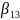 =1,
=1,
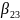 =1,
=1,
 =0,
=0,
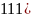 )→
)→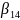 =1,
=1,
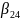 =1,
=1,
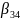 =1.
=1.
Окончательное правило формирования проверочных символов принимает вид:
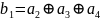 ,
,
 ,
,
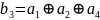 .
.
Формирование систематического кода (7,4) по такому правилу поясняется следующим рисунком:
|
|
|
|
|
|
|
|
|
|
|