4.3.1. Метод кодирования Шеннона - Фано.
Буквы исходного алфавита записываются в порядке убывающей вероятности. Упорядоченное таким образом множество букв разбивается так, чтобы суммарные вероятности двух подмножеств были примерно равными. Всем буквам верхней половины в качестве первого символа кода присваивают 1, а буквам нижней половины – 0. Затем каждое подмножество снова разбивается на два подмножества с соблюдением того же условия примерного равенства вероятностей и с тем же условием присвоения кодовых элементов в качестве второго символа. Такое разбиение продолжается до тех пор, пока в подмножестве не останется только по одной букве кодового алфавита.
Пример: Провести эффективное кодирование ансамбля из восьми букв (знаков).
Буква xi |
Вероятности pi |
Кодовая последовательность |
Длина кодового слова ni |
pini |
-pilog2pi |
|||
Номер разбиения |
||||||||
1 |
2 |
3 |
4 |
|||||
x1 |
0,25 |
1 |
1 |
|
|
2 |
0,5 |
0,50 |
x2 |
0,25 |
1 |
0 |
|
|
2 |
0,5 |
0,50 |
x3 |
0,15 |
0 |
1 |
1 |
|
3 |
0,45 |
0,41 |
x4 |
0,15 |
0 |
1 |
0 |
|
3 |
45 |
0,41 |
x5 |
0,05 |
0 |
0 |
1 |
1 |
4 |
0,2 |
0,22 |
x6 |
0,05 |
0 |
0 |
1 |
0 |
4 |
0,2 |
0,22 |
x7 |
0,05 |
0 |
0 |
0 |
1 |
4 |
0,2 |
0,22 |
x8 |
0,05 |
0 |
0 |
0 |
0 |
4 |
0,2 |
0,22 |
=
=
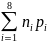(0,25*2+0,25*2+0,15*3+0,15*3+0,05*4+0,05*4+0,05*4+0,15*4)=2,7 бит
=
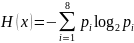- (2*0,25*log2
0,25 + 2*0,15*log2
0,15 + 4*0,05*log20,05)
= 2,7 бит
=
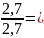1
Метод Шеннона - Фано не всегда приводит к однозначному построению кода, так как при разбиении на подмножества можно сделать большей по вероятности как верхнюю, так и нижнюю подгруппу. Следовательно, такое кодирование хотя и является эффективным, но не всегда будет оптимальным.
4.3.2. Метод кодирования Хаффмана.
Этот метод кодирования всегда дает оптимальный код, т.е. получаемая является минимальной.
Буквы алфавита сообщения выписываются в порядке убывания вероятностей. Две последние буквы объединяют в один составной знак, которому приписывают суммарную вероятность. Заново переупорядочивают буквы по убыванию вероятностей и снова объединяют пару с наименьшими вероятностями. Продолжают этот процесс до тех пор, пока все значения не будут объединены. Такая процедура называется редукцией.
Затем строится кодовое дерево из точки, соответствующей вероятности 1, причем ребрам с большей вероятностью присваивают 1, а с меньшей - 0. Двигаясь по кодовому дереву от корня к оконечным узлам, можно записать кодовое слово для каждой буквы исходного алфавита.
Пример 1 (ПЗ№8):
Знаки(буквы) |
Вероятность |
Редукция |
Кодовое слово по кодовому дереву |
||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
||||
x1 |
0,22 |
0,22 |
0,22 |
0,26 |
0,32 |
0,42 |
0,58 |
1 |
01 |
||
x2 |
0,20 |
0,20 |
0,20 |
0,22 |
0,26 |
0,32 |
0,42 |
|
00 |
||
x3 |
0,16 |
0,16 |
0,16 |
0,20 |
0,22 |
0,26 |
|
|
111 |
||
x4 |
0,16 |
0,16 |
0,16 |
0,16 |
0,20 |
|
|
|
110 |
||
x5 |
0,1 |
0,1 |
0,16 |
0,16 |
|
|
|
|
100 |
||
x6 |
0,1 |
0,1 |
0,1 |
|
|
|
|
|
1011 |
||
x7 |
0,04 |
0,06 |
|
|
|
|
|
|
10101 |
||
x8 |
0,02 |
|
|
|
|
|
|
|
10100 |
||
корень
Пример №2 :
Буква xi |
a
|
b |
c |
d |
e |
f |
Вероятности pi |
0,05 |
0,15 |
0,05 |
0,4 |
0,2 |
0,15 |
Кодовое слово |
1001 |
110 |
1000 |
0 |
111 |
101 |
Длина кодового слова ni |
4 |
3 |
4 |
1 |
3 |
3 |
I
I
способ: Редукция по уровням.
xi |
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
x8 |
pi |
0,22 |
0,20 |
0,16 |
0,16 |
0,1 |
0,1 |
0,04 |
0,02 |
код |
01 |
00 |
111 |
110 |
100 |
1011 |
10100 |
10110 |
ni |
2 |
2 |
3 |
3 |
3 |
4 |
5 |
5 |
nipi |
0,44 |
0,4 |
0,48 |
0,48 |
0,3 |
0,4 |
0,2 |
0,1 |
-pilog2pi |
|
|
|
|
|
|
|
|
= =2,8
=
=
Заметим:
1) Во втором способе при построении кодового дерева для присвоения ребрам его значений 1 и 0 необходимо использовать тот же принцип: 1 – ребру с большей вероятностью, 0 – ребру с меньшей вероятностью
2) В случае, когда в процедуре редукции несколько знаков имеют одинаковые вероятности, необходимо выбрать для очередного объединения те два из них, которые до этого имели наименьшее число объединений. Этим достигается выравнивание длин кодовых слов.
Из примера видно, что чем больше разница между вероятностями букв исходного алфавита, тем больше выигрыш кода Хаффмана по сравнению с простым блоковым кодированием.
Декодирование кода Хаффмана легко представить, используя кодовое дерево. Принятая кодовая комбинация анализируется посимвольно, в результате чего, начиная с корня дерева, мы попадаем в оконечный узел, соответствующий принятой букве исходного алфавита.
При всей простоте коды Хаффмана обладают недостатками:
1.Различные длины кодовых слов приводят к неравномерным задержкам кодирования.
2.Сжатие снижает избыточность, что соответственно повышает предрасположенность к распространению ошибок, т.е. один ошибочно принятый бит может привести к тому, что все последующие символы будут декодироваться неверно.
3.Предполагаются априорные знания вероятности букв, которые на практике не известны, а их оценки часто бывают затруднены.