12. Волновые явления (интерференция, дифракция, поляризация).

Распространение в однородных средах(поляризация)

При распространении волн изменения их амплитуды и скорости в пространстве и появление дополнительных гармоник зависят от свойств анизотропности среды, сквозь которую проходят волны, границ, а также характера излучения источников волн.

Чаще волны в некоторой среде затухают, что связано с диссипативными процессами внутри среды. Но в случае некоторых специальным образом подготовленных метастабильных сред амплитуда волны может, наоборот, усиливаться (пример: генерация лазерного излучения). Наличие в среде резонансных подструктур обусловливает и появление кратковременного и длительного послесвечения.

На практике монохроматические волны встречаются очень редко. Максимально приближаются к монохроматическому излучение лазера, мазера, радиоантенны. Условием монохроматичности является удалённость области рассмотрения от переднего фронта волны, а также характер излучения источника. Если источник некогерентный, излучение состоит из наложения большого числа отрезков волн. Для описания когерентности сигнала вводится понятие время когерентности и длина когерентности ^[8].

Учитывая свойства субстанции, в которой распространяется излучение, а также сложный в общем случае спектр сигнала, вводится понятие фазовой и групповой скорости волны, то есть скорость «центра тяжести» волнового пакета.

Групповая и фазовая скорости совпадают только для линейных волн в средах без дисперсии. Для нелинейных волн групповая скорость может быть как больше, так и меньше фазовой скорости. Однако иногда принято считать, что когда речь идёт о скоростях, близких к скорости света, проявляется заведомое неравноправие между групповой и фазовой скоростями. Фазовая скорость не является ни скоростью движения материального объекта, ни скоростью передачи данных, поэтому она может превышать скорость света, не приводя при этом ни к каким нарушениям теории относительности. Вместе с тем, это немного не точно. Базовые постулаты теории относительности, как и теоретические построения на них, основываются на распространении света в пустоте, т.е. в среде без дисперсии, в которой фазовая и групповая скорости одинаковы. В вакууме фазовая и групповая скорость распространения света одинаковы, в воздухе, воде и некоторых других средах разница между ними пренебрежимо мала и ею в большинстве случаев можно пренебрегать^[9]. Поэтому если фазовая скорость в среде без дисперсии оказывается большей или меньшей скорости света, то такое же значение будет принимать и групповая скорость.

Групповая скорость характеризует скорость движения сгустка энергии, переносимой волновым пакетом, и потому в большинстве случаев не превышает скорость света. Также при распространении волны в метастабильной среде удаётся в определённых случаях добиться групповой скорости, превышающей скорость света в среде, как например при распространении света в сероуглероде.

Поскольку волна переносит энергию и импульс, то её можно использовать для передачи информации. При этом возникает вопрос о максимально возможной скорости передачи информации с помощью волн данного типа (чаще всего речь идёт об электромагнитных волнах). При этом скорость передачи информации никогда не может превышать скорости света в вакууме, что было подтверждено экспериментально даже для волн, в которых групповая скорость превышает скорость света в среде распространения.

Интерференция волн — взаимное увеличение или уменьшение результирующей амплитуды двух или нескольких когерентных волн, одновременно распространяющихся в пространстве.^[1] Сопровождается чередованием максимумов и минимумов (пучностей) интенсивности в пространстве. Результат интерференции (интерференционная картина) зависит от разности фаз накладывающихся волн.

Интерферировать могут все волны, однако устойчивая интерференционная картина будет наблюдаться только в том случае, если волны имеют одинаковую частоту и колебания в них не ортогональны. Интерференция может быть стационарной и нестационарной. Стационарную интерференционную картину могут давать только полностью когерентные волны. Например, две сферические волны на поверхности воды, распространяющиеся от двух когерентных точечных источников, при интерференции дадут результирующую волну, фронтом которой будет сфера.

При интерференции энергия волн перераспределяется в пространстве.^[1] Это не противоречит закону сохранения энергии потому, что в среднем, для большой области пространства, энергия результирующей волны равна сумме энергий интерферирующих волн. ^[2]

При наложении некогерентных волн средняя величина квадрата амплитуды (т.е. интенсивность результирующей волны) равна сумме квадратов амплитуд (интенсивностей) накладывающихся волн. Энергия результирующих колебаний каждой точки среды равна сумме энергий ее колебаний, обусловленных всеми некогерентными волнами в отдельности. Именно отличие результирующей интенсивности волнового процесса от суммы интенсивностей его составляющих и есть признак интерференции.^[3]

Если в некоторой однородной и изотропной среде два точечных источника возбуждают сферические волны, то в произвольной точке пространства M может происходить наложение волн в соответствии с принципом суперпозиции (наложения): каждая точка среды, куда приходят две или несколько волн, принимает участие в колебаниях, вызванных каждой волной в отдельности. Таким образом волны не взаимодействуют друг с другом и распространяются независимо друг от друга.

Две одновременно распространяющиеся синусоидальные сферические волны и , созданные точечными источниками B₁ и B₂, вызовут в точке M колебание, которое, по принципу суперпозиции, описывается формулой . Согласно формуле сферической волны:

,

,

где

и – фазы распространяющихся волн

и — волновые числа ( )

и — циклические частоты каждой волны

и — начальные фазы,

и — расстояния от точки М до точечных источников B₁ и B₂

В результирующей волне , амплитуда и фаза определяются формулами:

,

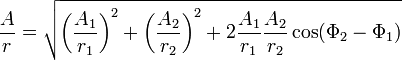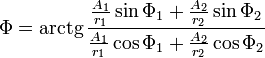
Когерентность волн

Волны и возбуждающие их источники называются когерентными, если разность фаз волн не зависит от времени. Волны и возбуждающие их источники называются некогерентными, если разность фаз волн изменяется с течением времени. Формула для разности :

, где , ,

– скорость распространения волны, одинаковая для обеих волн в данной среде. В приведенном выше выражении от времени зависит только первый член. Две синусоидальные волны когерентны, если их частоты одинаковы ( ), и некогерентны, если их частоты различны.

Для когерентных волн ( ) при условии

,

.

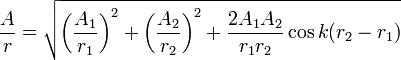Амплитуда результирующих колебаний в любой точке среды не зависит от времени. Косинус равен единице, а амплитуда колебаний в результирующей волне максимальна во всех точках среды, для которых , где (m-целое) или , (так как )

Величина называется геометрической разностью хода волн от их источников B₁ и B₂, до рассматриваемой точки среды.

Амплитуда колебаний в результирующей волне минимальна во всех точках среды, для которых

, где (m-натуральное),

или

.

При наложении когерентных волн квадрат амплитуды и энергия результирующей волны отличны от суммы квадратов амплитуд и суммы энергий накладываемых волн.

Поляриза́ция волн — явление нарушения симметрии распределения возмущений в поперечной волне (например, напряжённостей электрического или магнитного полей в электромагнитных волнах) относительно направления её распространения. В продольной волне поляризация возникнуть не может, так как возмущения в этом типе волн всегда совпадают с направлением распространения.^[1]

Поперечная волна характеризуется двумя направлениями: волновым вектором и вектором амплитуды, всегда перпендикулярным к волновому вектору. Так что в трёхмерном пространстве имеется ещё одна степень свободы — вращение вокруг волнового вектора.

Причиной возникновения поляризации волн может быть:

1 несимметричная генерация волн в источнике возмущения;

2 анизотропность среды распространения волн;

3 преломление и отражение на границе двух сред.

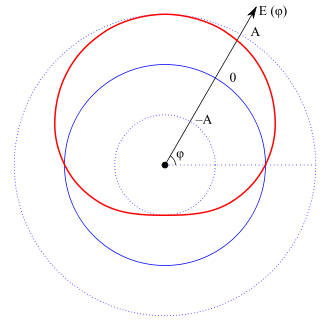
Зависимость мгновенных потенциалов при круговой поляризации

Основными являются два вида поляризации:

1 линейная — колебания возмущения происходят в какой-то одной плоскости. В таком случае говорят о «плоско-поляризованной волне»;

2 круговая — конец вектора амплитуды описывает окружность в плоскости колебаний. В зависимости от направления вращения вектора может быть правой или левой.

На основе этих двух или только круговой можно сформировать и другие, более сложные виды поляризации. Например, эллиптическая. В общем случае, круговая поляризация — вещь теоретическая, на практике же говорят об эллиптической поляризации — с левым или правым направлением вращения.

Поляризация описывается Фигурами Лиссажу и соответствует сложению поперечных колебаний равной частоты.

Дифра́кция во́лн (лат. diffractus — буквально разломанный, переломанный, огибание препятствия волнами) — явление, которое проявляет себя как отклонение от законов геометрической оптики при распространении волн. Она представляет собой универсальное волновое явление и характеризуется одними и теми же законами при наблюдении волновых полей разной природы.

Дифракция неразрывно связана с явлением интерференции. Более того, само явление дифракции зачастую трактуют как случай интерференции ограниченных в пространстве волн (интерференция вторичных волн). Общим свойством всех эффектов дифракции является зависимость степени её проявления от соотношения между длиной волны и характерным размером неоднородностей среды , либо неоднородностей структуры самой волны. Наиболее заметно они проявляются при размерах неоднородностей, сравнимых с длиной волны. При размерах неоднородностей, существенно превышающих длину волны (на 3—4 порядка и более), явлением дифракции, как правило, можно пренебречь. В последнем случае распространение волн с высокой степенью точности описывается законами геометрической оптики. С другой стороны, если размер неоднородностей среды много меньше длины волны, то в таком случае дифракции проявляет себя в виде эффекта рассеяния волн.^[1]

Изначально явление дифракции трактовалось как огибание волной препятствия, то есть проникновение волны в область геометрической тени. С точки зрения современной науки определение дифракции как огибания светом препятствия признается недостаточным (слишком узким) и не вполне адекватным. Так, с дифракцией связывают весьма широкий круг явлений, возникающих при распространении волн (в случае учёта их пространственного ограничения) в неоднородных средах.

Дифракция волн может проявляться:

1 в преобразовании пространственной структуры волн. В одних случаях такое преобразование можно рассматривать как «огибание» волнами препятствий, в других случаях — как расширение угла распространения волновых пучков или их отклонение в определённом направлении;

2 в разложении волн по их частотному спектру;

3 в преобразовании поляризации волн;

4 в изменении фазовой структуры волн.

Наиболее хорошо изучена дифракция электромагнитных (в частности, оптических) и акустических волн, а также гравитационно-капиллярных волн (волны на поверхности жидкости).