6. Затухающие колебания.

Затухающие колебания — колебания, энергия которых уменьшается с течением времени. Бесконечно длящийся процесс вида в природе невозможен. Свободные колебания любого осциллятора рано или поздно затухают и прекращаются. Поэтому на практике обычно имеют дело с затухающими колебаниями. Они характеризуются тем, что амплитуда колебаний A является убывающей функцией. Обычно затухание происходит под действием сил сопротивления среды, наиболее часто выражаемых линейной зависимостью от скорости колебаний или её квадрата.

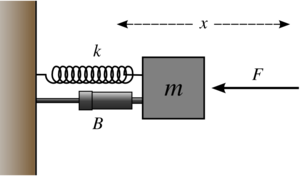
Затухающие колебания пружинного маятника

Модель пружинного маятника. B — механизм, обеспечивающий затухание. F — внешняя сила (в примере не присутствует).

Пускай имеется система, состоящая из пружины (подчиняющейся закону Гука), один конец которой жёстко закреплён, а на другом находится тело массой m. Колебания совершаются в среде, где сила сопротивления пропорциональна скорости с коэффициентом c (см. вязкое трение).

Тогда второй закон Ньютона для рассматриваемой системы запишется так:

где  — сила сопротивления,  — сила упругости

, , то есть

или в дифференциальной форме

где k — коэффициент упругости в законе Гука, c — коэффициент сопротивления, устанавливающий соотношение между скоростью движения грузика и возникающей при этом силой сопротивления.Для упрощения вводятся следующие обозначения:

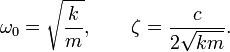
Величину называют собственной частотой системы,  — коэффициентом затухания.

Тогда дифференциальное уравнение принимает вид

Сделав замену , получают характеристическое уравнение

Корни которого вычисляются по следующей формуле

Решения

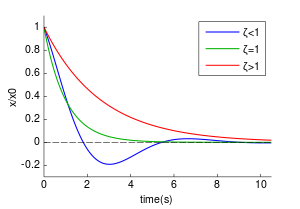
Зависимость графиков колебаний от значения .

В зависимости от величины коэффициента затухания решение разделяется на три возможных варианта.

Апериодичность

Если , то имеется два действительных корня, и решение дифференциального уравнения принимает вид:

В этом случае колебания с самого начала экспоненциально затухают.

Граница апериодичности

Если , два действительных корня совпадают , и решением уравнения является:

В данном случае может иметь место вре́менный рост, но потом — экспоненциальное затухание.

Слабое затухание

Если , то решением характеристического уравнения являются два комплексно сопряжённых корня

Тогда решением исходного дифференциального уравнения является

Где  — собственная частота затухающих колебаний.

Константы и в каждом из случаев определяются из начальных условий:

7. Вынужденные колебания. Резонанс.

Вынужденные колебания — колебания, происходящие под воздействием внешних сил, меняющихся во времени.

Автоколебания отличаются от вынужденных колебаний тем, что последние вызваны периодическим внешним воздействием и происходят с частотой этого воздействия, в то время как возникновение автоколебаний и их частота определяются внутренними свойствами самой автоколебательной системы.

Наиболее простой и содержательный пример вынужденных колебаний можно получить из рассмотрения гармонического осциллятора и вынуждающей силы, которая изменяется по закону: .

Вынужденные колебания гармонического осциллятора

Консервативный гармонический осциллятор

Второй закон Ньютона для такого осциллятора запишется в виде: . Если ввести обозначения: и заменить ускорение на вторую производную от координаты по времени, то получим следующее обыкновенное дифференциальное уравнение:

Решением этого уравнения будет сумма общего решения однородного уравнения и частного решения неоднородного. Общее решение однородного уравнения было уже получено здесь и оно имеет вид:

,

где  — произвольные постоянные, которые определяются из начальных условий.

Найдём частное решение. Для этого подставим в уравнение решение вида: и получим значение для константы:

Тогда окончательное решение запишется в виде:

Резона́нс (фр. resonance, от лат. resono — откликаюсь) — явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при приближении частоты внешнего воздействия к некоторым значениям (резонансным частотам), определяемым свойствами системы. Увеличение амплитуды — это лишь следствие резонанса, а причина — совпадение внешней (возбуждающей) частоты с внутренней (собственной) частотой колебательной системы. При помощи явления резонанса можно выделить и/или усилить даже весьма слабые периодические колебания. Резонанс — явление, заключающееся в том, что при некоторой частоте вынуждающей силы колебательная система оказывается особенно отзывчивой на действие этой силы. Степень отзывчивости в теории колебаний описывается величиной, называемой добротность. Явление резонанса впервые было описано Галилео Галилеем в 1602 г в работах, посвященных исследованию маятников и музыкальных струн.

Из решения видно, что при частоте вынуждающей силы, равной частоте свободных колебаний, оно не пригодно — возникает резонанс, то есть «неограниченный» линейный рост амплитуды со временем. Из курса математического анализа известно, что решение в этом случае надо искать в виде: .

Подставим этот анзац в дифференциальное уравнение и получим, что :

Таким образом, колебания в резонансе будут описываться следующим соотношением:

Затухающий гармонический осциллятор

Второй закон Ньютона:

.

Переобозначения:

Дифференциальное уравнение:

Его решение будет строиться, как сумма решений однородного уравнения и частного решения неоднородного. Анализ однородного уравнения приведён здесь. Получим и проанализируем частное решение.

Запишем вынуждающую силу следующим образом: , тогда решение будем искать в виде: .

Подставим это решение в уравнение и найдём выражение для A:

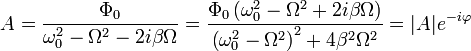
где

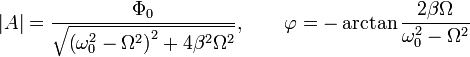
Полное решение имеет вид:

,

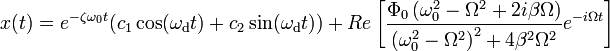где  — собственная частота затухающих колебаний.

Константы и в каждом из случаев определяются из начальных условий:

В этом случае, в отличие от осциллятора без трения, амплитуда колебаний в резонансе имеет конечную величину.

Если мы рассмотрим устоявший процесс, то есть ситуацию при , то решение однородного уравнения будет стремиться к нулю и останется только частное решение:

Это означает, что при система «забывает» начальные условия, и характер колебаний зависит только от вынуждающей силы.

Работа, совершаемая вынуждающей силой за время , равна , а мощность . Из уравнения

следует, что

Если учесть, что при установившихся вынужденных колебаниях

то тогда средняя за период мощность:

Работа за период