1 . Колебания. Гармонические колебания. Уравнение гармонических колебаний.

Колебания - движения, обладающие той или иной степенью повторяемости.

Колебания почти всегда связаны с попеременным превращением энергии одной формы проявления в другую форму.

Колебания различной физической природы имеют много общих закономерностей и тесно взаимосвязаны c волнами. Поэтому исследованиями этих закономерностей занимается обобщённая теория колебаний и волн. Принципиальное отличие от волн: при колебаниях не происходит переноса энергии, это, так сказать, «местные» преобразования энергии.

По физической природе:

Механические (звук, вибрация)

Электромагнитные (свет, радиоволны, тепловые)

Смешанного типа — комбинации вышеперечисленных

По характеру взаимодействия с окружающей средой:

Вынужденные — колебания, протекающие в системе под влиянием внешнего периодического воздействия. Примеры: листья на деревьях, поднятие и опускание руки. При вынужденных колебаниях может возникнуть явление резонанса: резкое возрастание амплитуды колебаний при совпадении собственной частоты осциллятора и частоты внешнего воздействия.

Свободные (или собственные) — это колебания в системе под действием внутренних сил, после того как система выведена из состояния равновесия (в реальных условиях свободные колебания всегда затухающие). Простейшими примерами свободных колебаний являются колебания груза, прикреплённого к пружине, или груза, подвешенного на нити.

Автоколебания — колебания, при которых система имеет запас потенциальной энергии, расходующейся на совершение колебаний (пример такой системы — механические часы). Характерным отличием автоколебаний от свободных колебаний является, то что их амплитуда определяется свойствами самой системы, а не начальными условиями.

Параметрические — колебания, возникающие при изменении какого-либо параметра колебательной системы в результате внешнего воздействия.

Случайные — колебания, при которых внешняя или параметрическая нагрузка является случайным процессом.

Характеристики

Амплитуда — максимальное отклонение колеблющейся величины от некоторого усреднённого её значения для системы, (м)

Период — промежуток времени, через который повторяются какие-либо показатели состояния системы (система совершает одно полное колебание), (с)

Частота — число колебаний в единицу времени, (Гц, с⁻¹).

Период колебаний и частота  — обратные величины;

и

В круговых или циклических процессах вместо характеристики «частота» используется понятие круговая (циклическая) частота (рад/с, Гц, с⁻¹), показывающая число колебаний за единиц времени:

Смещение — отклонение тела от положения равновесия. Обозначение Х, Единица измерения метр.

Фаза колебаний — определяет смещение в любой момент времени, то есть определяет состояние колебательной системы.

Гармоническое колебание — колебания, при которых физическая (или любая другая) величина изменяется с течением времени по синусоидальному или косинусоидальному закону. Кинематическое уравнение гармонических колебаний имеет вид

или

,

где х — смещение (отклонение) колеблющейся точки от положения равновесия в момент времени t; А — амплитуда колебаний, это величина, определяющая максимальное отклонение колеблющейся точки от положения равновесия; ω — циклическая частота, величина, показывающая число полных колебаний происходящих в течение 2π секунд  — полная фаза колебаний,  — начальная фаза колебаний.

Обобщенное гармоническое колебание в дифференциальном виде

(Любое нетривиальное^[1] решение этого дифференциального уравнения — есть гармоническое колебание с циклической частотой )

2. Колебания под действием упругих сил, пружинный маятник.

Пружинный маятник состоит из пружины и массивного шара, насаженного на горизонтальный стержень, вдоль которого он может скользить. Пусть на пружине укреплен шарик с отверстием, который скользит вдоль направляющей оси (стержня). На рис. 7.2,а показано положение шара в состоянии покоя; на рис. 7.2,б - максимальное сжатие и на рис. 7.2,в -произвольное положение шарика.

Под действием возвращающей силы, равной силе сжатия, шарик будет совершать колебания. Сила сжатия F = -kx , где k - коэффициент жесткости пружины. Знак минус показывает, что направление силы F и смещение х противоположны. Потенциальная энергия сжатой пружины

кинетическая .

Для вывода уравнения движения шарика необходимо связать х и t. Вывод основывается на законе сохранения энергии. Полная механическая энергия равна сумме кинетической и потенциальной энергии системы. В данном случае :

. В положении б) : .

Так как в рассматриваемом движении выполняется закон сохранения механической энергии, можно записать:

. Определим отсюда скорость:

Но в свою очередь и, следовательно, . Разделим переменные . Интегрируя это выражение, получим: ,

где - постоянная интегрирования. Из последнего следует, что

(7.2)

Сравнивая (7.1) с (7.2), получаем

(7.3)

Таким образом, под действием упругой силы тело совершает гармонические колебания. Силы иной природы, чем упругие, но в которых выполняется условие F = -kx, называются квазиупругими. Под действием этих сил тела тоже совершают гармонические колебания. При этом:

смещение:
скорость:
ускорение:

3. Математический маятник.

Математи́ческий ма́ятник — осциллятор, представляющий собой механическую систему, состоящую из материальной точки, находящейся на невесомой нерастяжимой нити или на невесомом стержне в однородном поле сил тяготения^[1]. Период малых собственных колебаний математического маятника длины L неподвижно подвешенного в однородном поле тяжести с ускорением свободного падения g равен

и не зависит от амплитуды колебаний и массы маятника.

Плоский математический маятник со стержнем — система с одной степенью свободы. Если же стержень заменить на растяжимую нить, то это система с двумя степенями свободы со связью. Пример школьной задачи, в которой важен переход от одной к двум степеням свободы.

При малых колебаниях физический маятник колеблется так же, как математический с приведённой длиной.

Уравнение колебаний маятника

Колебания математического маятника описываются обыкновенным дифференциальным уравнением вида

где ― положительная константа, определяемая исключительно из параметров маятника. Неизвестная функция ― это угол отклонения маятника в момент от нижнего положения равновесия, выраженный в радианах; , где ― длина подвеса, ― ускорение свободного падения. Уравнение малых колебаний маятника около нижнего положения равновесия (т. н. гармоническое уравнение) имеет вид:

.

Решения уравнения движения

Гармонические колебания

Маятник, совершающий малые колебания, движется по синусоиде. Поскольку уравнение движения является обыкновенным ДУ второго порядка, для определения закона движения маятника необходимо задать два начальных условия — координату и скорость, из которых определяются две независимых константы:

где  — амплитуда колебаний маятника,  — начальная фаза колебаний,  — циклическая частота, которая определяется из уравнения движения. Движение, совершаемое маятником, называется гармоническими колебаниями

Нелинейный маятник

Для маятника, совершающего колебания с большой амплитудой, закон движения более сложен:

где  — это синус Якоби. Для он является периодической функцией, при малых совпадает с обычным тригонометрическим синусом.

Параметр определяется выражением

где  — энергия маятника в единицах t⁻².

Период колебаний нелинейного маятника

где K — эллиптический интеграл первого рода.

Для вычислений практически удобно разлагать эллиптический интеграл в ряд:

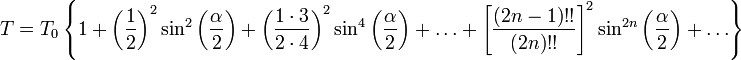, где  — период малых колебаний,  — максимальный угол отклонения маятника от вертикали.

При углах до 1 радиана (≈60°) с приемлемой точностью (ошибка менее 1 %) можно ограничиться первым приближением:

.

Точная формула периода, с квадратичной сходимостью для любого угла максимального отклонения, обсуждается на страницах 1096-1097 Сентябрьского выпуска заметок американского математического общества 2012 г.^[3]:

где -- арифметико-геометрическое среднее числел 1 и .