18.Непрерывные случайные величины.

• Говорят, что случайная величина Х имеет плотность вероятности или плотность распределения вероятностей , если существует функция p(x) такая, что функция распределения (1).

• Случайная величина называется непрерывной, если она имеет плотность распределения.

Свойства плотности распределения.

1. .

2. Плотность распределения—неотрицательная функция: .

Поскольку F(x)—неубывающая функция, то F’(x)≥0. Следовательно —неотриц. функция.

Геометрически это свойство означает, что график плотности распределения расположен либо над осью ох, либо на этой оси. График плотности распределения называют кривой распределения.

3. Несобственный интеграл от плотности распределения в пределах от -∞ до +∞ равен единице:

.

В формуле (1) подставим х=+∞,

Поскольку , то .

4. В ероятность того, что непрерывная случайная величина Х примет значение из множества В, равна интегралу по множеству В от плотности распределения .

19.Равномерное, показательное и нормальное распределение и их характеристики.

• Г оворят, что случайная величина Х равномерно распределена на отрезке [a, b], если она непрерывна и имеет плотность вероятности:

Ф ункция распределения равномерно распределенной случайной величины X.

Примером равномерно распределенной случ-й вел-ны может служить Х-координата точки, науд. брошенной на [a, b].

• Говорят, что случайная величина Х имеет показательное распределение с параметром λ>0, если она непрерывна и имеет плотность распределения

; обозначают Х~M(λ).

Ф ункция распределения показательно распределенной случайной величины Х.

• Говорят, что случайная величинf Х имеет нормальное распределение с параметрами a, G², если она непрерывна и имеет плотность . Обозначение Х~N(a, G²), те Х имеет нормальное распределение с параметрами a, G².

График плотности нормально распределенной случайной величины имеет вид:

• Математическим ожиданием или средним значением непрерывной случайной величины Х с плотностью p(x) называется число 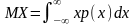при условии, что этот интеграл сходится абсолютно.

• Дисперсией непрерывной случайной величины Х называется число . Если случайная величина имеет плотность p(x), .

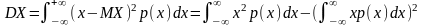Математическое ожидание и дисперсия непрерывных случайных величин обладают теми же свойствами, что и для дискретных случайных величин.