
- •11 Теорема Пуассона
- •12. Теорема (локальная теорема Муавра-Лапласа).
- •13. Случайные величины.
- •14. Дискретные случ.Величины. Закон распределения
- •15. Математическое ожидание
- •16. Дисперсия
- •17. Теоремы о мат. Ожидании и дисперсии. Начальные и центральные моменты
- •18.Непрерывные случайные величины.
- •Свойства плотности распределения.
- •19.Равномерное, показательное и нормальное распределение и их характеристики.
- •20. Теорема о нормальном распред-нии. Критерии независимости величин.
- •21. Случайный вектор. Св-ва функции распред-я случ вектора.
- •Функция распределения случайного вектора неубывающая по каждому аргументу.
- •22. Дискрет и непрерывный случ вектор. Св-ва плотности распределения
- •Теорема 1. Пусть —непрерывный случайный вектор. Тогда случайные величины и —непрерывны, причем
- •23. Числовые характеристики системы двух случайных величин. Ковариация, корреляция. Ассиметрия и эксцесс.
- •25.26.Эмпирическая функция распределения. Полигон и гистограмма.
- •27. Точечные оценки неизвестных параметров.
11 Теорема Пуассона
Т
 еорема.
Если вероятность р появления события
А в каждом испытании при неограниченном
возрастании числа испытаний n
изменяется таким образом, что некоторое
событие А появится ровно k
раз в n
независимых исп-х стремится к величине
, то есть .
еорема.
Если вероятность р появления события
А в каждом испытании при неограниченном
возрастании числа испытаний n
изменяется таким образом, что некоторое
событие А появится ровно k
раз в n
независимых исп-х стремится к величине
, то есть .
Д оказательство:
По формуле
Бернулли вероятность того, что событие
появится ровно k
раз в n
независимых испытаниях
оказательство:
По формуле
Бернулли вероятность того, что событие
появится ровно k
раз в n
независимых испытаниях ,
где q=1-p.
Отсюда
,
где q=1-p.
Отсюда
 По
условию . Получим
По
условию . Получим


Перейдем к пределу
при
 ,
т.е.
,
т.е.


 .
.
—формула Пуассона.
Теоремой удобно
пользоваться, когда р→0,
 .
Существуют специальные таблицы, в
которых приведены значения вероятностей
для различных а и k.
.
Существуют специальные таблицы, в
которых приведены значения вероятностей
для различных а и k.
Формулой Бернулли удобно пользоваться, когда значение n не очень велико. Если же n достаточно велико, то удобн пользоваться приближенными формулами.
12. Теорема (локальная теорема Муавра-Лапласа).
Если вероятность появления события А в каждом отдельном испытании постоянная и отлична от 0 и 1, т.е. 0<p<1, то вероятность того, что событие А появится ровно k раз в n независимых испытаниях.

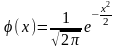
 ,
где ; ,
,
где ; ,
q=1-p.
Без доказательства. Имеются специальные таблицы значений функций φ(х). Нужно учитывать, что функция φ(х)–четная, т.е. φ(х)=φ(-х).
Теорема (интегральная теорема Муавра-Лапласа).
Е сли
вероятность появления события А в
каждом отдельном испытании постоянна
и отлична от 0 и 1, т.е.0<p<1,
то вероятность того, что событие А
появится от k1
до k2
раз в n
независимых испытаниях определяется
выражением:
сли
вероятность появления события А в
каждом отдельном испытании постоянна
и отлична от 0 и 1, т.е.0<p<1,
то вероятность того, что событие А
появится от k1
до k2
раз в n
независимых испытаниях определяется
выражением:
 ,
где
,
где
—функция Лапласа,.


Без доказательства.
Функция
Лапласа—нечетная, т.е.
 .
Значения находят по таблице.
.
Значения находят по таблице.
13. Случайные величины.
Случайной величиной Х называется функция X(w), отображающая пространство элементарных исходов Ω во множестве действительных чисел R.
Функцией распределения случайной величины Х называется функция F(x) действительной переменной х, определяющая вероятность того, что случайная величина Х примет в результате эксперимента значение, меньшее некоторого фиксированного числа х.
 ;
;

Если рассматривать
Х как случайную точку на оси ох, то F(x)
с геометрической точки зрения—это
вероятность того, что случайная точка
Х в результате реализации эксперимента
попадет левее точки х.
![]()
Свойства функции распределения.
Ф
 ункция
распределения F(x)–неубывающая
функция, т.е. для
ункция
распределения F(x)–неубывающая
функция, т.е. для
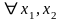 таких что x1<x2
.
таких что x1<x2
.
Для любых


З
 амечание.
Если функция распределения F(x)
непрер-я, то св-во выполняется и при
замене знаков ≤ и < на < и ≤.
амечание.
Если функция распределения F(x)
непрер-я, то св-во выполняется и при
замене знаков ≤ и < на < и ≤.
Функция F(x) непрер. слева.
Вер-сть того, что значение случайной величины Х больше некоторого числа х, вычисляется по формуле.
 .
.

