
- •2. Экспоненциальные функции
- •3. Функции Хаара
- •3. Автокорреляционная функция треугольного импульса
- •1. Телеграфный сигнал
- •2. Белый шум
- •3. Гауссовские процессы
- •1. Последовательная обратная связь по току.
- •2. Параллельная обратная связь по напряжению
- •3. Последовательная обратная связь по напряжению
- •4. Параллельная ос по току.
3. Гауссовские процессы
Статистическая связь между двумя
случайными величинами
![]() определяется
корреляционным моментом:
определяется
корреляционным моментом:
![]() (11)
(11)
Корреляционный момент совпадает с корреляционной функцией, если процесс стационарный. Кроме корреляционного момента, вводят понятие коэффициента корреляции. Коэффициент корреляции:
![]()
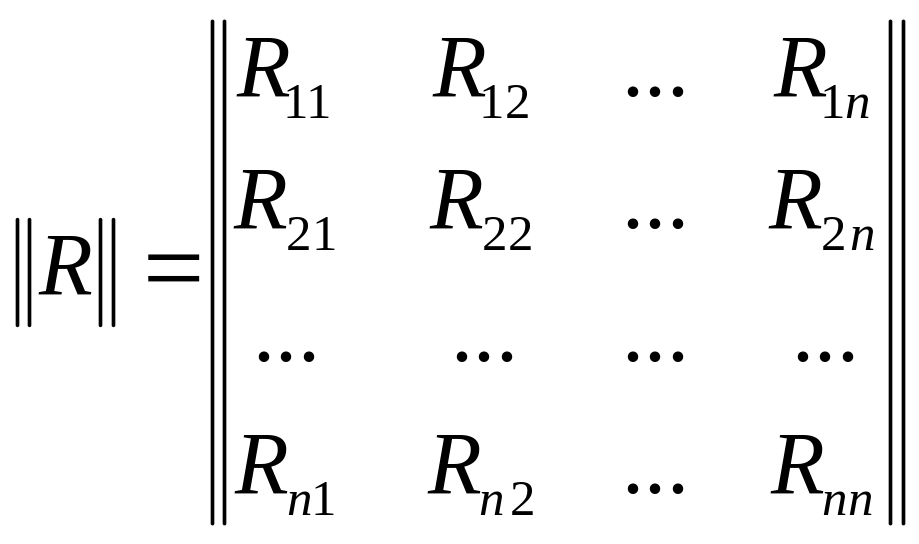
Если процесс определяется -мерным вектором, то
![]()
![]()
![]() записывается
и в форме матрицы
записывается
и в форме матрицы
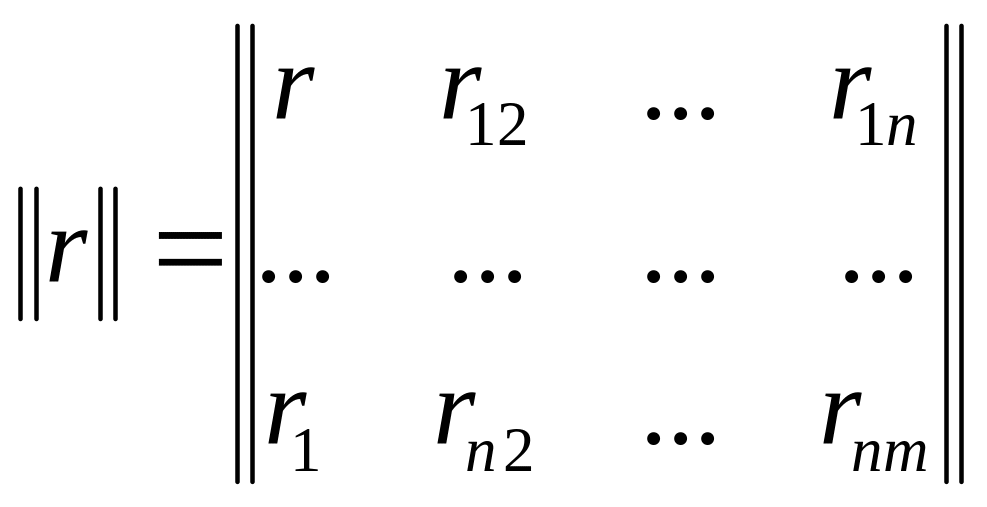
Если процесс стационарный, то
![]()
Процесс называют Гауссовским, если его плотность распределения:
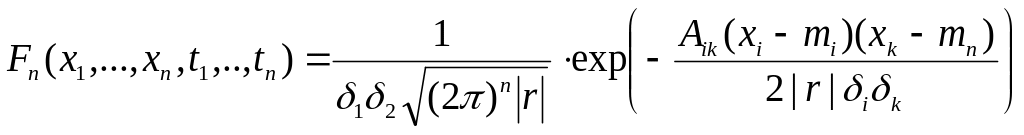
где
![]() -
определитель матрицы,
-
определитель матрицы,
![]() -
алгебраическое дополнение в определителе
-
алгебраическое дополнение в определителе
![]() .
Если процесс стационарный, то зная
корреляционную функцию можно определить
плотность распределения. Так, в частном
случае, функция первого порядка равна:
.
Если процесс стационарный, то зная
корреляционную функцию можно определить
плотность распределения. Так, в частном
случае, функция первого порядка равна:
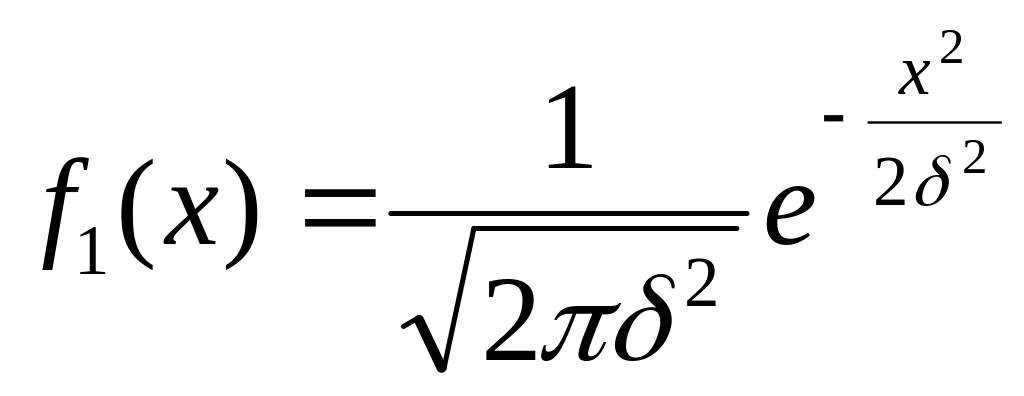
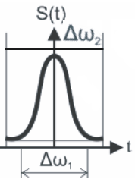
Узкополосые процессы. Аналитические сигналы.
Узкополосные процессы
Наряду с моделями случайных сигналов
рассматривается и постоянные информационные
сигналы. Моделями таких информационных
сигналов служат так называемые
узкополосные сигналы. Такие сигналы
возникают на выходе устройств, работающих
на промежуточных и высоких частотах.
Сигнал называется узкополосным, если
отношение полосы
![]() ,
где
-
полоса чистого сигнала,
,
где
-
полоса чистого сигнала,
![]() ,
,
![]() -
средняя частота
-
средняя частота
![]() .
.
Форма математических моделей узкополосного сигнала
Применим 2 равноценные формы математических моделей.
В 1-й форме сигнал представляется в виде амплитудно-модулированного сигнала:
![]() (13)
(13)
При 2-й форме сигнал представляется в виде суммы двух амплитудно-модулированных колебаний:
![]() (14),
(14),
где
![]() ,
,
![]()
![]()
![]()
Формы представления равноценны и их применение зависит от выбора системы координат (полярной или декартовой).
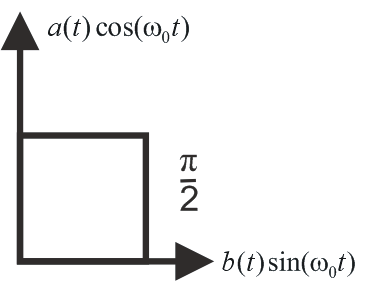
Уравнение (14) можно рассматривать как
ортогональное разложение по одной
гармонике, причем
![]() и
и
![]() представляют
коэффициенты в разложении, кроме того
зависимости
и
дают
возможность сформулировать ряд свойств
для рассмотрения модулированных
сигналов. Функция
называется
синфазной функцией,
- квадратурной.
представляют
коэффициенты в разложении, кроме того
зависимости
и
дают
возможность сформулировать ряд свойств
для рассмотрения модулированных
сигналов. Функция
называется
синфазной функцией,
- квадратурной.
![]()
Функции
![]() представляют
собой малоизменяющиеся функции по
отношению к колебанию с частотой
представляют
собой малоизменяющиеся функции по
отношению к колебанию с частотой
![]() .
.
![]() -
-![]()
Аналитический сигнал
Любой узкополосный сигнал можно представить в двух формах: в виде амплитудно- и частотно-модулированного сигнала:
![]() (1)
(1)
или в виде двух модулированных сигналов.
![]() (2)
(2)
![]()
Две формы равноценны и их применение зависит от выбора системы координат.
Рассмотрим первую форму записи:
![]()
Комплексная амплитуда
![]()
![]()
![]()
Обозначим
![]() (3)
(3)
![]() -
величина сопряженная с сигналом
-
величина сопряженная с сигналом
![]() .
.
Введение комплексной записи сигнала упрощает исследования свойств узкополосных сигналов.
Из определения комплексной величины:
![]() (4)
(4)
Комплексный сигнал
![]() называется аналитическим, если его
реальная и мнимая части удовлетворяют
прямому и обратному преобразованию
Гильберта.
называется аналитическим, если его
реальная и мнимая части удовлетворяют
прямому и обратному преобразованию
Гильберта.
![]() -
прямое преобразование
-
прямое преобразование
![]() (5)
- обратное преобразование
(5)
- обратное преобразование
Рассмотрим более подробно понятие аналитического сигнала.
Применим к сигналу обратное преобразование Фурье:
![]()
![]() -
аналитический сигнал.
-
аналитический сигнал.
Аналитический сигнал определяется
только в области положительных частот,
![]() .
.
![]() ,
замена
,
замена
![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
Определим спектральную плотность
сигнала
![]()
![]()
![]()
Подставляя данные в выражение значения
и![]() с учетом преобразования Гильберта
получаем:
с учетом преобразования Гильберта
получаем:
![]()
![]()
Знаковая функция![]() -
можно рассматривать как результат
прохождения сигнала
через
пассивный четырехполюсник, который
смещает все фазы спектральной плотности
на угол
-
можно рассматривать как результат
прохождения сигнала
через
пассивный четырехполюсник, который
смещает все фазы спектральной плотности
на угол
![]() .
.
В общем виде
![]()
![]()
Из данного выражения следует, что спектр аналитического сигнала существует только в области положительных частот.
Исходя из данных свойств аналитического
сигнала нетрудно получить выражение
для импульсной характеристики
и
корреляционной функции
![]()
![]()
![]()
Взаимная спектральная плотность мощностей:
![]()
![]() -
взаимная корреляционная функция.
-
взаимная корреляционная функция.
Корреляционные функции узкополосного сигнала
По определению корреляционная функция может быть связана со спектральной плотностью преобразованием Хинчина-Винера.
![]()
Рассмотрим наиболее простой случай,
когда![]() и
сигнал будет узкополосным:
и
сигнал будет узкополосным:
![]() ,
,
![]()
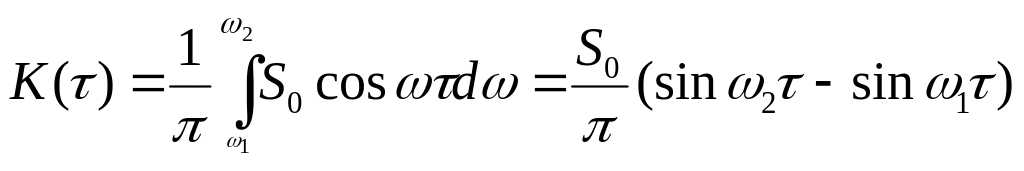
![]()
Сложим 2 уравнения:
![]() (6)
(6)
![]() (7)
(7)
Подставляя значения частот
![]() и
и
![]() в выражение для корреляционной функции,
получим:
в выражение для корреляционной функции,
получим:
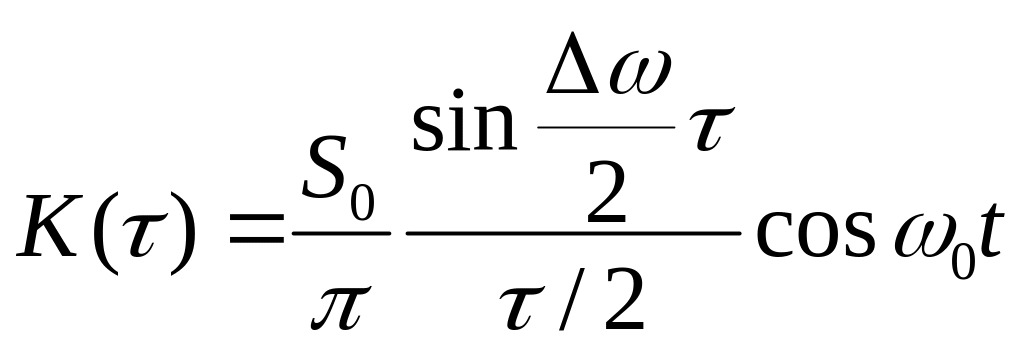
![]()
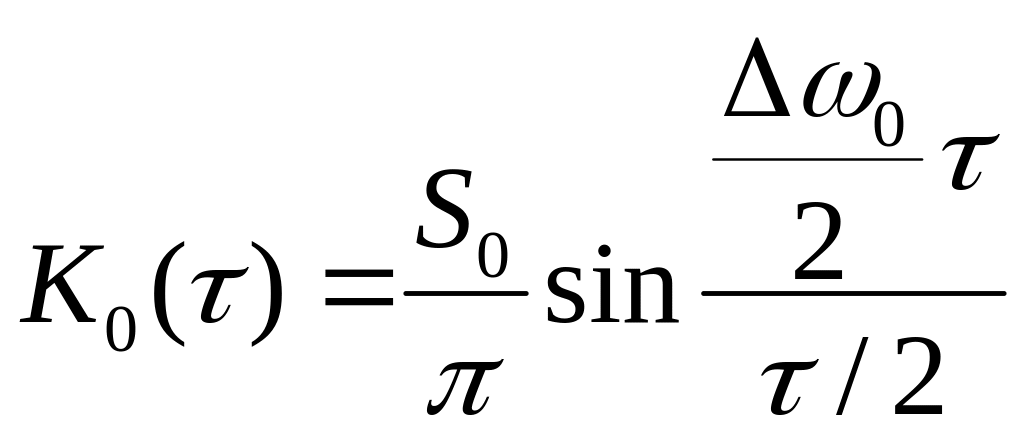 -
корреляционная функция
-
корреляционная функция
Функция огибающей:
![]()
Чтобы найти корреляционную функцию узкополосного сигнала, нужно умножить коэффициент огибающей на косинус гармонического дополнения.
Процессы в колебательном контуре
Последовательный колебательный контур
Рассмотрим процессы, происходящие в последовательном колебательном контуре.
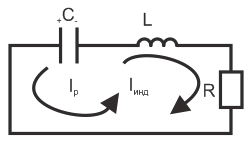
Сообщим заряд конденсатору
![]()
При разряде конденсатора в цепи протекает
ток, т.к. заряд измеряется с течением
времени, следовательно
![]() .
В результате изменения тока во времени
в индуктивности возникает ЭДС самоиндукции.
Минус Связан с правилом Ленца - индукционный
ток всегда имеет такое направление, при
котором он противодействует причинам,
вызывающим появление данного тока
.
В результате изменения тока во времени
в индуктивности возникает ЭДС самоиндукции.
Минус Связан с правилом Ленца - индукционный
ток всегда имеет такое направление, при
котором он противодействует причинам,
вызывающим появление данного тока
![]() (1)
(1)
Для определения зависимости силы тока от времени надо составить уравнение процесса, основанное на втором законе Кирхгофа.
![]() -
второе правило Кирхгофа в контуре. В
контуре будет происходить колебательный
процесс, т.к. электрическая энергия
конденсатора переходит в энергию
магнитного поля.
-
второе правило Кирхгофа в контуре. В
контуре будет происходить колебательный
процесс, т.к. электрическая энергия
конденсатора переходит в энергию
магнитного поля.
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,
![]()
Подставим в уравнение Кирхгофа значение
![]() и
ЭДС
и
ЭДС
![]()
![]()
![]()
Введем обозначение
![]() -
собственная частота.
-
собственная частота.
Решение любого дифференциального
уравнения второго порядка, как правило,
определяется подставкой Эйлера
![]()
Подставим решение в уравнение:
![]() (2)
(2)
![]()
Общее решение определится как
![]() (3),
(3),
![]() -
определяется из начальных условий. Из
(3) следует, что в контуре будут возникать
колебания, только если
-
определяется из начальных условий. Из
(3) следует, что в контуре будут возникать
колебания, только если
![]() ,
если
,
если
![]() ,
то корни будут вещественными и колебания
не происходят.
,
то корни будут вещественными и колебания
не происходят.
![]() (4)
(4)
![]()
![]()
![]() (5)
(5)
Комплексных величин не существует в
природе, чтобы она была вещественной,
надо чтобы
![]() и
и![]() были
комплексно-сопряженными.
были
комплексно-сопряженными.
![]()
![]()
![]()
![]()
Фаза![]() ,
где
,
где
![]() -
начальная фаза
-
начальная фаза
![]()
Коэффициент
![]() (коэффициент
затухания),определяет значение амплитуд.
(коэффициент
затухания),определяет значение амплитуд.
![]() -
декремент амплитуды
-
декремент амплитуды
![]()
![]() (6)
(6)
Вводят параметр добротности![]() (7)
(7)
Выясним физический смысл логического
декремента затухания. Пусть за время
![]() ,
амплитуда колебаний изменяется в
,
амплитуда колебаний изменяется в
![]() раз.
Тогда
раз.
Тогда
![]()
![]()
Логический декремент затухания обратно пропорционален числу колебаний за время, в течение которого амплитуда уменьшается раз. При малых затуханиях
![]()
![]()
![]() -
волновое сопротивление
-
волновое сопротивление
![]()
Добротность
![]() (8)
(8)
Сила тока
![]()
Умножим и разделим на
![]() :
:
![]()
![]()
![]()
Т.к.
![]() -
величина отрицательная, а
-
величина отрицательная, а
![]() -
величина положительная, то, следовательно,
ток будет отставать по фазе на угол
-
величина положительная, то, следовательно,
ток будет отставать по фазе на угол
![]()
![]()
Вынужденные колебания в
![]() -контуре
-контуре
Подключим контур и периодическую ЭДС.
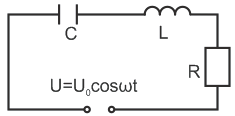
![]()
![]() (9)
(9)
Вынужденные колебания в контуре идут под действием высших гармоник ЭДС.
Решение дифференциального уравнения определяется в виде:
![]()
![]() при
при
![]()
Частное решение найдем методом комплексных
амплитуд. При таком методе гармонические
функции
![]() или
или
![]() заменяется
на
заменяется
на
![]()
![]()
![]() (10)
(10)
![]()
Подставляя (10), получим уравнение для
определения комплексной амплитуды
![]()
![]()
![]()
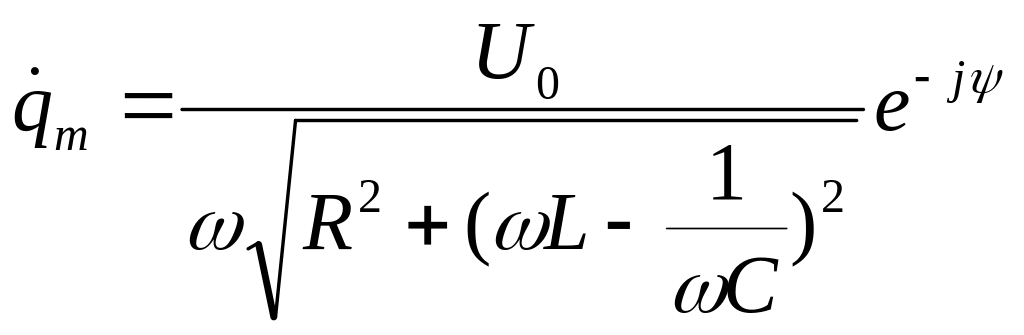 (11)
(11)
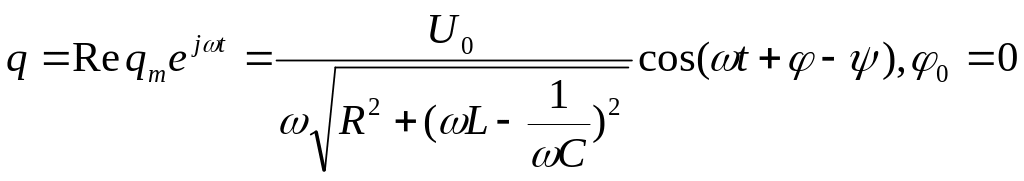
Таким образом, заряд на конденсаторе
отстает по фазе от внешнего напряжения
на угол
![]() ,зависящий
от параметра контура.
,зависящий
от параметра контура.
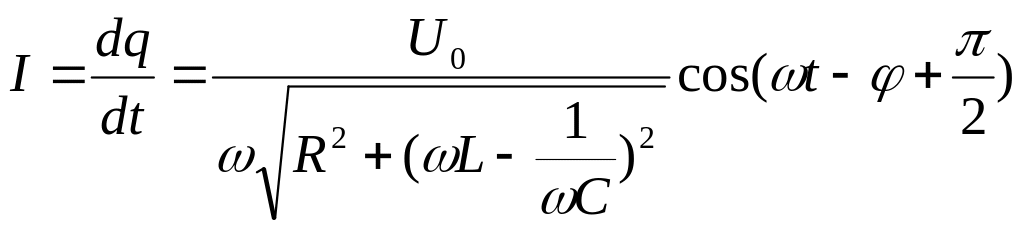 (12)
(12)
Из (12) следует, что сила тока опережает
заряд на конденсаторе на угол
![]() .
.
Определим емкостное и индуктивное сопротивление.
![]()
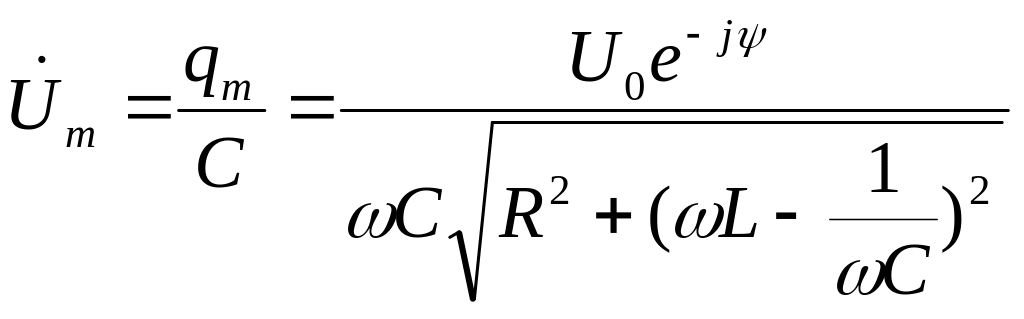
Учитывая выражение для тока, запишем:
![]()
Величина
![]() называется емкостным реактивным
сопротивлением.
называется емкостным реактивным
сопротивлением.
![]()
![]()
Величина
![]() называется индуктивным реактивным
сопротивлением.
называется индуктивным реактивным
сопротивлением.
![]()
![]()
![]()
![]()
Резонанс заряда и силы тока
Амплитуда заряда и силы тока зависят от частоты внешних сигналов, следовательно должна существовать частота, при который амплитуды достигают максимального значения. Такое явление называется резонансом, а частота - резонансной.
![]()
Не вычисляя производные, можно получить
выражение для
![]() .
.
![]()
При резонансе тока резонансная частота равна собственной частоте.
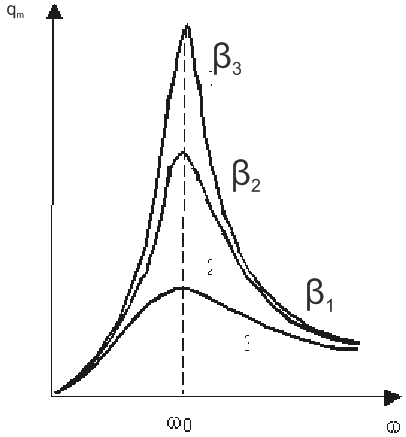
Процессы в контуре примерно изображены резонансными кривыми.
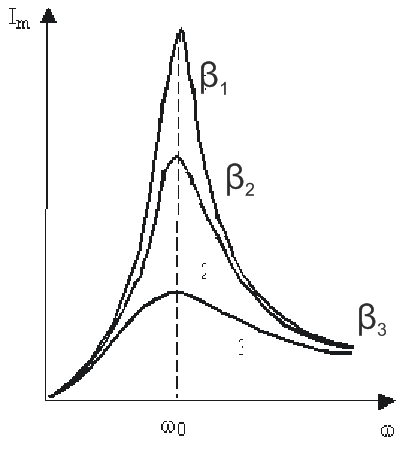
![]()
![]() (резонанс
зарядов)
(резонанс
зарядов)
![]()
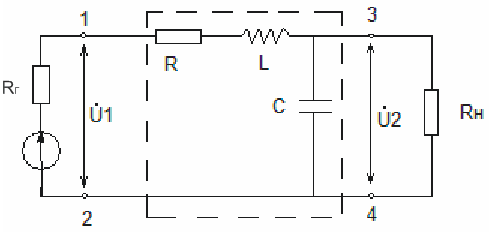
Одиночный последовательный колебательный контур
Подключим последовательный контур к
источнику ЭДС с внутренним сопротивлением
![]()
![]()
![]()
![]()
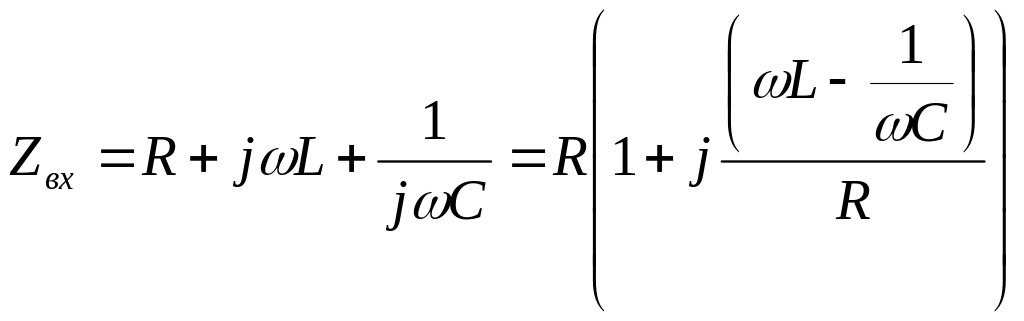
Обозначим расстройку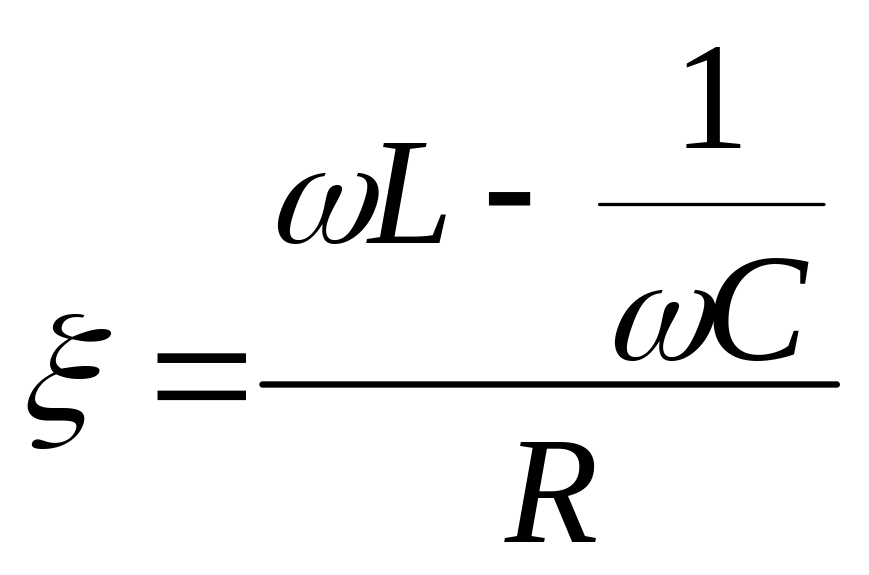 -
обобщенная расстройка.
-
обобщенная расстройка.
Связь между расстройкой и добротностью
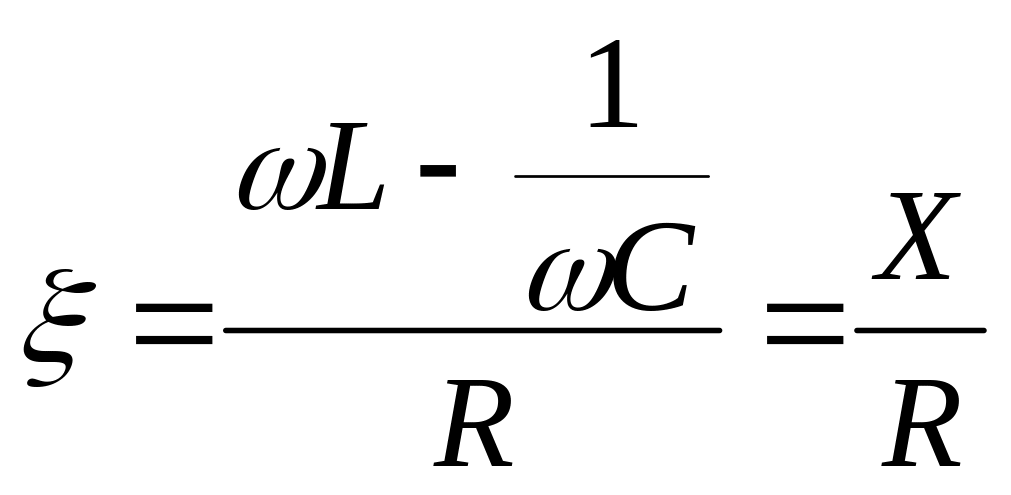
Добротность
![]()
Декремент затухания
![]()
При малых расстройках:![]()
![]()
Добротность:
![]() (1)
(1)
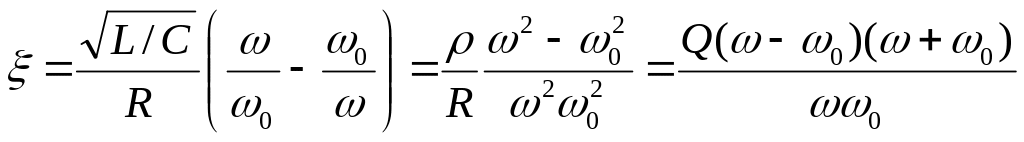
![]() (2)
(2)
![]()
Определим коэффициент передачи.
![]()
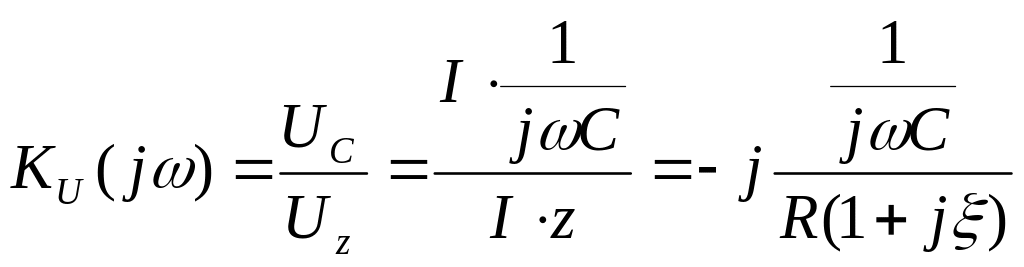 (4)
(4)
![]() умножаем
на волновое сопротивление.
умножаем
на волновое сопротивление.
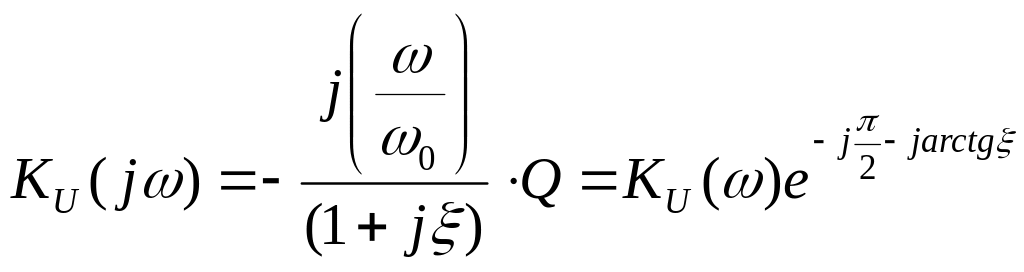
Перейдем к модулю
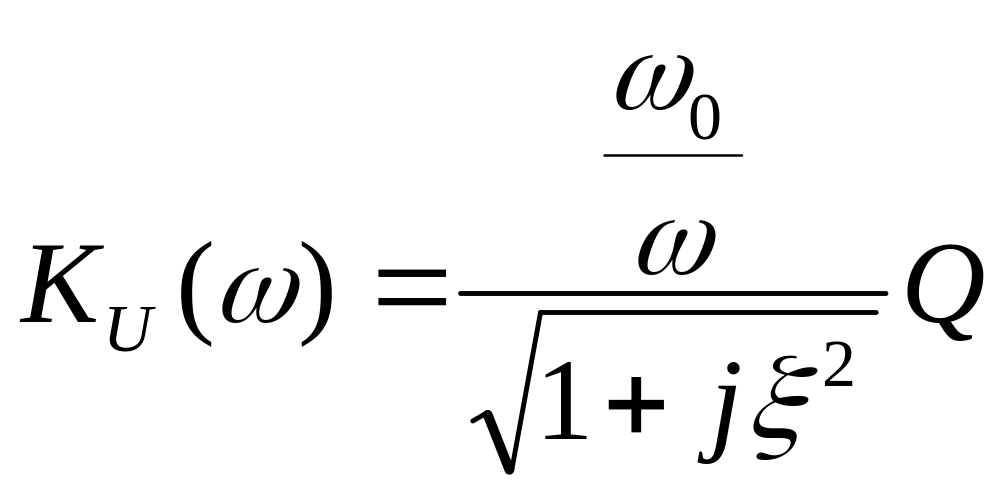 -
АЧХ
-
АЧХ
![]() -
ФЧХ
-
ФЧХ
Т.к. ток в последовательном контуре течет через сопротивление индуктивность и емкость, то резонанс называется резонансом напряжений.
При резонансе напряжений:
![]()
Процессы в контуре часто характеризуют
резонансной кривой, т.е. зависимость
![]() или
или
![]() .
.
Иногда вводят понятие обобщенных резонансных кривых.
![]()
![]()
Если
![]() (обычно
(обычно
![]() ).
).
Параллельный колебательный контур
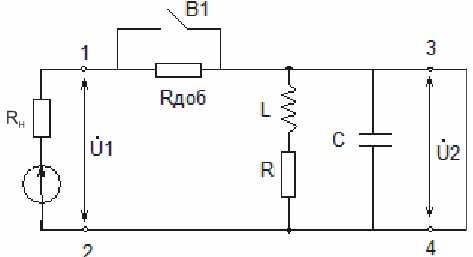
Рассмотрим первый случай, когда
переключение замкнут.
![]() -
дополнительное сопротивление.
-
дополнительное сопротивление.
1.
![]() переключатель замкнут
переключатель замкнут
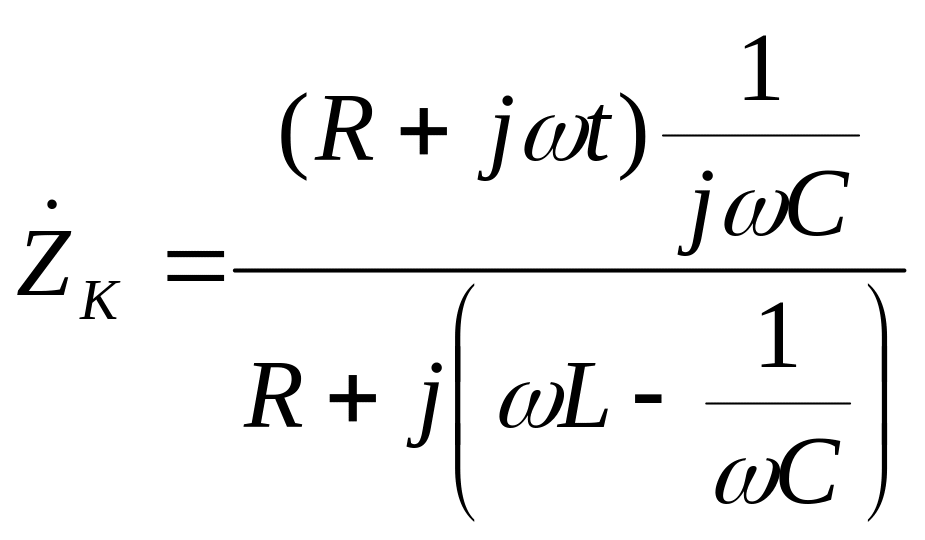
![]()
![]()
![]()
В этом случае сопротивлением в числителе можно пренебречь по сравнению с индуктивным сопротивлением:
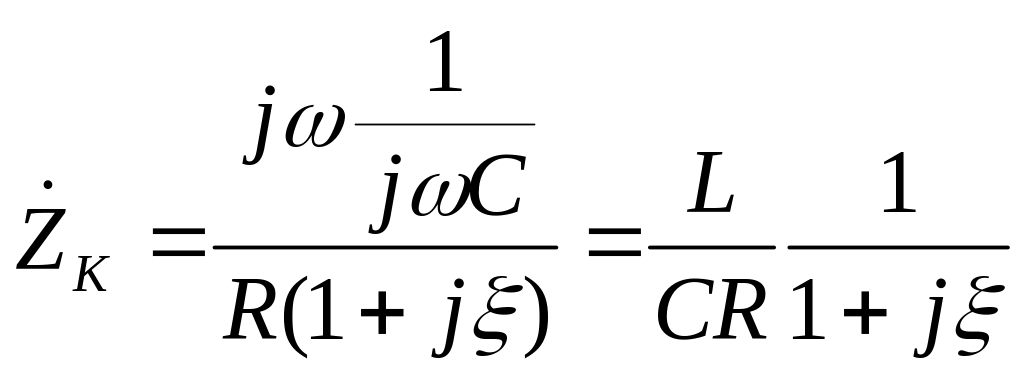 (5)
(5)
Обозначим
![]() (6)
(6)
Т.к. индуктивность и емкость соединены
последовательно, то падение напряжения
на контуре равно напряжению на генераторе,
следовательно коэффициент передачи по
отражению равен единице:
![]() ,
следовательно надо коэффициент передачи
определить по току:
,
следовательно надо коэффициент передачи
определить по току:
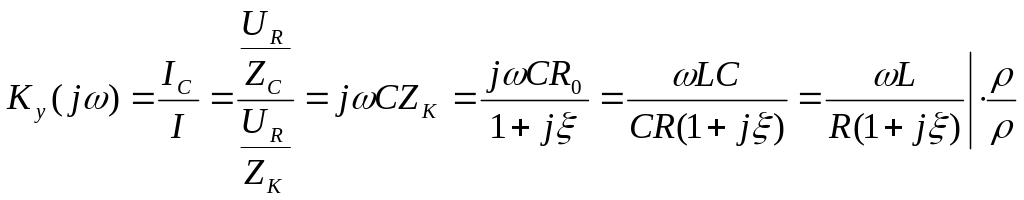
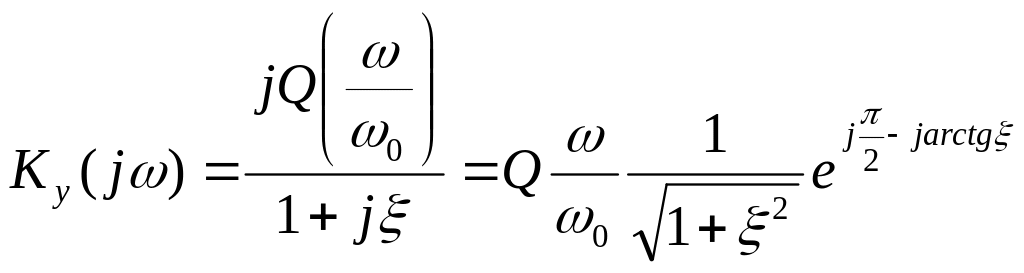
![]() -
АЧХ
-
АЧХ
![]() -
ФЧХ
-
ФЧХ
Обобщенная резонансная кривая:
![]()
![]() при
малых расстройках:
при
малых расстройках:
![]()
В общем случае обобщенная резонансная кривую определяется:
![]() (7)
(7)
Включим добавочное сопротивление. В этом случае сопротивление цепи равно:
![]() (8)
(8)
Коэффициент передачи можно брать по напряжению, т.к. часть напряжения падает на добавочном сопротивлении, следовательно:
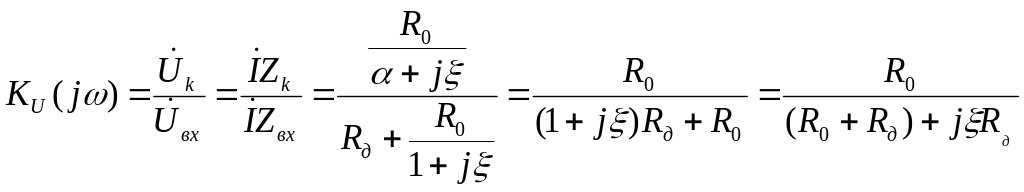 (9)
(9)
Преобразуем к виду:
![]() ,
,
где![]() -
ФЧХ
-
ФЧХ
![]() -
АЧХ
-
АЧХ
Проанализируем (9)
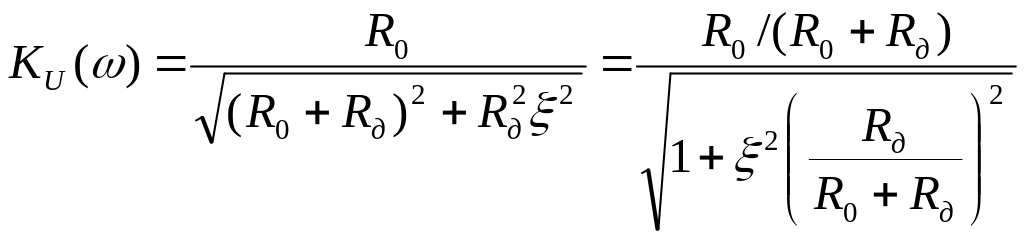
Введем обозначение:
![]()
1. Частный случай.
![]()
![]() -
АЧХ
-
АЧХ
2. Частный случай
![]()
![]() ,
обобщенная кривая имеет вид:
,
обобщенная кривая имеет вид:
![]()
3. Частный случай.
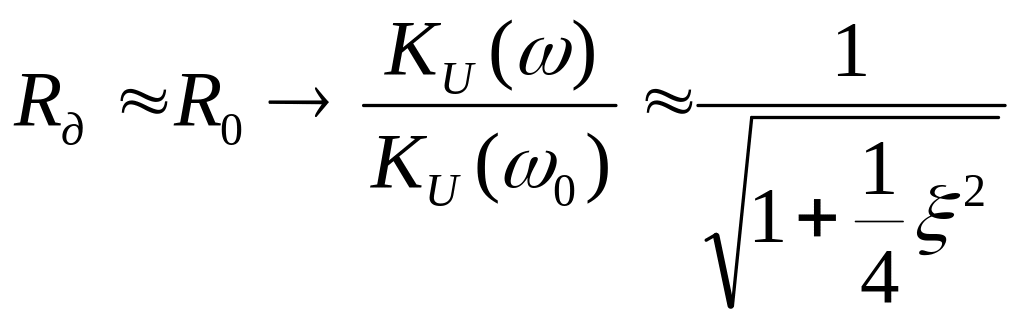
Радиосигналы с амплитудной модуляцией
Модулированные сигналы
Сигналы с телекамер, микрофона и других телеметрических датчиков имеют малую амплитуду и частоту.
Вследствие низкочастотности сигнала, он не может распространяться в пространстве. Чтобы передать информационный низкочастотный сигнал, по радиоканалу, надо перенести его спектр в область спектра с высокой частотой. Такой процесс называется модуляцией.
Процесс осуществляется следующим образом. Пусть имеется передатчик с высокой частотой и он генерирует сигнал:
![]() ,
где
,
где![]() -
параметры, определяющие форму сигнала.
-
параметры, определяющие форму сигнала.
Если любой из параметров
![]() изменяется в зависимости от информационного
сигнала, то несущий сигнал приобретает
новое свойство, он несет в себе информацию
о полезном сигнале. Часто вместо несущего
сигнала берут амплитудный сигнал.
изменяется в зависимости от информационного
сигнала, то несущий сигнал приобретает
новое свойство, он несет в себе информацию
о полезном сигнале. Часто вместо несущего
сигнала берут амплитудный сигнал.
![]()
Параметры:
![]()
Если при двух фиксированных значениях параметров изменяется 3 пропорционально полезному сигналу , то мы будем иметь модулированный сигнал.
Чтобы он повторял информационный сигнал он должен быть линейным.
1.
![]() -
амплитудная модуляция (АМ),
-
амплитудная модуляция (АМ),
![]()
2.
![]() -
частотная модуляция (ЧМ)
-
частотная модуляция (ЧМ)
3.
![]() -
Фазовая модуляция (ФМ)
-
Фазовая модуляция (ФМ)
Т.к. аргумент косинуса зависит от несущей частоты и начальной фазы , то часто частотно-модулированный и фазо-модулированный сигнал называют сигналами с угловой модуляцией. Рассмотрим последовательно все 3 вида модуляции.
1.Амплитудная модуляция.
![]()
![]() (10)
(10)
![]() коэффициент
модуляции, если
не
изменяет знак.
коэффициент
модуляции, если
не
изменяет знак.
Если информационный сигнал
изменяет знак, то вводят коэффициент
модуляции вверх
![]() и
коэффициент модуляции вниз
и
коэффициент модуляции вниз![]()
Коэффициент модуляции определят глубину
модуляции. При малых значениях
![]() ,
будет неглубокая модуляция, при
,
будет неглубокая модуляция, при![]() -
глубокая модуляция, при
-
глубокая модуляция, при
![]() -
перемодуляция.
-
перемодуляция.
![]()
![]()
При неглубокой модуляции мощность передатчика используется частично, следовательно такая модуляция неэффективна.
При глубокой модуляции
![]() ,
амплитуда модулированного сигнала
будет в 2 раза больше, чем амплитуда
несущего сигнала, что приводит к
перегрузке передатчика и, следовательно,
к нелинейным искажениям.
,
амплитуда модулированного сигнала
будет в 2 раза больше, чем амплитуда
несущего сигнала, что приводит к
перегрузке передатчика и, следовательно,
к нелинейным искажениям.
Спектры однотональных и сложных амплитудно-модулированных сигналов
Однотональная модуляция
Пусть полезный сигнал изменяется по гармоническому закону:
![]() (10)
(10)
![]()
![]()
![]()
![]()
Амплитудная модуляция содержит 3
гармоники с частотами
![]() .
.
![]() -
верхняя боковая частота (ВБЧ), колебания
с верхней боковой частотой
-
верхняя боковая частота (ВБЧ), колебания
с верхней боковой частотой
![]() -
нижняя боковая частота (НБЧ).
-
нижняя боковая частота (НБЧ).
Энергетические характеристики амплитудно-моделированного сигнала
![]() (1)
(1)
Амплитудно модулированный сигнал можно представить в виде суммы трех ЭДС.
Подключим в амплитудно модулированному
сигналу сопротивление
![]() Ом
Ом
Эквивалентная схема:
Мощность, выделяемая на сопротивлении:
![]()
(лб - левая боковая, пб - правая боковая)
Как правило, измеряется средняя мощность.
Средняя мощность
![]()
Все взаимные мощности будут равны 0.
![]()
![]()
![]()
Средняя мощность
![]()
![]()
![]()
Для мощности, приходящееся на боковые частоты:
![]() (2)
(2)
Т.е. на полезный сигнал боковыми частотами
даже при глубокой модуляции приходится
![]() .
.
Это означает, что в лучшем случае генератор несущей частоты будет загружен на половину (50%), и следовательно, его мощность будет использоваться неэффективно.
Амплитудная модуляция при сложном моделирующем сигнале (многотональном)
Однотональные модуляции используются редко. В общем случае модулирующий сигнал имеет сложную форму.
Пусть сигнал периодический. Разложим сигнал в ряд Фурье.
![]()
Тогда модулирующий сигнал представляется в виде:
![]() (3)
(3)
Введем парциальный коэффициент модуляции:
![]()
![]() (4)
(4)
Преобразуем произведение косинусов аналогично преобразованию однотональной модуляции, мы получим спектр сигнала:
![]() (5)
(5)
Из (5) следует, что спектр амплитудно
модулированного сигнала содержит
несущую частоту и
колебаний с левой боковой частотой
![]() и
с правой боковой частотой
и
с правой боковой частотой
![]() .
.
Рассмотрим граничный спектральный анализ сигнала.
Спектр модулирующего сигнала
![]()
Спектр модулированного сигнала симметричен относительно частоты и содержит сигналы с левой боковой и правой боковой частотой
![]()
Спектр симметричен относительно частоты
.
Ширина спектра равна
![]() или
или![]() .
.
Балансная и однополосная модуляция
Балансная амплитудная модуляция
Оценка распределения мощностей между несущим сигналом и сигналом с левой и правой боковой частотой показывают, что мощность передатчика используется только максимум на 50%.
Информация, как правило, заключена в колебаниях с левой и правой боковыми частотами. Значит, для повышения эффективности передатчика, нужно подавать колебания с несущей частотой в амплитудно модулированном сигнале. Такая модуляция называется балансной модуляцией.
Сигнал балансной модуляции имеет вид:
![]()
Преобразуя произведение косинусов, получим:
![]() (5)
(5)
Сумма этих двух колебаний с одинаковой амплитудами называются биениями.
![]()
Сигналы, модулированные с одной боковой частотой (ОБП)
Дальнейшее усовершенствование процессов модуляции может быть совершено за счет подавления одной из боковых частот - это является частным случаем обычной модуляции.
Тогда сигнал
![]() (6)
(6)
![]()
![]()
Колебания с подавленной левой боковой
частотой сдвинуть друг относительно
друга по несущей частоте на угол
![]() .
.
Любые колебания модно представить в векторном виде:
![]()
Представим разность колебаний в векторном виде:
![]()
![]()
![]()
Огибающая высокочастотного сигнала. Нарисуем графики зависимости:
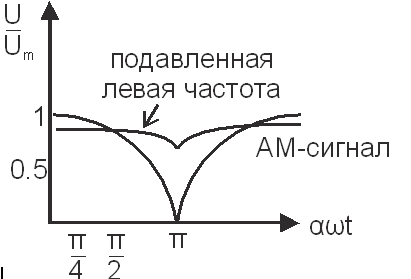
При демодуляции сигнал с подавленной левой боковой частотой воспроизводится с помехами.
Аналогично получаем для многотонального сигнала. Несмотря на преимущества, балансная модуляция не находит широкое применение из-за сложной приборной реализации.
Радиосигналы с угловой модуляцией (основные определения)
Сигналы с угловой модуляцией
При угловой модуляции изменяется фаза
сигнала, пропорционально информационному
сигналу в соответствие с этим модуляция
фазы приводит к сигналам с угловой
модуляцией. Различают частотно-модулируемые
и фазо-модулированные сигналы. Формально
эти процессы похожи, но отличаются
зависимостью частоты
![]() от
амплитуды и частоты модулирующего
сигнала.
от
амплитуды и частоты модулирующего
сигнала.
Рассмотрим фазовую модуляцию. При ней амплитуда сигнала остается.
![]()
![]() (7)
(7)
Из (7) следует, что при изменении сигнала
,
скорость изменения фазы будет больше
чем скорость изменения сигнала. В
некоторый момент времени
достигает
максимума. Максимальный сдвиг фазы
относительно несущего колебания будет
достигать максимума, следовательно
величина
![]() называется
девиацией фазы
называется
девиацией фазы
![]() .
.
Изменяя знак, вводят понятие девиации
фазы вверх![]() и
вниз
и
вниз![]() .
.
![]()
![]()
При фазовой модуляции фаза изменяется
пропорционально модулированному
сигналу.
![]() (8)
(8)
При угловой модуляции вектор колебания
имеет одинаковую амплитуду
![]() и вращается с переменной скоростью,
т.к. угол зависит нелинейным образом.
и вращается с переменной скоростью,
т.к. угол зависит нелинейным образом.
![]()
Рассмотрим частотную модуляцию
![]() -
частотно-модулированный сигнал.
-
частотно-модулированный сигнал.
![]() -
девиация частоты
-
девиация частоты
Определим фазу при частотной модуляции.
Фаза
![]() (10)
(10)
Сопоставляя уравнение (8) и (10) видим, что фазо-модулированный и частотно-модулированный сигнал по форме похожи друг на друга. Разница между этими сигналами заключается в том, что при фазовой модуляции фаза изменяется пропорционально полезному сигналу, при частотной модуляции фаза пропорциональная интегралу от полученного сигнала.
![]() (3)
(3)
Частотно-модулированные колебания. Фазомодулированные колебания
Спектр частотно-модулированного сигнала при малых индексах модуляции
При
![]() .
Разложим
в
ряд Тейлора.
.
Разложим
в
ряд Тейлора.
![]() (7)
(7)
Если
![]() ,
то
,
то
![]()
![]()
Тогда частотно-модулированный сигнал:
![]()
![]()
![]() (8)
(8)
Спектр частотно-модулированного сигнала
содержит 3 частоты: несущую частоту
,
правую боковую
![]() и
левую
и
левую
![]() боковую
частоты.
боковую
частоты.
Сопоставим данный сигнал с амплитудно-модулированным сигналом.
Выражения будут подобны, если вместо
индекса модуляции поставить коэффициент
модуляции
![]() .
Разница заключается в том, что при
частотной модуляции колебание с нижней
боковой частотой имеет знак минус, с
физической точки зрения это значит, что
сигнал нижней боковой частоты сдвинут
по фазе относительно сигнала с верхней
боковой частотой на угол
.
Разница заключается в том, что при
частотной модуляции колебание с нижней
боковой частотой имеет знак минус, с
физической точки зрения это значит, что
сигнал нижней боковой частоты сдвинут
по фазе относительно сигнала с верхней
боковой частотой на угол
![]() .
.
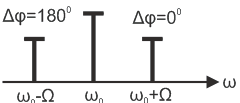
Уточним спектральный состав сигнала, учитывая в разложениях и 2 слагаемых, т.е.:
![]() (9)
(9)
![]()
![]() (10)
(10)
Из данного выражения действует, что спектр имеет 7 составляющих, расположенных симметрично относительно частоты .
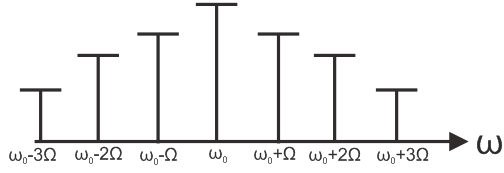
Из (10) следует, что амплитуда несущего колебания с ростом индекса модуляции будет уменьшаться, как амплитуда боковых частот будет расти с ростом индексов модуляции, что ведет к перераспределению сигналов с боковой частотой и несущем колебанием.
Для фазо-модулированного тоже самое.
Частотно-модулированный сигнал при произвольных индексах модуляции
Пусть принимает произвольные значения, тогда частотная модуляция:
![]() (11)
(11)
В математике широко используют функцию Бесселя.
![]() - функция Бесселя
-го
порядка.
- функция Бесселя
-го
порядка.
Данная функция Бесселя является решением
системы уравнений
![]() второго
порядка.
второго
порядка.
![]()
Основным свойством функции Бесселя является:
![]()
Если функция нечетная,
![]()
Если четная,
![]()
Можно показать, что любую экспоненциальную функцию с комплексным показателем можно разложить по функциям Бесселя:
![]()
Заменим
![]()
![]()
![]() (12)
(12)
Выражение (12) определяет частотно-модулированный сигнал при произвольных индексах модуляции. Функция Бесселя определяет амплитуду гармоник. В данном случае нижних и верхних боковых частот будет бесконечное множество.
Чем больше индекс модуляции, тем шире область, в пределах которой функция Бесселя изменяется незначительно. Индекс модуляции можно подобрать так, чтобы амплитуда несущего колебания будет равна нулю.
![]() ,
колебания отсутствуют.
,
колебания отсутствуют.
Уравнение![]() имеет
решение
имеет
решение
![]()
Корни уравнения находятся по таблицам.
Как правило, в реальных случаях ряд
ограничивают по числу членов ряда, при
этом отбрасывается все слагаемые с
номером
![]() .
.
Практическая ширина спектра
![]()
Для больших уровней индекса модуляции
(![]() )
равен
)
равен
![]() .
.
Сигналы с угловой модуляцией обладают большой полосой частот, в связи с этим для передачи таких сигналов нужна высокая частоты (метровый и дециметровый диапазоны). Расширение полосы сигнала приводит к уменьшению шумов и следовательно, к большей помехоустойчивости сигналов к помехам.
Спектр колебаний при гармонической угловой модуляции
Ортогональные сигналы с угловой модуляцией
Процессы при угловой модуляции значительно сложнее, чем при амплитудной модуляции. В связи с этим рассмотрим только однотональную модуляцию.
Сигнал:
![]()
Исследуем частотно-модулированный сигнал.
![]()
![]()
Величина
![]() называется
индексом угловой модуляции. При таком
обозначении:
называется
индексом угловой модуляции. При таком
обозначении:
![]() (4)
(4)
Из равенства (4) следует, что индекс модуляции представляет собой девиацию фазы.
![]()
Девиация фазы при фазовой модуляции зависит только от амплитуды модулирующего сигнала, и не зависит от его частоты.
Девиация фазы (индекс модуляции) при частотной модуляции зависит от амплитуды модулирующего сигнал и от его частоты.
![]()
Сигнал с частотной модуляцией представим в виде:
![]() (5)
(5)
Аналогично с фазовой модуляцией.
Предположим,
![]()
![]()
![]() (6)
(6)
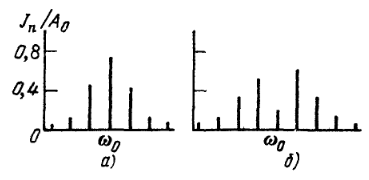
Спектры колебания
при угловой модуляции: а)
![]() 6)
6)
![]() .
.
Уравнение параметра сигнала
Процесс переноса полезного сигнала в области низких частот, в область высоких частот называется модуляцией.
![]()
Надо иметь передатчик, который создает высокочастотные колебания
Если амплитуда сигнала изменяется пропорционально сигналу, такой сигнал называется амплитудно-модулированным сигналом.
![]()
Если частота сигнала равна
![]() ,
получим частотную модуляцию.
,
получим частотную модуляцию.
Если фаза меняется, получим фазовую
модуляцию![]() .
.
При идеальной модуляции законы изменения амплитуды и фазы не изменяются, т.к. нет искажений данных параметров.
Представим модулирующий сигнал в виде узкополосного процесса.
![]()
Модулирующий сигнал
![]() -
модулированный сигнал.
-
модулированный сигнал.
Сопоставляя выражения для модулированного
и модулирующего сигнала, видим, что
![]() -
закон изменяя огибающей и фазы не
меняются, видим что изменяется лишь
частота гармонического заполнения
-
закон изменяя огибающей и фазы не
меняются, видим что изменяется лишь
частота гармонического заполнения
![]() .
Если законы огибающей не изменяется,
то корреляционной функции и модулирующего
сигналов не изменяется по форме и
отличаются только частотой.
.
Если законы огибающей не изменяется,
то корреляционной функции и модулирующего
сигналов не изменяется по форме и
отличаются только частотой.
Спектральной плотности сигнала также
не изменяется по форме. Отличие заключается
в том, что спектр модулирующего сигнала
смещается в область частоты
![]() .
.
Реальная модуляция сопровождается нелинейными искажениями, искажениями фазы и уменьшением полосы частот. В этом случае ширина полосы модулирующего сигнала будет больше полосы частот модулирующего сигнала. Искажение амплитуды и фазы приводят к изменениям формы корреляционной функции и спектральной плоскости.
Кроме того, изменяются законы изменения амплитуды и фазы. Если модулирующий сигнал представляет собой случайный стационарный процесса, а несущие колебания гармонический процесс, то модулированный сигнал будет случайным нестационарным процессом и его корреляционные характеристики, а также спектральные плоскости зависят от конкретного момента времени.
Для определения спектральных и частотных характеристик применяют операционное усреднение.
![]()
Виды модуляции
Исследования видов модуляции необходимо для определения свойств радиоканала, уменьшения избыточного модулированного сигнала, улучшение режима работы передатчика, для определения потенциальной помехоустойчивости радиоканалов, помех в соседнем сигнале и успешном решении задач электромагнитной совместимости.
Для определения корреляционной функции спектральной плотности законов изменения огибающей и фазы модулированного сигнала и сигнала переносчика, а также корреляционной функции и спектральной неоднородностей модулирующего сигнала передатчика.
Для классификации видов модуляции вводят следующие признаки сигнала:
1. Характер сигнала: детерминированный сигнал, случайный стационарный процесс, случайный нестационарный процесс
2. Характер сигнала: аналоговый, дискретный
3. Характер информационного сигнала: амплитуда, период, фаза, частота, длительность
Введем классы модулирующих сигналов:
А - детерминированный непрерывнозначный процесс.
B - детерминированные дискретные последовательности.
С - случайный стационарный непрерывнозначный процесс.
D - случайная стационарная последовательность.
E - случайный нестационарный непрерывнозначный процесс.
F - случайная нестационарная последовательность.
G - дискретная случайная стационарная последовательность
Для переносчиков вводятся классы 1,2..
Корреляционные и спектральные характеристики модулированного сигнала
В ряде случаев модулированный сигнал можно представить в виде узкополосого сигнала
![]() (1).
(1).
Вычислим корреляционную функцию для непрерывных видов модуляции. Для остальных видов модуляции корреляционная функция определяется аналогичным образом:
![]()
![]()
Косинус преобразуем в виде экспоненты:
![]()
Учитывая последнюю форму, получим:
![]()
Перемножим экспоненты, получим 4 интеграла:
Амплитуды
![]() изменяются
значительно медленнее, чем
изменяются
значительно медленнее, чем
![]() и
и
![]() ,
эти величины можно вынести за знак
интеграла. Эти величины можно вынести
за занак интеграла.
,
эти величины можно вынести за знак
интеграла. Эти величины можно вынести
за занак интеграла.
![]()
Второй интеграл тоже равен нулю.
Преобразуя остальные 2 интеграла и учитывая формулу Эйлера, получаем:
![]()
![]() (2)
- позволяет определить корреляционную
функцию
для
узкополосного модулирующего сигнала.
(2)
- позволяет определить корреляционную
функцию
для
узкополосного модулирующего сигнала.
В качестве примера вычисление спектральной
функции рассмотрим балансную модуляцию
в случае нестационарного сигнала
![]() гармонического
сигнала с амплитудой, равной 1.
гармонического
сигнала с амплитудой, равной 1.
![]()
Балансно-модулированный сигнал
![]() (3)
(3)
Предположим, что случайный стационарный процесс определяется:
![]()
![]()
По определению интеграл
![]() (4)
(4)
Таким образом, чтобы получить корреляционную
функцию балансно-модулированного
сигнала, надо умножить коэффициент
высокочастотного заполнения на
корреляционную функцию случайного
нестационарного процесса
![]()
Спектральную плотность балансно-модулированного сигнала определим на основе преобразования Фурье.
![]()
![]()
Разбивая интеграл на 2 интеграла:
![]()
Вычисляя значения интеграла с учетом модуля , мы можем получить следующее выражение для спектральной функции:
![]() (5)
(5)
Спектральная плотность содержит 2
круговые частоты
![]() и
и
![]() ,
причем боковые частоты:
,
причем боковые частоты:
![]() (5)
(5)
Создадим аналитический сигнал
![]()
Аналитический сигнал
![]() имеет спектр в области только положительных
частот и его спектральная функция:
имеет спектр в области только положительных
частот и его спектральная функция:
![]()
![]() (6)
(6)
Определим ширину спектра модулированного сигнала:
![]()
Вводя длину
![]() и
вычисляя интеграл
и
вычисляя интеграл
![]() :
:
![]()
Таким образом, ширина спектра модулированного сигнала совпадает с шириной спектра модулирующего случайного нестационарного сигнала (см. телеграфный сигнал).
После преобразований, можно сделать вывод: корреляционная функция определяется в виде интеграла, в котором учитывается зависимость амплитуда прямого и задержанного сигнала, а также законы изменения фаз прямого и задержанного сигнала.
Задавая значение
и![]() ,
,![]() ,
,![]() ,
можем определить спектральную функцию
модулированного сигнала. Из прямого
преобразования Хинчина-Винера можем
спектральную плотность модулированного
сигнала.
,
можем определить спектральную функцию
модулированного сигнала. Из прямого
преобразования Хинчина-Винера можем
спектральную плотность модулированного
сигнала.
Определение линейной цепи. Дельта функция - как пример пробного сигнала. Свойства дельта-функции.
Методы исследования прохождения сигнала через пассивные линейные цепи
Любая радиотехническая цепь (электронная) преобразует сигнал и ее входе и на выходной сигнал. Из данного свойства цепи следует математическая модель цепи:
![]() (7)
(7)
Коэффициент называют оператором цепи. Свойства любой цепи зависит от фундаментальных свойств оператора . Сформулируем основные свойства цепи:
1. Если оператор цепи не зависит от амплитуды входного сигнала, то такая цепь называется линейной. Для линейной цепи всегда выполняется принцип суперпозиции:
![]() (6)
(6)
Линейные цепи содержат сопротивления, емкости и индуктивности, а также активные элементы (транзисторы).
2. Если смещение на входе цепи во времени
входного сигнала определяет такое же
смещение в выходном сигнале, то цепи
называется стационарной. В этом случае
![]() ,
,
![]()
Дельта-функция как пример пробного сигнала
Для определения свойств цепи используют
сигналы, обладающие определенными
характеристиками. такие сигналы называют
пробными сигналами. В качестве пробного
сигнала используется дельта-функция
Дирака, которая равна 0, если
![]()
![]()
![]()
Дельта-функцию в частности, можно определить прямоугольным импульсом
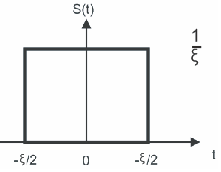
Площадь импульса
![]()
![]()
![]()
Для дельта-функции применяются свойства
фильтрации
![]()
![]()
Существует ряд аналитических представлений -функции:
![]() (8)
(8)
![]()
![]() (в
формуле (8))
(в
формуле (8))
Вычислим спектральную плотность дельта-функции. Использующие фильтрующие функции для дельта-функции:
![]()
Т.е. спектральная плотность дельта-функции не зависит от частоты и является постоянной.
![]()
Из выражение следует симметричность и :
![]()
![]()
![]()
Временной метод анализа передачи сигналов через линейные цепи. Импульсная и спектральная характеристики сигналов.
Методы исследования процессов прохождения сигналов через линейные цепи
Используется фильтрующие свойства дельта-функции, получаем входной сигнал:
![]() (9)
(9)
Из (9) следует, что входной сигнал можно
представить как предельную сумму
-импульсов,
смещенных относительно друг друга на
величину
.
Амплитуда таких импульсов является
значением входных сигналов в моменты
времени
![]()
![]()
Такой метод называется методом интеграла наложения, т.е. на последовательность дельта-импульсов накладывается полезный сигнал. Если известен отклик системы на пробный импульс (дельта-импульс), то, суммируя все отклики в цепи, определим выходной сигнал (отклик всей системы) на любой сложный сигнал. В связи с этим вводятся понятие импульсной характеристики, которая является откликом системы на дельта-импульс
Отклик системы:![]() либо
либо
![]()
![]()
Отклик системы
или
![]() называется импульсной характеристикой
цепи. Импульсная характеристика вместе
с интегральным наложением позволяет
определить все основные свойства цепи
(частотный коэффициент передачи и т.д.).
называется импульсной характеристикой
цепи. Импульсная характеристика вместе
с интегральным наложением позволяет
определить все основные свойства цепи
(частотный коэффициент передачи и т.д.).
Выходной сигнал определяется как:
![]()
Учитывая, что
![]()
![]() (10)
(10)
Из (10) следует, что выходной сигнал
представляет собой сумму входных
сигналов с весовым множителем
![]()
С целью упрощения дальнейших преобразований
делаем замену переменных
![]()
![]()
Преобразуем функцию, используя преобразование Фурье
![]()
Можно сделать замену
![]()
![]()
![]() -
частотный коэффициент передачи (частотная
характеристика)
-
частотный коэффициент передачи (частотная
характеристика)
![]()
Спектральный метод анализа передачи сигналов через линейные цепи
В основе метода лежит использование
передаточной функции цепи
![]() .
Если на входе линейного четырехполюсника
действует сигнал произвольной формы в
виде ЭДС
.
Если на входе линейного четырехполюсника
действует сигнал произвольной формы в
виде ЭДС
![]() ,
то, применяя спектральный метод, следует
определить спектральную плотность
входного сигнала
,
то, применяя спектральный метод, следует
определить спектральную плотность
входного сигнала
![]() .
Эта операция легко осуществляется с
помощью выражения
.
Эта операция легко осуществляется с
помощью выражения
![]() .
Умножением
на
определяется спектральная плотность
сигнала на выходе четырехполюсника.
Наконец, применение к произведению
.
Умножением
на
определяется спектральная плотность
сигнала на выходе четырехполюсника.
Наконец, применение к произведению
![]() обратного преобразования Фурье определяет
выходной сигнал в виде функции времени.
обратного преобразования Фурье определяет
выходной сигнал в виде функции времени.
Если входной сигнал записан в виде интеграла.
![]()
то выходной сигнал можно представить в аналогичной форме:
![]()
Сравнение выражений показывает, что
сигнал на выходе линейной цепи можно
получить суммированием составляющих
спектра
![]() входного сигнала, взятых с весом
.
Иными словами, передаточная функция
цепи
является весовой функцией, определяющей
относительный вклад различных составляющих
спектра
в сигнал
.
входного сигнала, взятых с весом
.
Иными словами, передаточная функция
цепи
является весовой функцией, определяющей
относительный вклад различных составляющих
спектра
в сигнал
.
Анализ переходных процессов упрощается
при представлении как внешнего
воздействия, так и передаточной функции
в виде преобразований Лапласа. При этом
обозначение передаточной функции
можно сохранить прежним, а изменить
только аргумент, так что
перейдет в
![]() .
Функция же
переходит в
.
Функция же
переходит в
![]() .
Преобразование Лапласа от функции
времени
в дальнейшем обозначается символом
.
Преобразование Лапласа от функции
времени
в дальнейшем обозначается символом
![]() .
При этом выражение приводится к виду
.
При этом выражение приводится к виду
![]()
При
![]() замкнутый контур интегрирования,
образованный добавлением дуги бесконечно
большого радиуса в левой полуплоскости,
охватывает все полюсы подынтегральных
функций как
,
так и
,
благодаря чему имеет место соотношение:
замкнутый контур интегрирования,
образованный добавлением дуги бесконечно
большого радиуса в левой полуплоскости,
охватывает все полюсы подынтегральных
функций как
,
так и
,
благодаря чему имеет место соотношение:
![]() (здесь
(здесь
![]() —
сумма вычетов в указанных полюсах).
—
сумма вычетов в указанных полюсах).
При
![]() контур интегрирования лежит в правой
полуплоскости, не содержит полюсов и
интеграл равен нулю.
контур интегрирования лежит в правой
полуплоскости, не содержит полюсов и
интеграл равен нулю.
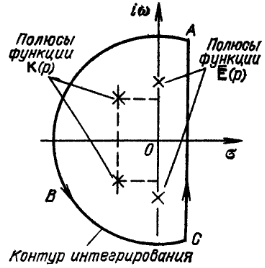
Показанное на рис. расположение полюсов
функции
(на мнимой оси) соответствует ЭДС
вида
![]() ,
существующей при
,
существующей при
![]() .
.
Итак вычисление интеграла сводится к определению вычетов в полюсах подынтегральной функции. Представим подынтегральную функцию в виде
![]()
Знаменатель
![]() образуется
произведением множителей вида
образуется
произведением множителей вида
![]() где
где
![]() — полюсы не только функции
— полюсы не только функции
![]() ,
но и функции
,
но и функции
![]() .
.
Тогда вычет функции
![]() ,
имеющей в точке
,
имеющей в точке
![]() простой
полюс (первой кратности), определится
формулой
простой
полюс (первой кратности), определится
формулой
![]()
Если функция имеет в точке полюс кратности ( — целое положительное число), то:
![]()
Особенности анализа процесса прохождения радиосигналов через избирательные цепи
При решении задач о прохождении сигналов через электрические цепи основное внимание уделяют изменениям информационных параметров сигналов, поскольку это связано с проблемой сохранения информации, переносимой сигналами. В случаях, когда информация заложена непосредственно в форме сигнала (случай простых сигналов) задача сохранения информации сводится к задаче сохранения формы (или спектра) сигнала.
Иначе дело обстоит с радиосигналом, в котором информация заключена в одном из нескольких параметров высокочастотного колебания. Не обязательно сохранять полностью структуру этого колебания; достаточно лишь сохранить закон изменения того параметра, в котором заключена информация. Так, в случае амплитудно-модулированного колебания, важно передать огибающую амплитуд, а некоторое изменение частоты или несущее колебание, не имеющее существенного значения, при анализе можно не учитывать. При передаче радиосигналов с угловой модуляцией, наоборот, основное внимание следует уделить точному воспроизведению закона изменения частоты и фазы, а изменением амплитуды можно пренебречь.
Эти особенности радиосигналов открывают путь к некоторому упрощению методов анализа их передачи через линейные цепи. Возможность упрощения особенно существенна, когда радиосигнал представляет собой узкополосный процесс, а цепь - узкополосную систему. Это как раз и характерно для реальных радиосигналов и реальных радиоцепей.
а) Приближенный спектральный метод.
Пусть цепь представляет собой избирательную
систему, передаточная функция
![]() которой имеет максимум вблизи частот
которой имеет максимум вблизи частот
![]() и
и
![]() .
И пусть на ее входе действует высокочастотное
модулированное колебание
спектральная характеристика которого
имеет два максимума вблизи частот
.
И пусть на ее входе действует высокочастотное
модулированное колебание
спектральная характеристика которого
имеет два максимума вблизи частот
![]() и
и
![]() .
В общем случае резонансная частота цепи
не совпадает с центральной частотой
сигнала
.
В общем случае резонансная частота цепи
не совпадает с центральной частотой
сигнала
![]() ,
т.е. имеет место расстройка
,
т.е. имеет место расстройка
![]() (20)
(20)
которая является величиной того же порядка, что и полоса пропускания цепи.
Составим выражение для сигнала на выходе
цепи. Если входной сигнал имеет
гармоническое заполнение, т.е.
![]() ,
то выкладки значительно упрощаются при
использовании понятия аналитического
сигнала:
,
то выкладки значительно упрощаются при
использовании понятия аналитического
сигнала:
![]() (21)
(21)
Спектральная функция этого сигнала
![]() существует только в области положительных
частот, поэтому при определении
аналитического сигнала на выходе цепи
следует исходить из выражения:
существует только в области положительных
частот, поэтому при определении
аналитического сигнала на выходе цепи
следует исходить из выражения:
![]() (22)
(22)
Спектральные функции высокочастотного
модулированного колебания
![]() и аналитического сигнала
и аналитического сигнала
![]() при
при
![]() связаны соотношением
связаны соотношением
![]() ,
причем при
,
причем при
![]() ,
где
,
где
![]() ‑
спектральная функция огибающей.
‑
спектральная функция огибающей.
Следовательно
![]() .
.
Подставляя это выражение в (22), получаем
![]() (23)
(23)
Введем переменную
![]() .
Тогда
.
Тогда
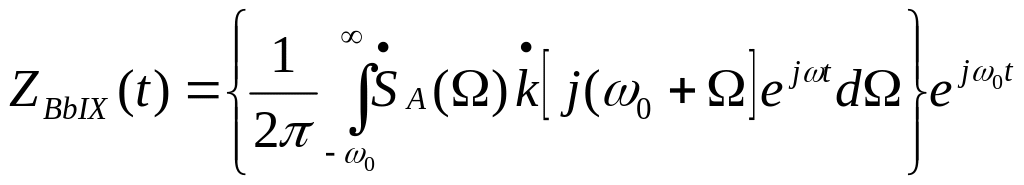 (24)
(24)
Из сопоставления (24) с (21) видно, что выражение, стоящее в фигурных скобках соответствует комплексной огибающей выходного колебания:
Дальнейшее упрощение анализа вытекает
из свойств передаточной функции
резонансных цепей, обладающих сильно
выраженной частотной избирательностью:
Модуль коэффициента передачи
![]() быстро убывает при удалении
от резонансной частоты. Поэтому
передаточную функцию целесообразно
выражать в виде функции расстройки
частоты относительно
резонансной частоты
:
быстро убывает при удалении
от резонансной частоты. Поэтому
передаточную функцию целесообразно
выражать в виде функции расстройки
частоты относительно
резонансной частоты
:
![]() (26)
(26)
где постоянный параметр расстройки
.
Т.к. при
![]() ,
,
![]() ,
нижний предел интегрирования в (25) можно
заменить на
,
нижний предел интегрирования в (25) можно
заменить на
![]() .
При этом оно принимает вид :
.
При этом оно принимает вид :
![]() (27)
(27)
Это выражение ничем не отличается от
обычного интеграла Фурье, определяющего
оригинал по заданной спектральной
плотности огибающей
![]() и передаточной функции
и передаточной функции
![]() .
.
Заменив
![]() на
на![]() ,
получим выражение в форме обратного
преобразования Лапласа :
,
получим выражение в форме обратного
преобразования Лапласа :
![]() (28)
(28)
Таким образом, анализ передачи
узкополосного высокочастотного колебания
через избирательную цепь по существу
сводится к анализу изменений, претерпеваемых
комплексной огибающей входного сигнала.
После нахождения
![]() и
и
![]() для выходного аналитического сигнала
можно будет написать следующее выражение
:
для выходного аналитического сигнала
можно будет написать следующее выражение
:
![]() (29)
(29)
откуда
![]() (30)
(30)
Вычисления, связанные с определением
![]() по формуле (28), значительно проще, чем
при непосредственном определении
по формуле (28), значительно проще, чем
при непосредственном определении
![]() с
помощью обратного преобразования
Лапласа, так как переход от
к
с
помощью обратного преобразования
Лапласа, так как переход от
к
![]() и от
и от
![]() к
к
![]() сокращает число особых точек подынтегральной
функции.
сокращает число особых точек подынтегральной
функции.
б) Упрощенный метод интеграла наложения. (Метод огибающей).
Упрощение спектрального метода было
достигнуто упрощением передаточной
функции избирательной цепи
![]() .
Аналогично метод интеграла наложения
можно упростить укорочением импульсной
характеристики
,
тесно связанной с передаточной функцией
.
.
Аналогично метод интеграла наложения
можно упростить укорочением импульсной
характеристики
,
тесно связанной с передаточной функцией
.
Основываясь на общем выражении
![]()
и переходя к аналитической функции
![]() ,
соответствующей физической функции
,
находим:
,
соответствующей физической функции
,
находим:
![]() (31)
(31)
Заменим переменную
![]() .
Тогда с учетом формулы (26) и после замены
нижнего предела
.
Тогда с учетом формулы (26) и после замены
нижнего предела
![]() на
получим
на
получим
![]()
С другой стороны, представив искомую импульсную характеристику в виде узкополосной функции:
![]()
имеем :
![]() (33)
(33)
Из сравнения (32) и (33) непосредственно вытекает равенство, определяющее комплексную огибающую импульсной характеристики :
![]() (34)
(34)
Применение этого выражения упрощает вычисление импульсной характеристики .
Обратимся теперь к (27). Используя правило,
согласно которому произведению двух
спектров
![]() соответствует функция времени
,
являющаяся сверткой функций
и
:
соответствует функция времени
,
являющаяся сверткой функций
и
:
![]() ,
(35)
,
(35)
где
![]() -
временной интервал, в течении которого
одновременно существуют функции
и
,
из (27) можем определить
в виде свертки двух функций времени,
соответствующих спектральным функциям
и
.
Первой из этих функций соответствует
-
временной интервал, в течении которого
одновременно существуют функции
и
,
из (27) можем определить
в виде свертки двух функций времени,
соответствующих спектральным функциям
и
.
Первой из этих функций соответствует
![]() ,
а второй, как это следует из (34) -
,
а второй, как это следует из (34) -
![]() .
Следовательно
.
Следовательно
![]() (36)
(36)
Это выражение является общим, пригодным
для любых избирательных цепей и любых
узкополосных сигналов. В тех случаях,
когда свободные колебания характеризуются
постоянной частотой заполнения, как,
например, в одиночном колебательном
контуре,
![]() вырождается в постоянную фазу и выражение
(36) существенно упрощается. То же самое
относится и к сигналам с немодулированной
частотой заполнения, когда
вырождается в постоянную фазу и выражение
(36) существенно упрощается. То же самое
относится и к сигналам с немодулированной
частотой заполнения, когда
![]() обращается
в постоянную величину.
обращается
в постоянную величину.
Метод интеграла наложения эффективен в тех случаях, когда временные характеристики сигналов или цепей ( или тех и других) оказываются более простыми, чем спектральные. Такое положение имеет место , например, при анализе прохождения ЧМ сигналов.
Матричный метод анализа свойств пассивного четырёхполюсника
Кроме методов, основанных на определении импульсных и переходных характеристик, для анализа свойств линейных цепей широко применяют матричный метод. Его использование основывается на том, что для описания свойств сколь угодно сложной цепи достаточно знать зависимость между ее внешними напряжениями и токами. В этом случае сложная цепь заменяется эквивалентным четырехполюсником. Такой четырехполюсник эквивалентен данной цепи в том смысле, что токи и напряжения на его внешних зажимах тоже равны соответствующим значениям в реальной цепи.
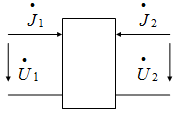
Между входными и выходными комплексными амплитудами токов и напряжений может быть установлена зависимость в виде системы двух уравнений. Максимальное число пар уравнений равно шести. Из них наиболее употребимы четыре.
1. Если в качестве независимых переменных
выбраны токи
![]() и
и
![]() ,
то их связь с
,
то их связь с
![]() и
и
![]() устанавливается парой уравнений
устанавливается парой уравнений
![]() (1)
(1)
В матричной форме:![]() (2)
(2)
Элементы матрицы называются
![]() -параметрами.
Положим, что они являются полными
сопротивлениями холостого хода
четырехполюсника. На основании (1) можем
записать :
-параметрами.
Положим, что они являются полными
сопротивлениями холостого хода
четырехполюсника. На основании (1) можем
записать :
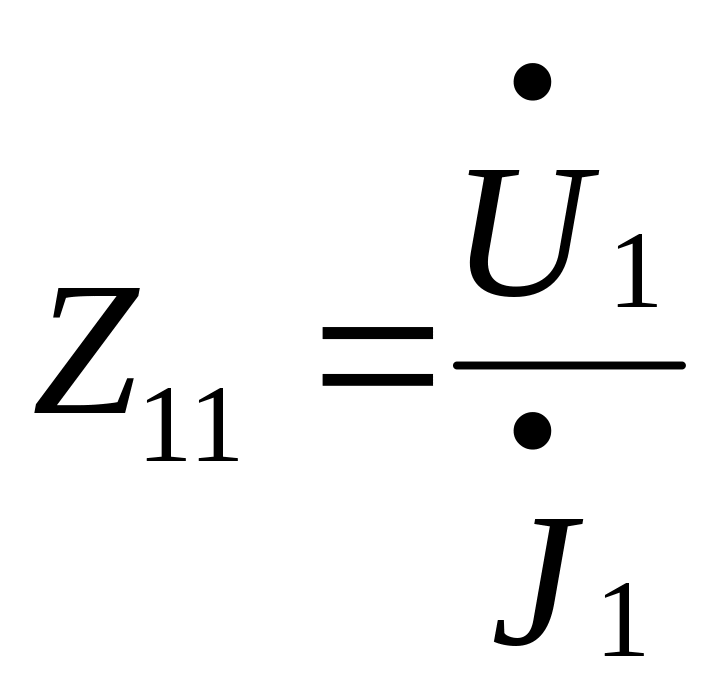 ,
при
,
при
![]() ;
;
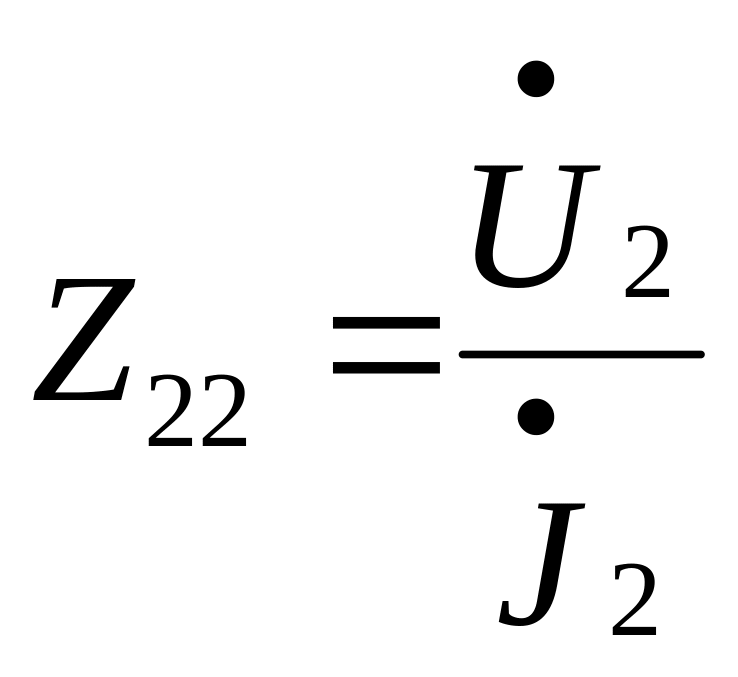 ,
при
,
при
![]() ;
;
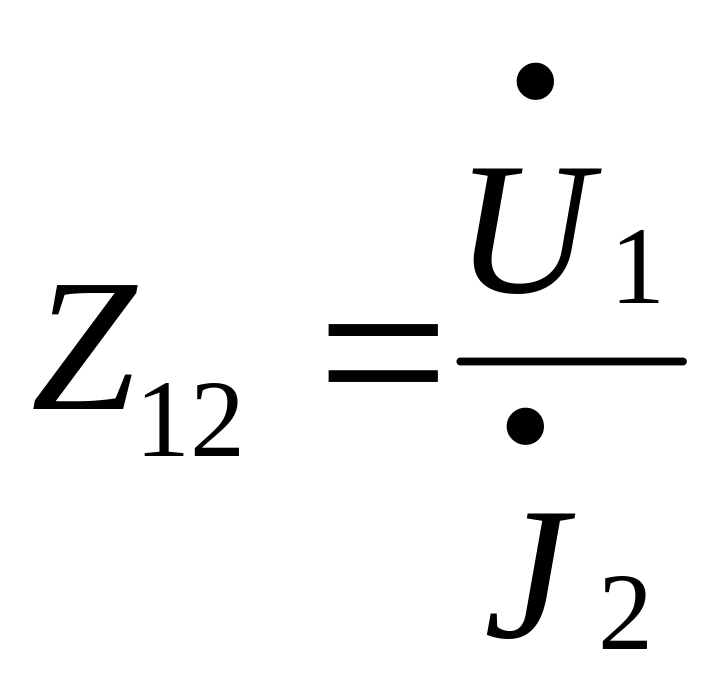 ,
при
;
,
при
;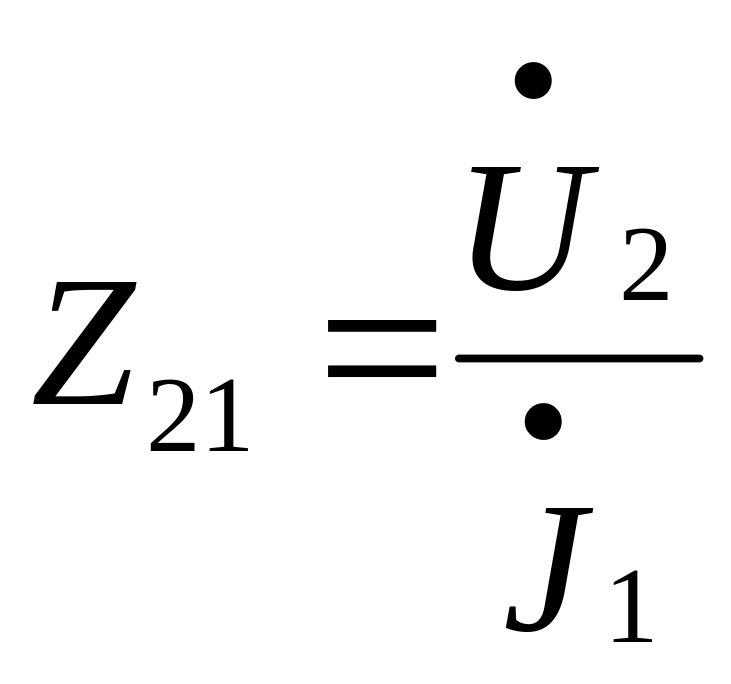 ,
при
,
при
Отсюда следует, что
![]() - входное сопротивление четырехполюсника
при разомкнутом выходе (“холостой
ход”);
- входное сопротивление четырехполюсника
при разомкнутом выходе (“холостой
ход”);
![]() - выходное сопротивление четырехполюсника
при разомкнутом входе ;
- выходное сопротивление четырехполюсника
при разомкнутом входе ;
![]() - сопротивление передачи от входа к
выходу при разомкнутом входе ;
- сопротивление передачи от входа к
выходу при разомкнутом входе ;
![]() - сопротивление передачи от выхода к
входу при разомкнутом выходе.
- сопротивление передачи от выхода к
входу при разомкнутом выходе.
Среди четырехполюсников часто встречаются
взаимные (обратимые), для которых
![]() .
Если четырехполюсник обладает симметрией,
то
.
Если четырехполюсник обладает симметрией,
то
![]() .
Таким образом, обратимый симметричный
четырехполюсник имеет два независимых
-параметра:
.
Таким образом, обратимый симметричный
четырехполюсник имеет два независимых
-параметра:
![]() .
.
2. Если в качестве независимых переменных
выбраны напряжения
и
, то связь с токами
и
![]() устанавливается с помощью матрицы
проводимостей :
устанавливается с помощью матрицы
проводимостей :
![]() (2)
(2)
Коэффициенты матрицы (![]() -параметры)
являются полными проводимостями
короткого замыкания четырехполюсника.
При коротком замыкании входа
-параметры)
являются полными проводимостями
короткого замыкания четырехполюсника.
При коротком замыкании входа
![]() ,
при K3 выхода -
,
при K3 выхода -
![]() .
Подставляя поочередно эти условия в
(2), находим, что
.
Подставляя поочередно эти условия в
(2), находим, что
![]() и
и
![]() - входная и выходная проводимости:
- входная и выходная проводимости:
![]() - проводимости передачи при K3 выхода
или входа.
- проводимости передачи при K3 выхода
или входа.
3. Матрица
![]() ‑параметров
связывает напряжение на входе и ток на
выходе (
‑параметров
связывает напряжение на входе и ток на
выходе (
![]() )
с током на входе и напряжением на выходе
(
)
с током на входе и напряжением на выходе
(![]() )
:
)
:
![]() (3)
(3)
В режиме ХХ на входе и K3 на выходе из (3) найдем :
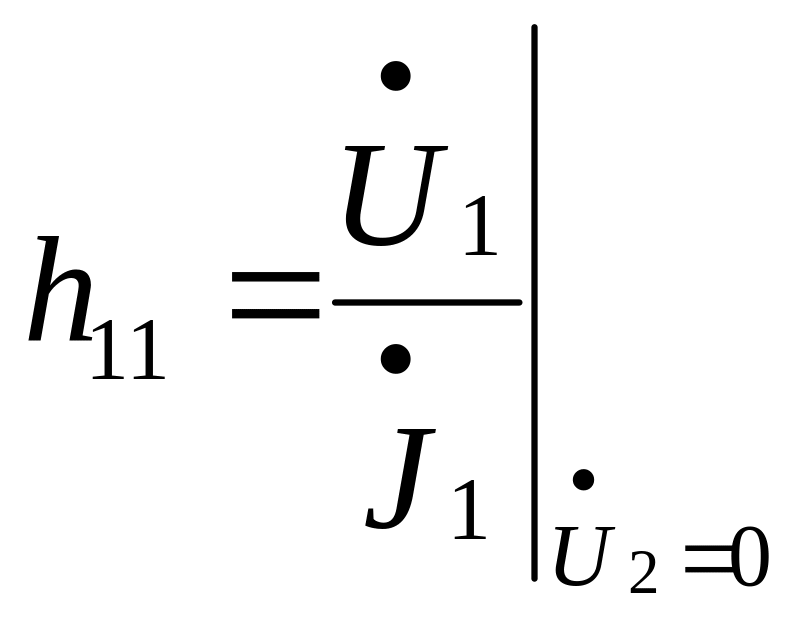 -
полное входное сопротивление
четырехполюсника при К3 выхода;
-
полное входное сопротивление
четырехполюсника при К3 выхода;
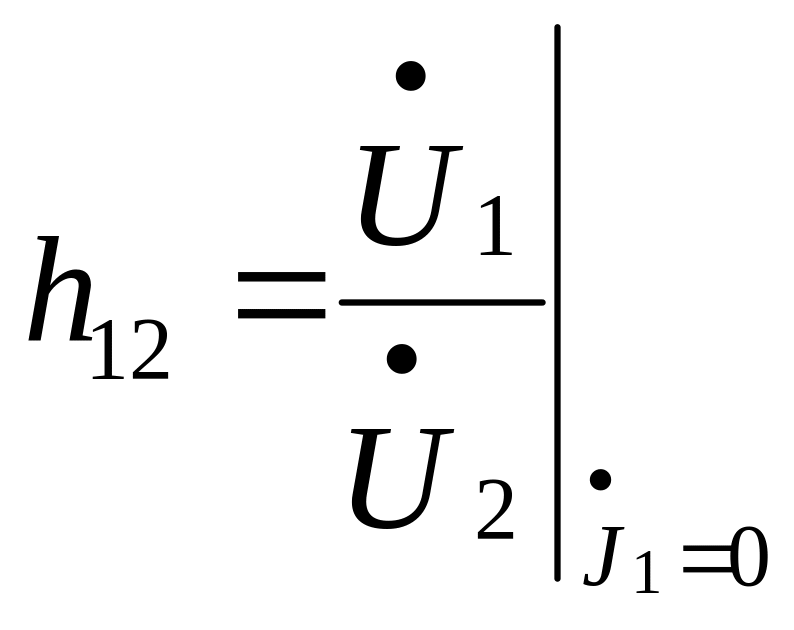 -
обратный коэффициент передачи по
напряжению (от выхода по входу) при ХХ
на входе ;
-
обратный коэффициент передачи по
напряжению (от выхода по входу) при ХХ
на входе ;
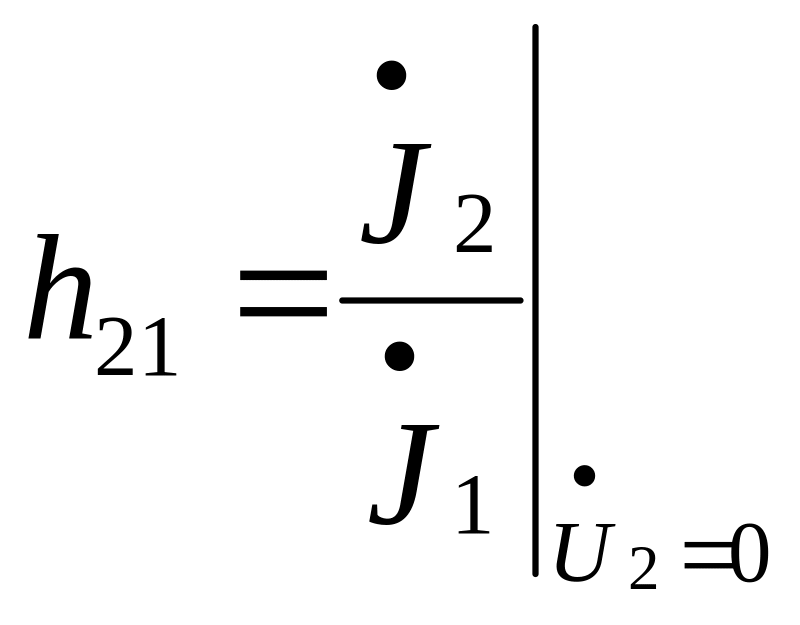 -
коэффициент передачи по току (от входа
к выходу) при К3 выхода ;
-
коэффициент передачи по току (от входа
к выходу) при К3 выхода ;
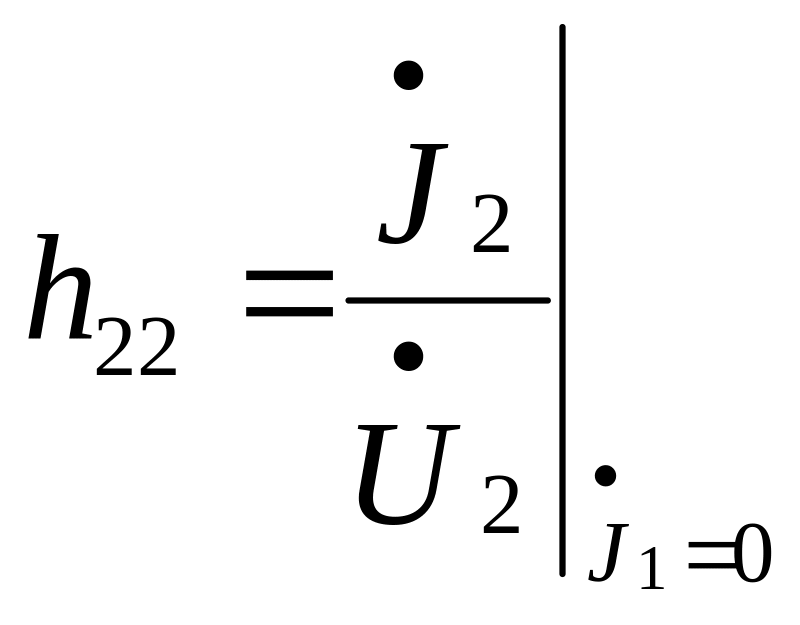 -
выходная проводимость при ХХ на входе.
-
выходная проводимость при ХХ на входе.
4. Матрица передачи (![]() -матрица)
связывает входные ток и напряжение (
-матрица)
связывает входные ток и напряжение (![]() )
с выходными током и напряжением (
)
с выходными током и напряжением (![]() ).
Но при использовании
-матрицы
изменяют направление выходного тока
на противоположное для удобства.
).
Но при использовании
-матрицы
изменяют направление выходного тока
на противоположное для удобства.
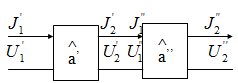
В соответствии с определением -матрицы имеем :
![]() (4)
(4)
Элементы -матрицы определяются из (4) при ХХ и К3 на выходе :
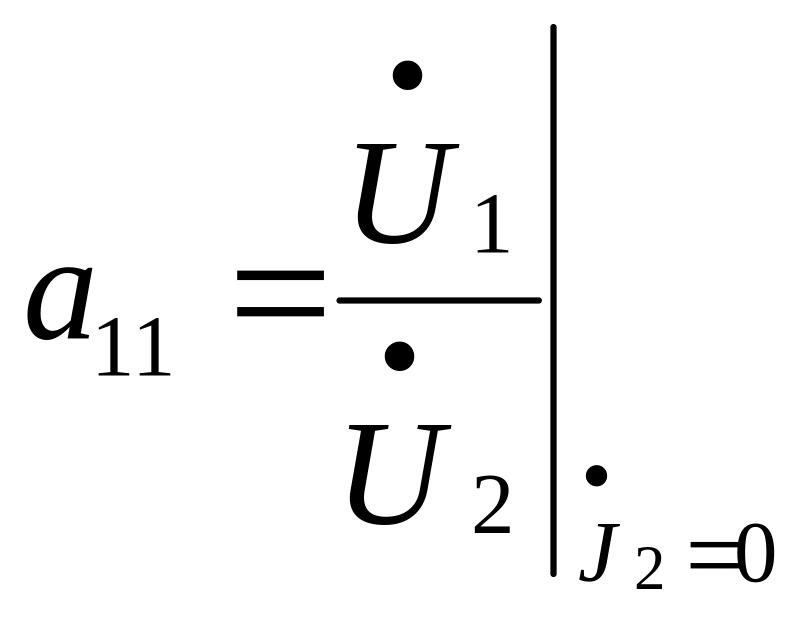 -
обратный коэффициент передачи по
напряжению при ХХ на выходе;
-
обратный коэффициент передачи по
напряжению при ХХ на выходе;
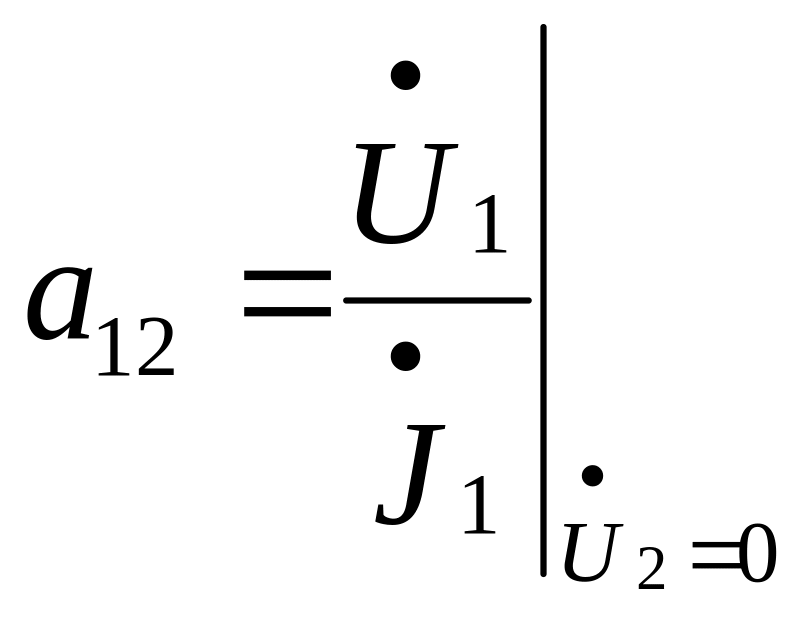 -
сопротивление передачи от входа к выходу
при К3 выхода ;
-
сопротивление передачи от входа к выходу
при К3 выхода ;
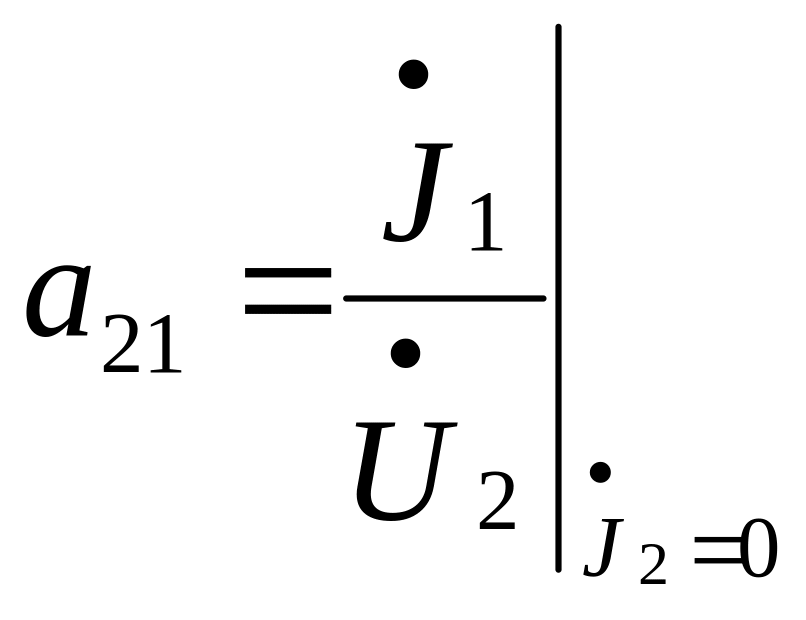 -
проводимость передачи от входа к выходу
при К3 выхода ;
-
проводимость передачи от входа к выходу
при К3 выхода ;
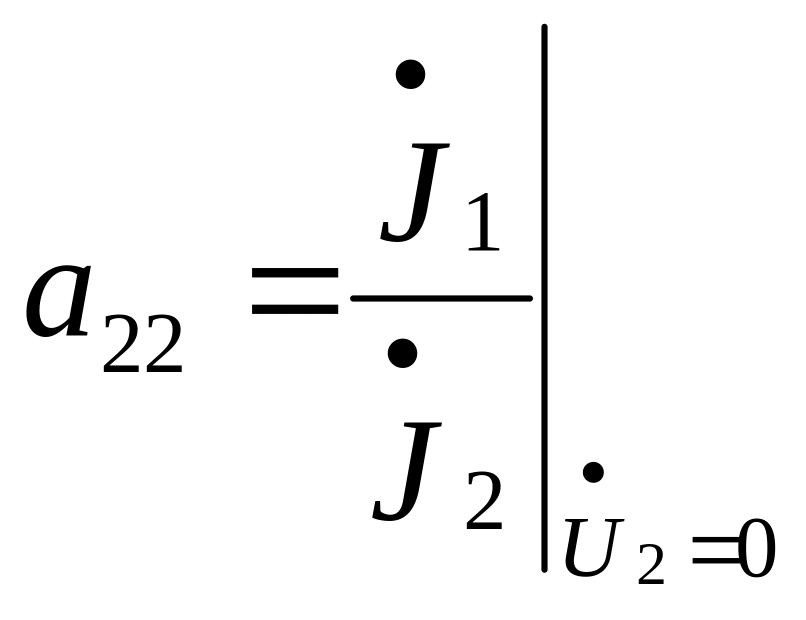 -обратный
коэффициент передачи по току при К3
выхода.
-обратный
коэффициент передачи по току при К3
выхода.
Определитель
-матрицы
взаимного четырехполюсника (
)
![]() .
.
Т.к. один и тот же четырехполюсник может
быть описан любой из рассмотренных
матриц (системой параметров), то между
соответствующими параметрами существует
простая дробно - линейная связь. Например,
элементы
![]() -матрицы
и
-матрицы
и
![]() -матрицы
связаны соотношениями :
-матрицы
связаны соотношениями :
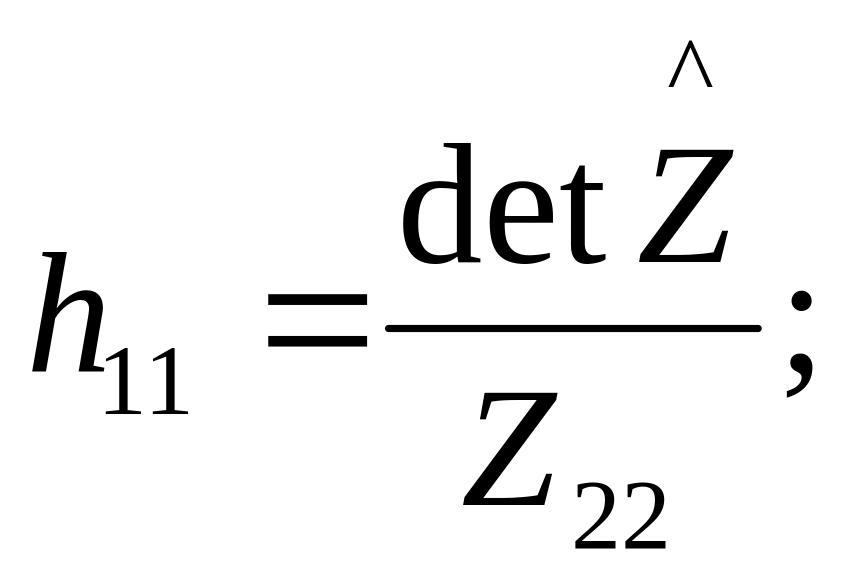
![]()
![]()
![]() (5)
(5)
Эквивалентные схемы пассивных четырёхполюсников
Так как четырехполюсник характеризуется только тремя неизвестными величинами, то простейшая схема замещения четырехполюсника должна содержать 3 элемента. На рисунке эквивалентные схемы Т-образная и П-образная

Выразим
![]() и
и
![]() через
через
![]() и
и
![]() для T-образной эквивалентной
схемы и сопоставим эти выражения с
уравнениями четырехполюсника, записанными
в форме А
для T-образной эквивалентной
схемы и сопоставим эти выражения с
уравнениями четырехполюсника, записанными
в форме А
![]() ,
,
следовательно
![]()
Отсюда связь между параметрами четырехполюсника и его эквивалентной Т-образной схемой.
![]()
Аналогично для П-образной эквивалентной схемы
![]()
и следовательно
![]()
Отсюда связь между параметрами четырехполюсника и его П-образной эквивалентной схемы.
![]()
Для симметричного четырехполюсника
![]() и соответственно в эквивалентных схемах:
и соответственно в эквивалентных схемах:
![]()
Характеристики линейных активных четырёхполюсников в системе h - параметров
Матрица ‑параметров связывает напряжение на входе и ток на выходе ( ) с током на входе и напряжением на выходе ( ) :
(3)
В режиме ХХ на входе и K3 на выходе из (3) найдем :
- полное входное сопротивление четырехполюсника при К3 выхода;
- обратный коэффициент передачи по напряжению (от выхода по входу) при ХХ на входе ;
- коэффициент передачи по току (от входа к выходу) при К3 выхода ;
- выходная проводимость при ХХ на входе.
Активной называют цепь, коэффициент
передачи мощности которой больше
единицы. С точки зрения закона сохранения
энергии такое возможно, если в цепи
действует дополнительный источник
энергии, энергия которого преобразуется
в энергию выходного сигнала. Преобразование
осуществляется с помощью транзисторов,
электронных ламп и других элементов,
называемых активными. Эквивалентное
представление цепи определяется режимом
работы активного элемента. Для малых
амплитуд переменного сигнала характеристики
активных элементов практически линейны.
В этом случае активную цепь можно
представить линейным четырехполюсником.
Принято считать, что большинство активных
четырехполюсников невзаимны, то есть
![]() .
.
На входе активных четырехполюсников
действуют источники управляющих
(входных) сигналов, а к выходу подключено
сопротивление нагрузки
![]() .
Под выходным напряжением при этом
подразумевается падение напряжения на
сопротивлении нагрузки. Для удобства
выкладок мы будем считать, что падение
напряжения на нагрузке
.
Под выходным напряжением при этом
подразумевается падение напряжения на
сопротивлении нагрузки. Для удобства
выкладок мы будем считать, что падение
напряжения на нагрузке
![]() равно по значению и противоположно по
знаку напряжению
на выходных зажимах четырехполюсника.
равно по значению и противоположно по
знаку напряжению
на выходных зажимах четырехполюсника.
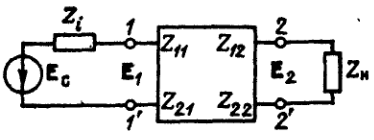
Все основные свойства активных линейных цепей - основные параметры, эффекты обратной связи, критерии устойчивости цепей с обратной связью - мы будем рассматривать на основе ранее изложенной теории линейного четырехполюсника.
Для вывода соотношений, описывающих основные характеристики линейных активных цепей, запишем соотношение (3) линейного четырехполюсника в виде :
![]() (17)
(17)
Соотношение (17) является системой
уравнений контурных токов, в качестве
которых выступают входной и выходной
токи, заданные своими амплитудами. На
рисунке изображена эквивалентная схема
четырехполюсника, построенная в
соответствии с уравнениями (17). В этой
схеме с помощью источника напряжения
![]() учтено влияние напряжения
учтено влияние напряжения
![]() на величину
,
а с помощью источника тока
на величину
,
а с помощью источника тока
![]() - влияние входного тока на ток
.
- влияние входного тока на ток
.
Т.к.
![]() ,
то второе уравнение (17) примет вид
,
то второе уравнение (17) примет вид
![]() ,
откуда для частотного коэффициента
передачи по току
,
откуда для частотного коэффициента
передачи по току
![]() (18), где
(18), где
![]() .
.
Частотный коэффициент передачи по
напряжению
![]() найдем исключив ток
найдем исключив ток
![]() из первого уравнения (17) и использовав
(18) :
из первого уравнения (17) и использовав
(18) :
![]() (19)
(19)
где
![]() .
.
Коэффициенты передачи (18) и (19) можно рассматривать как коэффициенты усиления по току и напряжению активного четырехполюсника.
Входное сопротивление активного четырехполюсника найдем из первого уравнения (17) с учетом (18)
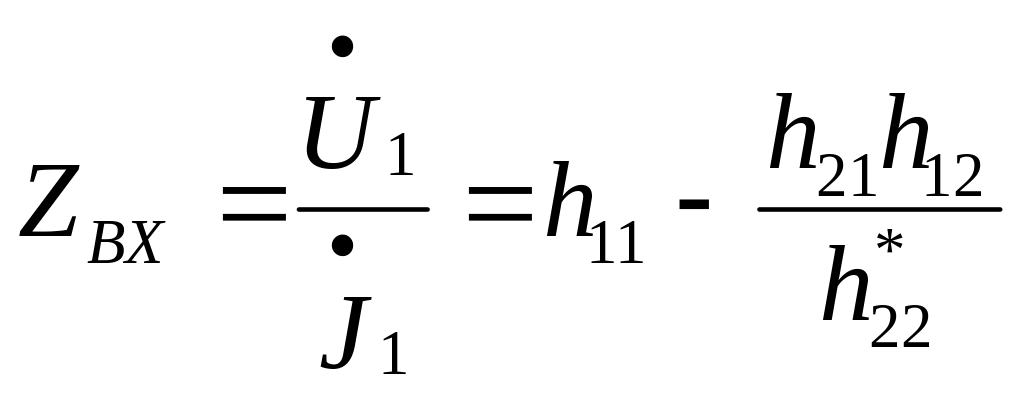 (22)
(22)
Выходное сопротивление
![]() - сопротивление на разомкнутых
выходных зажимах четырехполюсника при
подключенном по входу источнике сигала
с внутренним сопротивлением
- сопротивление на разомкнутых
выходных зажимах четырехполюсника при
подключенном по входу источнике сигала
с внутренним сопротивлением
![]() (т.е. полагая, что
(т.е. полагая, что
![]() )
- найдем из второго уравнения (17)
)
- найдем из второго уравнения (17)
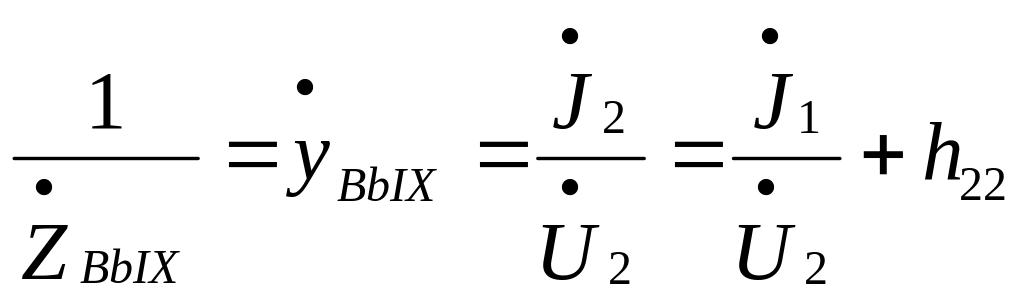
При
![]() ,
,
![]() ,
где
,
где
![]() .
Окончательно для
.
Окончательно для
![]() получаем:
получаем:
![]() (22)
(22)
Полученные соотношения заметно упрощаются
при условии
![]() :
:
![]()
![]()
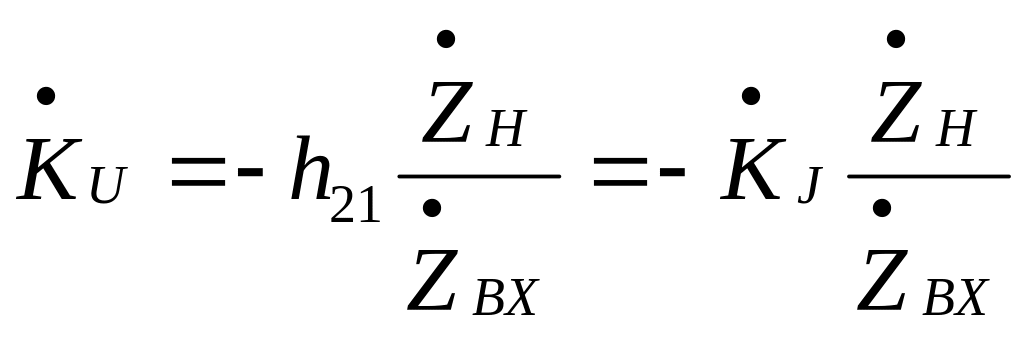 (22)
(22)
Рассмотрим теперь, что представляют
собой h-параметры активного
четырехполюсника. Для этого запишем
первое уравнение системы (17) в виде
функциональной зависимости
![]() .
Используя разложение в ряд Тейлора по
малым приращениям входного тока
.
Используя разложение в ряд Тейлора по
малым приращениям входного тока
![]() и выходного напряжения
и выходного напряжения
![]() ,
найдем вызывающее их приращение входного
напряжения
,
найдем вызывающее их приращение входного
напряжения
![]() ,
в виде
,
в виде
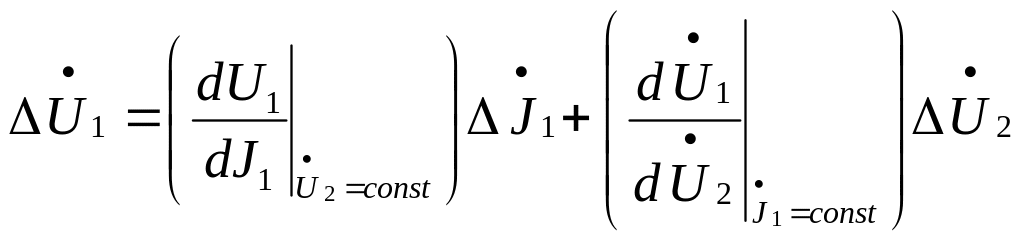
Сравнив полученное соотношение с первым уравнением (17), запишем
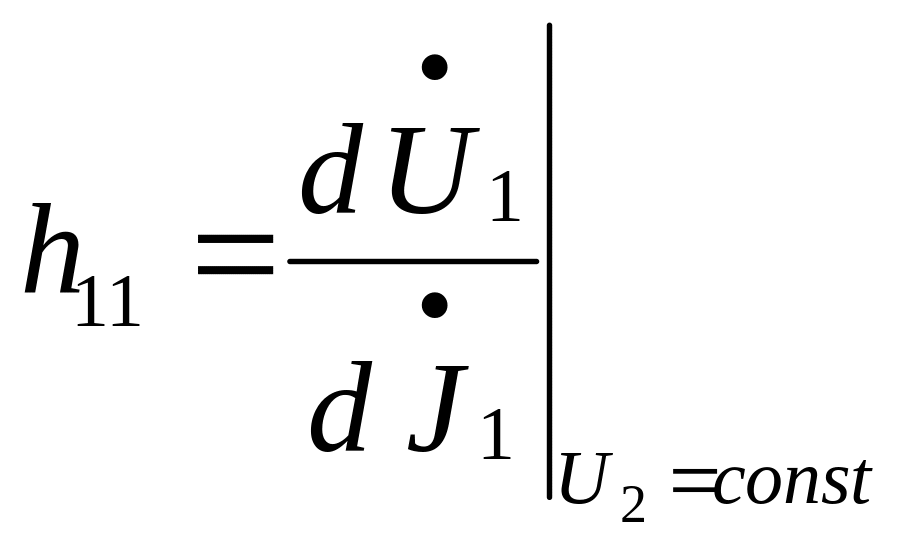 ,
,
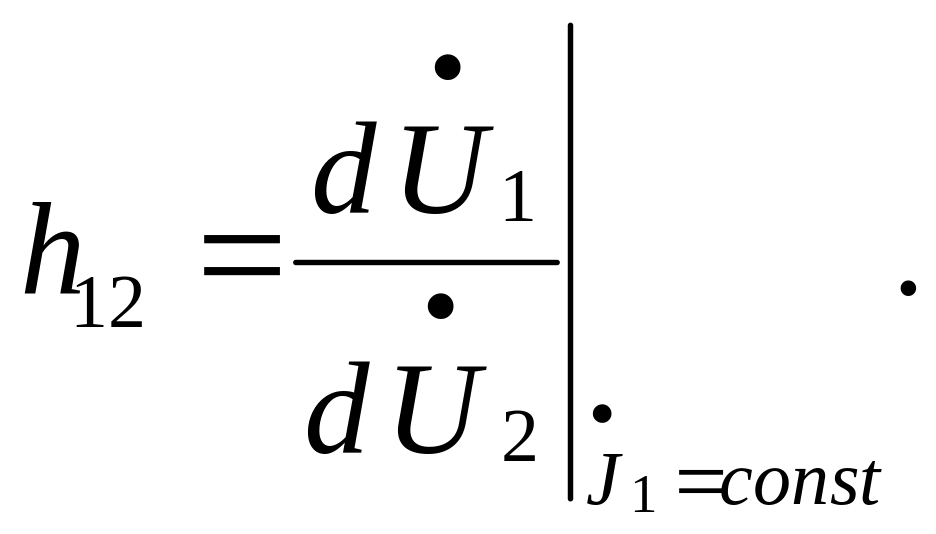 23)
23)
Малыми приращениями являются малые
переменные токи и напряжения. Таким
образом, для малых сигналов параметры
![]() и очевидно,
и очевидно,
![]() являются дифференциальными и представляют
собой наклон характеристик
являются дифференциальными и представляют
собой наклон характеристик
![]() вокруг заданной рабочей точки. Эти
характеристики для активных элементов
не являются линейными, поэтому система
уравнений справедлива, строго говоря,
при исчезающе малой амплитуде входных
воздействий. Тем не менее положение
рабочей точки может быть выбрано таким
образом, что, в довольно широкой области
вблизи нее, характеристики могут
считаться линейными с достаточной
степенью точности. На практике считают,
что h-параметры относятся к переменным
малым напряжениям и токам.
вокруг заданной рабочей точки. Эти
характеристики для активных элементов
не являются линейными, поэтому система
уравнений справедлива, строго говоря,
при исчезающе малой амплитуде входных
воздействий. Тем не менее положение
рабочей точки может быть выбрано таким
образом, что, в довольно широкой области
вблизи нее, характеристики могут
считаться линейными с достаточной
степенью точности. На практике считают,
что h-параметры относятся к переменным
малым напряжениям и токам.
Характеристики линейных активных четырёхполюсников в системе z - параметров
Если в качестве независимых переменных выбраны токи и , то их связь с и устанавливается парой уравнений
(1)
В матричной форме: (2)
Элементы матрицы называются -параметрами. Положим, что они являются полными сопротивлениями холостого хода четырехполюсника. На основании (1) можем записать :
, при ; , при ; , при ; , при
Отсюда следует, что - входное сопротивление четырехполюсника при разомкнутом выходе (“холостой ход”); - выходное сопротивление четырехполюсника при разомкнутом входе ; - сопротивление передачи от входа к выходу при разомкнутом входе ; - сопротивление передачи от выхода к входу при разомкнутом выходе.
Среди четырехполюсников часто встречаются взаимные (обратимые), для которых . Если четырехполюсник обладает симметрией, то . Таким образом, обратимый симметричный четырехполюсник имеет два независимых -параметра: .
Характеристики линейных активных четырёхполюсников в системе z - параметров
Если в качестве независимых переменных выбраны токи и , то их связь с и устанавливается парой уравнений
(1)
В матричной форме: (2)
Элементы матрицы называются -параметрами. Положим, что они являются полными сопротивлениями холостого хода четырехполюсника. На основании (1) можем записать :
, при ; , при ; , при ; , при
Отсюда следует, что - входное сопротивление четырехполюсника при разомкнутом выходе (“холостой ход”); - выходное сопротивление четырехполюсника при разомкнутом входе ; - сопротивление передачи от входа к выходу при разомкнутом входе ; - сопротивление передачи от выхода к входу при разомкнутом выходе.
Среди четырехполюсников часто встречаются взаимные (обратимые), для которых . Если четырехполюсник обладает симметрией, то . Таким образом, обратимый симметричный четырехполюсник имеет два независимых -параметра: .
Транзисторный усилитель как пример активного четырёхполюсника
В широкополосных усилителях, усилительные приборы обеспечивают выполнение неравенств:
![]() ,
где
,
где
![]() -
проводимость
-
проводимость
Поэтому при грубой оценке усилительной способности четырехполюсника можно исходить из приближенных равенств:
![]() (5.20) - коэффициент усиления по напряжению
(5.20) - коэффициент усиления по напряжению
![]() (5.21) - коэффициент усиления по току
(5.21) - коэффициент усиления по току
Отсюда следует, что коэффициент усиления мощности (выраженный в вольтамперах)
![]() (22)
(22)
Здесь заменили связью с другими
параметрами![]()
Очевидна решающая роль параметра
![]() в усилении мощности колебания в активном
четырехполюснике.
в усилении мощности колебания в активном
четырехполюснике.
При анализе активного четырехполюсника как усилителя важное значение имеют такие его параметры, как входное и выходное сопротивления.
Входное сопротивление (между зажимами
1—1`) легко определить с помощью уравнений
![]()
в сочетании с![]() .
.
Подставив
![]() в первое уравнение для
в первое уравнение для
![]() ,
получим:
,
получим:
![]()
откуда
![]() (23)
(23)
Под выходным сопротивлением четырехполюсника
подразумевается сопротивление между
зажимами 2-2' при
![]() (но с учетом внутреннего сопротивления
источника сигнала
(но с учетом внутреннего сопротивления
источника сигнала![]() ).
Сопротивление
рассматривается при этом как нагрузка.
).
Сопротивление
рассматривается при этом как нагрузка.
По аналогии с (5.23) при замене
![]() на
на
![]() и
и
![]() на
на
![]() получаем:
получаем:
![]() (24)
(24)
При учете внутреннего сопротивления
источника
сигнала под коэффициентом усиления
следует подразумевать отношение
![]() - Этот коэффициент можно найти с помощью
формулы
- Этот коэффициент можно найти с помощью
формулы
![]()
добавлением
к
![]() или
или![]() .
Таким образом,
.
Таким образом,
![]() (25
и 26)
(25
и 26)
Выбор наиболее удобной для практики системы параметров зависит от типа усилительного прибора и схемы его включения. Поясним это на примере широко распространенного усилителя на транзисторе, включенном по схеме с общим эмиттером (ОЭ).
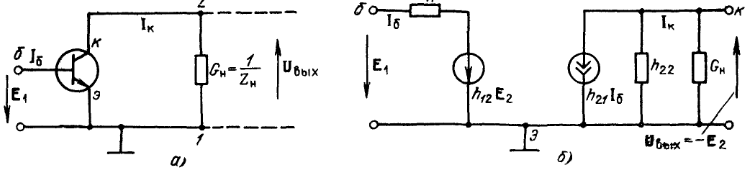
Транзисторный усилитель (а) и его схема замещения (б)
Особенностью работы транзистора в схеме
с ОЭ является управление током коллектора
с помощью воздействия на ток базы. Кроме
того, необходимо учитывать обратное
воздействие выходного напряжения
![]() на входную цепь. Эти свойства
транзистора удобно описываются
уравнениями четырехполюсника. В
связи с этим в теории и технике
транзисторных усилителей общепринята
матрица H-параметров.
на входную цепь. Эти свойства
транзистора удобно описываются
уравнениями четырехполюсника. В
связи с этим в теории и технике
транзисторных усилителей общепринята
матрица H-параметров.
Усилительная способность активного
четырехполюсника в основном определяется
безразмерным параметром
![]() (соответственно
(соответственно
![]() ).
Для усилителя с ОЭ этот параметр
совпадает с отношением токов
).
Для усилителя с ОЭ этот параметр
совпадает с отношением токов
![]() .
Он входит в паспортные данные
биполярного транзистора и обозначается
символом
.
Он входит в паспортные данные
биполярного транзистора и обозначается
символом![]() .
.
В соответствии с новыми обозначениями формулы запишутся в виде:
![]()
![]()
![]() имеет
смысл входного сопротивления база-эмиттер
(при коротком замыкании выходной цепи),
имеет
смысл входного сопротивления база-эмиттер
(при коротком замыкании выходной цепи),
![]() - коэффициент обратной связи по напряжению
(при разомкнутой входной цепи) и
- коэффициент обратной связи по напряжению
(при разомкнутой входной цепи) и
![]() - выходная проводимость транзистора
(при разомкнутой входной цепи).
- выходная проводимость транзистора
(при разомкнутой входной цепи).
В новых обозначениях:
![]()
где
![]() -
напряжение, развиваемое на сопротивлении
-
напряжение, развиваемое на сопротивлении
![]()
На рис. приведена полная схема усилительного каскада, собранного по схеме с ОЭ. Выделим из этой схемы только те элементы, которые определяют её функциональное назначение.
Для этого придется отбросить емкость
![]() как принадлежащую выходной цепи
предыдущего каскада, цепь
как принадлежащую выходной цепи
предыдущего каскада, цепь
![]() назначение которой состоит в задании
начального положения рабочей точки на
ВАХ транзистора и цепь
назначение которой состоит в задании
начального положения рабочей точки на
ВАХ транзистора и цепь
![]() ,
служащую для температурной стабилизации
начального положения рабочей точки.
Таким образом, приходим к следующей
схеме, все элементы которой принципиально
необходимы для функционирования
устройства в качестве усилителя.
Используя матричный метод для активного
линейного четырехполюсника, проанализируем
свойства этой схемы.
,
служащую для температурной стабилизации
начального положения рабочей точки.
Таким образом, приходим к следующей
схеме, все элементы которой принципиально
необходимы для функционирования
устройства в качестве усилителя.
Используя матричный метод для активного
линейного четырехполюсника, проанализируем
свойства этой схемы.
Для анализа свойств усилителя как активного четырехполюсника составим эквивалентные схемы его входной и выходной цепей (см. рис).
Выходная часть эквивалентной схемы
эквивалентна реальной схеме только при
работе на переменном токе, когда из - за
наличия большой емкости блока питания
переменные потенциалы точек 1 и 2 можно
считать одинаковыми. По сравнению с
эквивалентной схемой обобщенного
активного четырехполюсника в
рассматриваемой схеме изменилось
определение нагрузочного сопротивления
четырехполюсника. Введем здесь
сопротивление
![]() ,
эквивалентное сопротивлению
,
эквивалентное сопротивлению
![]() в той схеме. Оно будет равно:
в той схеме. Оно будет равно:
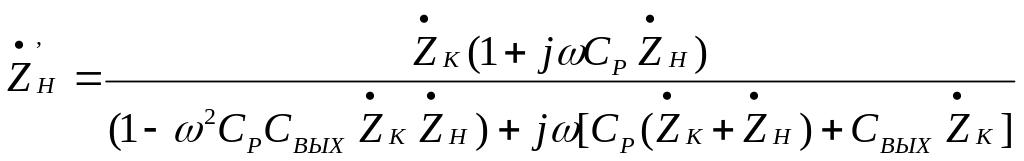 (24)
(24)
При таком представлении обе схемы
одинаковы и для оценки свойств усилителя
можно воспользоваться формулами (22) при
условии, что проводимость
![]() ,
т.е. что свойства четырехполюсника, в
основном, определяются свойствами его
нагрузки, а свойства активного элемента
описываются его h-параметрами.
,
т.е. что свойства четырехполюсника, в
основном, определяются свойствами его
нагрузки, а свойства активного элемента
описываются его h-параметрами.
Дальнейший анализ предполагает
конкретизацию нагрузки
![]() .
Прежде чем приступить к этому оценим,
как связаны h-параметры активного
четырехполюсника с ВАХ биполярного
транзистора, включенного по схеме с ОЭ.
.
Прежде чем приступить к этому оценим,
как связаны h-параметры активного
четырехполюсника с ВАХ биполярного
транзистора, включенного по схеме с ОЭ.
На рисунке приведены входные, выходные и проходные ВАХ биполярного транзистора.
На этих характеристиках ток
![]() и напряжение
и напряжение
![]() тождественны току
тождественны току
![]() и напряжению
и напряжению
![]() активного четырехполюсника, а
активного четырехполюсника, а
![]() и
и
![]() соответственно его параметрам
соответственно его параметрам
![]() и
и
![]() .
На основании формул (23) h-параметры
активного четырехполюсника и ВАХ
транзистора в схеме с ОЭ будут связаны
следующими соотношениями :
.
На основании формул (23) h-параметры
активного четырехполюсника и ВАХ
транзистора в схеме с ОЭ будут связаны
следующими соотношениями :
![]() (25)
(25)
Идентичность определения формул (25),
(23) и (3) позволяет утверждать, что для
описания параметров линейного усилителя
возможно применение матричного метода.
Иногда входную и проходную характеристики
транзисторов объединяют в одну :
зависимость
![]() ,
см.рис., и вводят параметр
,
см.рис., и вводят параметр
![]() ,
называемый крутизной. В этом случае
источник тока
,
называемый крутизной. В этом случае
источник тока
![]() в выходной цепи экв.схемы четырехполюсника
заменяется эквивалентным по величине
источником тока
в выходной цепи экв.схемы четырехполюсника
заменяется эквивалентным по величине
источником тока
![]() .
Действительно, так как
.
Действительно, так как
![]() ,
эти источники эквивалентны друг другу.
,
эти источники эквивалентны друг другу.
Частотные свойства апериодического усилителя
Из возможных классификационных свойств
усилителей выделяют два основных : по
виду связи между каскадами и по виду
коллекторной нагрузки
![]() .
Используя разработанную модель активного
четырехполюсника рассмотрим свойства
апериодического (
.
Используя разработанную модель активного
четырехполюсника рассмотрим свойства
апериодического (![]() )
и резонансного (
)
и резонансного (![]() )
усилителей с резистивнно-емкостной
связью между каскадами.
)
усилителей с резистивнно-емкостной
связью между каскадами.
Апериодический усилитель.
Эквивалентная схема выходной цепи
такого усилителя имеет вид (см. рис.).
Влияние входной цепи, в первом приближении,
учтено источником тока
![]() .
Частотные свойства будем анализировать,
используя понятие
.
Частотные свойства будем анализировать,
используя понятие
![]() .
.
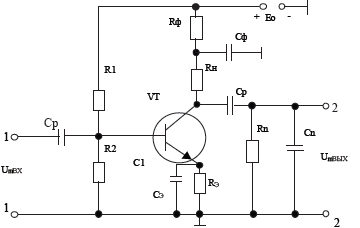
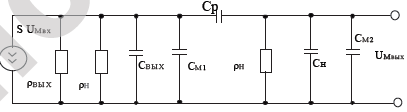
Для получения зависимости
![]() выразим
выразим
![]() через
через
![]() .
Для этого определим сначала напряжение
U1, на зажимах 1 - 1, создаваемое
током
.
Оно равно падению напряжения на
сопротивление, эквивалентом параллельно
- последовательной цепи, расположенной
справа от режимов 1 - 1. Обозначим это
сопротивление
.
Для этого определим сначала напряжение
U1, на зажимах 1 - 1, создаваемое
током
.
Оно равно падению напряжения на
сопротивление, эквивалентом параллельно
- последовательной цепи, расположенной
справа от режимов 1 - 1. Обозначим это
сопротивление
![]() и вычислим его:
и вычислим его:
![]() (27)
(27)
Тогда
![]() (28)
(28)
Напряжение на выходе усилителя, на зажимах 2 - 2 будет равно
![]() (29)
(29)
где
![]() - постоянная времени нагрузочной
цепи. На основании соотношений (26)
(29) находим частотный коэффициент
передачи
- постоянная времени нагрузочной
цепи. На основании соотношений (26)
(29) находим частотный коэффициент
передачи
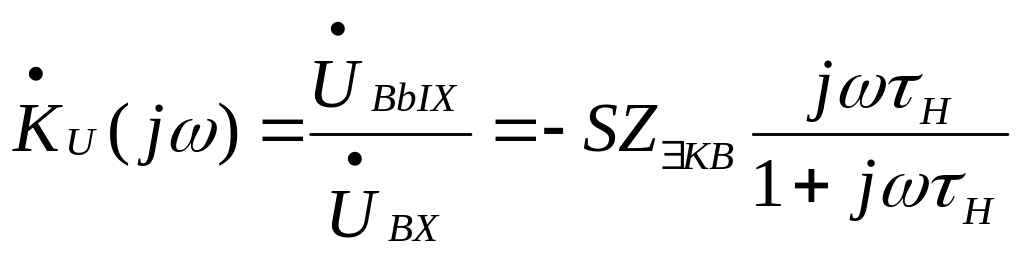 (30)
(30)
Проанализируем соотношение (30). Анализ удобно разделить на независимый анализ в области нижних, средних и верхних частот.
В области нижних частот (![]() )
сопротивление разделительного
конденсатора
)
сопротивление разделительного
конденсатора
![]() больше, чем сопротивление
больше, чем сопротивление
![]() ,
следовательно,
,
следовательно,
![]() .
Влиянием проводимости
.
Влиянием проводимости
![]() и
и
![]() в (30) можно пренебречь. Поэтому модуль
выражения (30) принимает вид (при
в (30) можно пренебречь. Поэтому модуль
выражения (30) принимает вид (при
![]() ).
).
![]() (31)
(31)
В области средних частот, где
![]() ,
следовательно,
,
следовательно,
![]() ;
проводимость
по-прежнему мала. Формула (30) еще больше
упрощается:
;
проводимость
по-прежнему мала. Формула (30) еще больше
упрощается:
![]() (32)
(32)
В области высоких частот проводимость
соизмерима с
![]() ,
и (30) принимает вид :
,
и (30) принимает вид :
![]() (33)
(33)
где
![]() .
На очень высоких частотах, соответствующих
условно
.
На очень высоких частотах, соответствующих
условно
![]() (33) упрощается :
(33) упрощается :
![]() (34)
(34)
Ниже построена АЧХ апериодического усилителя.
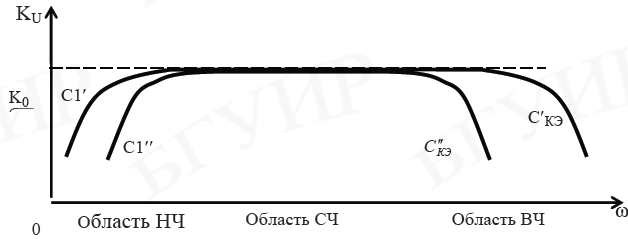
Изменение формы амплитудно-частотной
характеристики апериодического
транзисторного усилителя в зависимости
от величин разделительной
и паразитной
![]() емкостей.
емкостей.
Полоса частот, внутри которой
![]() ,
называется полосой пропускания усилителя.
Как следует из формулы (31) и (34) она равна
,
называется полосой пропускания усилителя.
Как следует из формулы (31) и (34) она равна
![]() (35)
(35)
Частотные свойства резонансного усилителя
Резонансный усилитель (линейный режим).
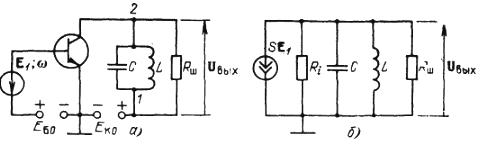
Резонансный усилитель (а) и схема замещения коллекторной цепи (б)
От резистивного усилителя отличается только видом нагрузочной цепи.
В данном случае нагрузкой является параллельный колебательный контур и шунтирующее его сопротивление нагрузки каскада ( ).
Для упрощения задачи будем считать, что
шунтирующее действие
велико и, поэтому, собственными потерями
в контуре можно пренебречь. Кроме этого,
можно пренебречь влиянием
![]() ,
поскольку резонансные усилители
работают, как правило, на высоких частотах
и поэтому 1/C<<RH.
,
поскольку резонансные усилители
работают, как правило, на высоких частотах
и поэтому 1/C<<RH.
С учетом принятых упрощений, полная
проводимость нагрузки источника тока
![]() будет равна
будет равна
![]()
Ранее принято, что
![]() ,
поэтому пренебрежем и влиянием
:
,
поэтому пренебрежем и влиянием
:
![]()
Учитывая, что
![]() и
и
![]() ,
последнее соотношение принимает вид :
,
последнее соотношение принимает вид :
![]()
где
![]() - обобщенная расстройка,
- обобщенная расстройка,
![]() -
добротность контура.
-
добротность контура.
Таким образом, полная проводимость
нагрузки источника тока
будет равна:
![]() (36)
(36)
Запишем выражение для комплексного коэффициента передачи, учтя, что ранее было пренебрежено влиянием емкости :
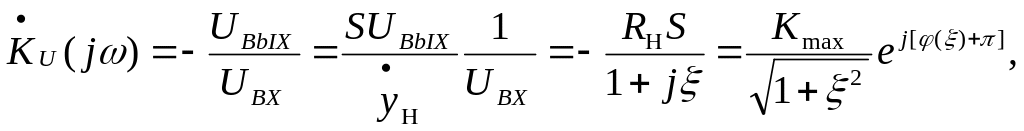 (37)
(37)
где
![]() - максимальное значение модуля
частотного коэффициента передачи на
резонансной частоте контура (
- максимальное значение модуля
частотного коэффициента передачи на
резонансной частоте контура (![]() );
);
![]() - фазочастотная характеристика контура.
- фазочастотная характеристика контура.
В формуле (37) соотношение
![]() определяет
комплексное сопротивление контура с
учетом внешних потерь в виде
.
Оно же определяет частотные свойства
коэффициента передачи
определяет
комплексное сопротивление контура с
учетом внешних потерь в виде
.
Оно же определяет частотные свойства
коэффициента передачи
![]() .
Таким образом, АЧХ резонансного усилителя
совпадает с АЧХ контура, образующего
нагрузочную цепь.
.
Таким образом, АЧХ резонансного усилителя
совпадает с АЧХ контура, образующего
нагрузочную цепь.
Отметим еще две особенности: 1. выходная емкость транзистора компенсируется (учитывается) при настройке контура в резонансе ;
2. на сопротивлении нагрузки не расходуется мощность источника питания, поэтому оно может быть выбрано очень большим, что обеспечивает высокое усиление на частотах, близких к резонансной.
Сущности и типы обратных связей в четырёхполюсниках
Одной из характерных черт любого электронного устройства является наличие или отсутствие обратной связи, т.е. связи, определяющей передачу на его вход части сигнала с его же выхода. Наличие такой связи может быть обусловлено следующими факторами:
1. физическими свойствами и конструктивными особенностями применяемых активных элементов. Это, так называемая, внутренняя обратная связь. (см. параметр h12) ;
2. неудачным расположением и монтажом различных элементов схемы, когда паразитные емкостные и индуктивные связи создают путь для передачи сигнала с выхода на вход. Это, так называемые паразитные обратные связи ;
3. специальными цепями, когда путь для передачи сигнала с выхода на вход устройства создается умышленно, для придания устройству нужных свойств. Это, так называемая, внешняя обратная связь.
Четырехполюсник, охваченный обратной
связью, можно представить в виде основного
четырехполюсника (без обратной связи)
с коэффициентом передачи
![]() и четырехполюсника обратной связи с
коэффициентом передачи
и четырехполюсника обратной связи с
коэффициентом передачи
![]() .
При этом вход последнего присоединен
к выходу, а выход - ко входу основного
четырехполюсника.
.
При этом вход последнего присоединен
к выходу, а выход - ко входу основного
четырехполюсника.
При сложении сигналов от источника
с колебаниями, поступающими через цепь
обратной связи, образуется результирующий
сигнал на входе основного четырехполюсника.
Он больше по величине чем
![]() ,
если оба этих сигнала складываются в
фазе, и меньше, если в противофазе. В
первом случае имеет место положительная
обратная связь, во втором - отрицательная
обратная связь.
,
если оба этих сигнала складываются в
фазе, и меньше, если в противофазе. В
первом случае имеет место положительная
обратная связь, во втором - отрицательная
обратная связь.
Практическое совпадение или противоположность фаз возможны только в ограниченном диапазоне частот, т.к. фазовый сдвиг из-за наличия реактивностей зависит от частоты. Из этого следует, что обратная связь, отрицательная на одних частотах, может быть положительной на других при одном и том же четырехполюснике обратной связи.
Оба четырехполюсника (![]() и
и
![]() )
составляют кольцевую цепь, которую
называют петлей обратной связи. Внутри
этой петли различают четыре способа
соединения этих четырехполюсников.
)
составляют кольцевую цепь, которую
называют петлей обратной связи. Внутри
этой петли различают четыре способа
соединения этих четырехполюсников.
