1. Телеграфный сигнал

Телеграфный сигнал - последовательность отрицательных и положительных импульсов с амплитудой и случайными длительностями .

Если плотности распределения и определяются показательными функциями.

(1)

(2)

Если - параметры распределения, то телеграфный сигнал можно считать стационарным процессом с корреляционной функцией

(3), где , - дисперсия, - амплитуда импульсов.

Телеграфный сигнал можно считать стационарным процессом с корреляционной функцией.

Параметр определяет спектральные и корреляционные характеристики процессов. При , получаем постоянную составляющую или детерминированный процесс.

Если , то телеграфный сигнал рассматривается как белый шум, наиболее существенная помеха в каналах связи и вычислительной технике. Определим интервал корреляции телеграфного сигнала:

(4)

Таким образом, интервал корреляции обратно пропорционален параметру .

- детерминированный процесс

- все сечения момента времени будут некорелированны.

Вычислим спектральную плотность телеграфного сигнала. Связь между спектральной функцией и корреляционной функцией определяется прямым преобразованием Хинчина-Винера.

Применяя 2 раза метод интегрирования по частям, получаем:

(5)

Ширина спектра

(6)

Из равенства следует, что чем уже полоса шумов, тем больше интервал корреляции, и наоборот.

2. Белый шум

Представляет собой наиболее существенную помеху. Белый шум - это сигнал с постоянной спектральной плотностью.

Белый шум можно получить их телеграфного сигнала, когда .

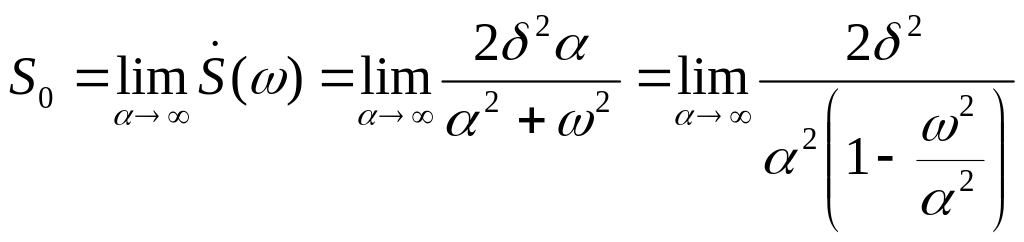
Для того, чтобы спектральная область , необходимо , следовательно дисперсия белого шума будет бесконечно большой величиной:

Дисперсия (7)

(8)

как квадрат амплитуды определяет мощность белого шума, поэтому равенство (8) определяет физический смысл .

Спектральная плотность белого шума численно равна мощности приходится на единичный интервал частот.

Определим корреляционную функцию белого шума.

(9)

Проанализируем выражение для корреляционной функции.

Рассмотрим 2 случая:

а)

б)

Учитывая данные пределы, получаем выражения.

(10)

Зная корреляционные функции мы можем определить спектральную функции белого шума:

Дельта-функция обладает фильтрующим свойством:

Используя данное фильтрующее свойство получаем,

Учитывая приведенные преобразования, можно сделать следующий вывод: белый шум представляет собой модель наиболее существенной помехи в каналах связи и вычислительной техники. К таким помехам относятся флунктуационные шумы и помехи многоканальных системах связи.

Белый шум обладает следующими свойствами:

1. Его спектральная плотность - постоянная величина. не зависящая от частоты.

2. Составляющие белого шума при модуле некоррелированы.

3. Дисперсия (мощность) белого шума неограниченны. Белый шум представляет собой идеализированное понятие. Не существует таких источников сигнала или помехи, которые давали бы бесконечно большую мощность и некоррелированные значения ближайших частот. Однако, этой идеализацией можно пользоваться, если действие помехи шириной спектра рассматривает в полосе частот полезного сигнала и соблюдается условие , где - полезный сигнал, - шум.