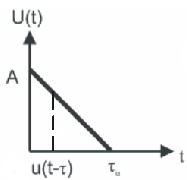
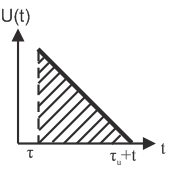
3. Автокорреляционная функция треугольного импульса

Рассмотрим треугольный импульс.

При

При

(4)

Автокорреляционная функция пачки из четырёх одинаковых прямоугольных импульсов, сдвинутых друг относительно друга на время T₁.

Ниже показан сигнал в виде пачки из четырех одинаковых импульсов, сдвинутых один относительно другого на время и соответствующая этому сигналу корреляционная функция. Вблизи зна­чений , равных , эта функция имеет такой же вид, как и для одиночного импульса. Максимальное значение кор­реляционной функции (при ) равно учетверенной энергии одного им­пульса.

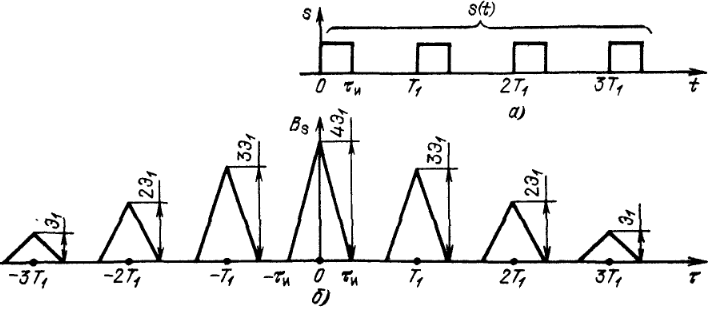
Пачка из четырех прямоугольных импульсов (а) и корреляционная функ­ция (б)

Для периодического сигнала, исходят из следующего определения:

При таком определении корреляционная функция приобретает размер­ность мощности, причем равна средней мощности периодического сигнала. Ввиду периодичности сигнала усреднение произведения или по бесконечно большому отрезку должно совпадать с усреднением по периоду . Поэтому выражение можно заменить выражением:

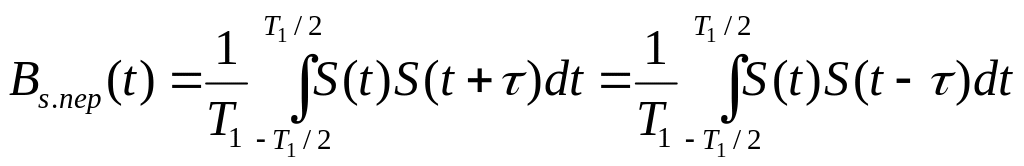
Входящие в это выражение интегралы суть не что иное, как корреля­ционная функция сигнала на интервале . Обозначая ее через , приходим к соотношению:

Очевидно также, что периодическому сигналу соответствует и пе­риодическая корреляционная функция . Период функции совпадает с периодом исходного сигнала . Например, для простейшего (гармонического) колебания корреляционная функция:

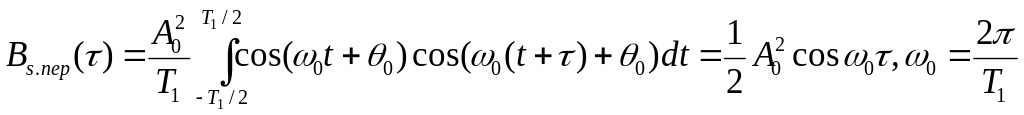
При , есть средняя мощность гармонического колебания с амплитудой . Важно отметить, что корреляционная функция не зависит от начальной фазы колебания .

Автокорреляционная функция периодического сигнала.

Для периодических функций энергия бесконечна, поэтому автокорреляционная функция определяется путем усреднения по периоду:

- средняя мощность сигнала.

В более общем случае не обязательно периодического, но с бесконечной полной энергией сигнала принимают:

Таким образом у такой автокорреляционной функции будет спектральная плотность мощности , что видно из соотношения:

Формально .

Однако практически спектральная плотность мощности определяется через функцию автокорреляции .

Понятие взаимной автокорреляционной функции.

Взаимная корреляционная функция характеризует степень связи между двумя разными сигналами.

Для вещественных функций и

Свойства взаимной корреляционной функции (ВКФ):

1) Они не является ни чётной ни нечётной функцией, т.е. .

2) Они остаётся неизменной при перемене чередования функций и изменений знака аргумента, .

3) Если случайные функции и не содержат постоянных составляющих и создаются независимыми источниками, то для них . Такие функции называются некоррелированными.

Соотношения между корреляционной функцией и спектральной характеристикой сигнала

Воспользуемся выражением , в котором положим , и соответственно . Тог­да получим:

Учитывая, что и , приходим к искомому соотно­шению

На основании известных свойств преобразований Фурье можно также написать.

Итак, прямое преобразование Фурье корреляционной функции дает спектральную плотность энергии, а преобразование дает корреляционную функцию .

Чем шире спектр сигнала, тем меньше интервал кор­реляции, т. е. сдвиг , в пределах которого корреляционная функция отлич­на от нуля. Соответственно чем больше интервал корреляции заданного сигнала, тем уже его спектр. Корреляционная функ­ция не зависит от ФЧХ спектра сигнала. Так как при заданном ам­плитудном спектре форма функции существенно зависит от ФЧХ, то можно сделать следующее заключение: различным по форме сигналам , обладающим одинаковыми амплитудными спектрами, соответствуют одинаковые корреляционные функции .

Случайные сигналы

Сигнал называется случайным, если его возникновение нельзя предсказать заранее или предсказать с вероятностью меньше единицы. Такого типа сигналы рассматривают на основе теории вероятности и математической статистики. Достаточно подробно случайные величины изучаются в курсе статистической радиотехники.

Мы рассмотрим основные элементы статистической физики. Величину называют случайной, если ее появление заранее неизвестно. Появление такой величины определяют при помощи параметра, называемого вероятностью и обозначают как .

Определим вероятность события на примере молекул газа, находящегося в замкнутом сосуде.

Пусть в сосуде молекул и из этих молекул обладают энергией . Вероятность того, что -молекул обладает энергией определим как отношение к общему числу молекул. Определенная таким образом величина называется вероятностью того, что молекул обладают энергией . Просуммировав данное равенство по всем молекулам:

, т.е. сумма всех вероятностей равна единице

Если событие с вероятностью равной единице, событие достоверно.

Умножим (5) на :

(6) - среднее значение.

Такое определение вероятности выполняется только для дискретных случайных величин.

Рассмотрим интервал значений , выберем в интервале длину .

Тогда, вероятность того, что случайная величина попадет в данный интервал зависит от ширины интервала и от того, в какой части числовой оси находится данный интервал.

Функция называется плотностью распределения, функция одномерна. Существует и двумерная трехмерная и -мерная функция распределения.

С физической точки зрения, плотность распределения численно равна вероятности попадания случайной величины в единичный интервал . Также как и для дискретной случайной величины среднюю величину , обозначают .

Корреляционные функции случайных сигналов и помех. Преобразования Хинчина-Винера.

Корреляционная функция

Корреляция - вероятностная зависимость одной случайной величины от другой. Такая зависимость возникает когда одна величина зависит от другой, а также от каких-либо факторов. Корреляция также возникает между случайными величинами, свойства которых имеют общие свойства для обеих величин.

Степень корреляции определяют при помощи корреляционных таблиц используемых корреляционных функций.

Корреляционной функцией называют вероятностную зависимость между величинами и случайного процесса в момент времени .

Корреляционную функцию определяют в виде:

(7), где

- двумерная плотности вероятности, - математическое ожидание процесса

(7)

Уравнение (7) определяет операцию усреднения

Корреляционная функция случайного сигнала с физической точки зрения определяется как среднее значение по множеству значений и .

Функция - одномерная плотность распределения.

Процесс называется стационарным, если все его характеристики не зависят от времени , а зависят только от времени наблюдения.

Корреляционная функция для стационарного процесса имеет вид:

(8)

Статистическая радиотехника вводит нормированную корреляционную функцию.

- дисперсия, определяющая разброс корреляционной функции.

Нормированная корреляционная функция обладает свойствами:

1. Она четная

2.

3. , если и

Интегральной характеристикой времени корреляции служит величина :

(9)

Если 2 сечения, и отстоят друг от друга на величину , то эти величины будут неколлерированны.

Экспериментальная оценка характеристик случайного сигнала

В экспериментах значение характеристик получают усреднением процессов и характеристик по времени.

Тогда математическое ожидание процесса определится как:

Аналогичное выражение можно записать для корреляционной функции

Эргостичность процесса

Процессы называют эргостичными, если характеристики, усредненные по времени и по множеству совпадают между собой. Как правило, стационарные процессы всегда являются эргостичными процессами.

Эргостичность процессов обладает очень важным свойством.

Если процесс эргостичный, то нет необходимости наблюдать за большим числом процессов. Достаточно наблюдать только 1 процесс в течение длительного времени. Все вероятностные характеристики при этом (корреляционная функция, спектральная функция, дисперсия) будут совпадать с теми значениями, которые получены при наблюдении множества процессов).

Преобразование Хинчина-Винера

Соотношение между корреляционными и спектральными характеристиками определяются преобразованием Хинчина-Винера, которое обобщает прямое и обратное преобразование Фурье для случайных сигналов. Вместо значений преобразований Фурье используется корреляционная функция. Преобразование Фурье Хинчина-Винера:

(10)

Учитывая четность функции , получим:

- прямое преобразование Хинчина-Винера

(11)

В качестве интегральной характеристики спектральной функции выбирается ширина спектра:

(12),

где - максимальное значение спектральной функции.

Взаимно корреляционная функция

Между случайными процессами корреляционная связь определяется взаимной функцией корреляции.

, где - математическое ожидание

Модели случайных сигналов: телеграфный сигнал, белый шум и Гауссовский процесс

Модель случайных процессов