1. Классификация сигналов. Амплитудно-временные парам. детермин. сигналов. (2)

2. Основные понятия обобщённой спектральной теории сигналов. (6)

3. Определение коэффициентов обобщенного ряда. Равенство Парсеваля. (8)

4. Гармонические базисные функции в разложении Фурье. (10)

5. Экспоненциальные базисные функции в разложении Фурье. (11)

6. Безфильтровый и фильтровый методы. (14)

7. Разложение в ряд Фурье непериодических сигналов. (14)

8. Распределение энергии в спектре непериодического колебания. (16)

9. Исследование сигналов с помощью преобразования Лапласа. (16)

10. Ортогональные разложения Котельникова для непрер.сигналов с огран.спектром. (18)

11. Ортогональные разложения Котельникова для непрер.сигналов с полос.спектром. (20)

12. Понятие автокорреляционной функции (на примере импульса прямоуг. формы). (21)

13. Автокорреляционная функция треугольного импульса. (23)

14. Автокорреляционная функция пачки из 4 прям.импульсов, ... на время T₁. (23)

15. Автокорреляционная функция периодического сигнала. (24)

16. Понятие взаимной автокорреляционной функции. (25)

17. Соотношения между корреляционной функцией и спектральной характ-й сигнала. (25)

18. Корреляционные функции случайных сигналов и помех. Преобр.Хинчина-Винера. (27)

19. Модели случайных сигналов: телеграфный сигнал, белый шум, Гауссовский проц. (29)

20. Узкополосые процессы. Аналитические сигналы. (32)

21. Радиосигналы с амплитудной модуляцией. (44)

22. Спектры однотональных и сложных амплитудно-модулированных сигналов. (45)

23. Балансная и однополосная модуляция. (47)

24. Радиосигналы с угловой модуляцией (основные определения). (48)

25. Частотно-модулированные колебания. Фазомодулированные колебания. (49)

26. Спектр колебаний при гармонической угловой модуляции. (51)

27. Определение линейной цепи. Дельта функция - как пример проб.сигнала. Св-ва. (55)

28. Временной метод анализа передачи сигналов через лин.цепи.Импул.и спектр.х-ки. (56)

29. Спектральный метод анализа передачи сигналов через линейные цепи. (57)

30. Особенности анализа процесса прохождения радиосигналов через избират.цепи. (59)

31. Матричный метод анализа свойств пассивного четырёхполюсника. (62)

32. Эквивалентные схемы пассивных четырёхполюсников. (64)

33. Характеристики линейных активных четырёхполюсников в системе h - пар-в. (65)

34. Характеристики линейных активных четырёхполюсников в системе z - пар-в. (67)

35. Характеристики линейных активных четырёхполюсников в системе у - пар-в. (68)

36. Транзисторный усилитель как пример активного четырёхполюсника. (68)

37. Частотные свойства апериодического усилителя. (71)

38. Частотные свойства резонансного усилителя. (73)

39. Сущности и типы обратных связей в четырёхполюсниках. (74)

40. Передаточная функция четырёхполюсника с обратной связью. (76)

41. Стабильность коэффициента передачи замкнутой системы с обратной связью. (78)

Классификация сигналов. Амплитудно-временные параметры детерминированных сигналов.

Теория сигналов

Электрическими сигналами называются изменения во времени заряда, напряжения или тока

Классификация сигналов

Все сигналы можно условно отнести к 4 классам:

1.Сигналы, произвольные по величине и непрерывные во времени. К таким сигналам относятся аналоговые сигналы (без разрыва) и континуальные сигналы (с разрывами)

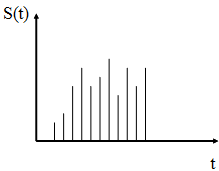
2. Сигналы, произвольные по величине и дискретные по времени. Сигналы такого рода называются дискретными сигналами.

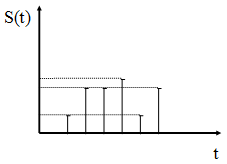
3. Сигналы, квантованные по уровню и непрерывные по времени. Такие сигналы называются квантованными.

4. Сигналы, квантованные по уровню и дискретные по времени. Такие сигналы называются цифровыми сигналами

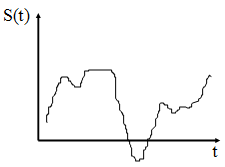
Все 4 типа сигнала называются детерминированными, если их мгновенное значение можно предсказать с вероятностью равной единице. Если мгновенное значение сигнала заранее неизвестно и его можно определить с вероятностью меньше единицы, то такие сигналы называются случайными.

К детерминированным относятся: несущее, управляющее колебание. К случайным: любой реальные сигнал и цифровые сигналы.

Все 4 класса могут быть детерминированными, так и случайными.

Детерминированные описываются амплитудными параметрами.

Случайные сигналы рассматривают на основе теории вероятностей и математической статистики.

Тем не менее детерминированные сигналы рассматриваются как начальное приближение случайных сигналов, поэтому изучение сигналов начинают с исследования основных характеристик детерминированного сигнала.

1. 2. 3. 4.

Амплитудно-временные параметры детерминированных сигналов

Рассмотрим зависимость виде идеального прямоугольного импульса и на его основе рассмотрим параметры реального сигнала.

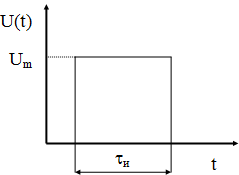
Реальные импульсы значительно отличаются от такого идеального прямоугольного импульса

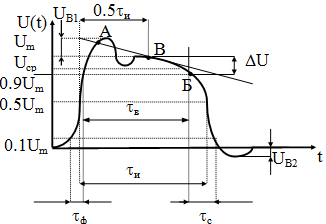
- амплитуда импульса, - вершина импульса, -скол вершины, - выброс среза, - длительность фронта, - длительность импульса, - длительность среза, - длительность вершины.

Для многих сигналов параметры могут добавляться или исключаться.

Периодическая последовательность прямоугольных импульсов с периодом и длительностью .

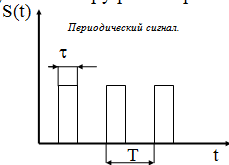
Энергия такой последовательности по отношению к максимальной энергии характеризуется скважностью , коэффициент заполнения:

Зная параметры импульса, строят их математические модели. Наиболее широко применяется метод кусочной аппроксимации.

При таком методе ось времени разбивается на интервалы , на которых задается аналитический вид сигнала. Иногда сигналы в таких интервалах можно представить в виде линейной функции.

- такой метод называется линейной аппроксимацией.

В качестве примера рассмотрим зависимость в виде трапеции.

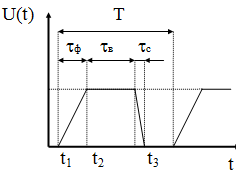
Построим математическую модель для сигнала, применяя метод кусочной аппроксимации. При

При

При

При

При

Динамическое представление

Все сигналы можно представить в виде суммы элементарных сигналов, если длительность таких сигналов стремится к нулю, то мы достаточно точно можем описать реальный сигнал. Такое представление называется динамическим представлением.

В качестве элементных сигналов выбирают функцию Хевисайда или дельта-функцию. Существует 2 способа динамического представления:

В первом способе элементарный сигнал представляется в виде ступеней, длительность ступеней одинакова, равна дельта, высота ступеньки равна разности мгновенных значений сигнала на концах интервала.

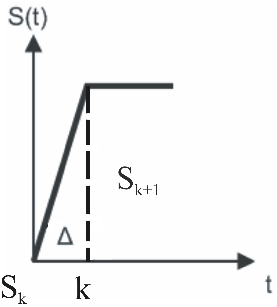
При втором способе сигнал представляется в виде суммы бесконечно маленьких прямоугольных импульсов.

Рассмотрим свойства таких элементарных импульсов

При

При

(1)- математическая модель сигнала

Данная функция описывает переход из нулевого состояния в единичное состояние.

Если , то такой переход будет мгновенным.

- функция Хевисайда - мгновенный переход из 0 в 1.

Из способа создания Хевисайда

Если импульс начинается с момента времени (момента ), то функция Хевисайда имеет вид: (2)

Построим математическую модель сигнала, используя первый способ динамического представления и функцию Хевисайда.

при можно представить в виде бесконечной малой величины

и сумму заменить интегралом:

(3)

При втором способе динамического представления используем прямоугольный импульс малой длительности.

Рассмотрим свойства такого импульса

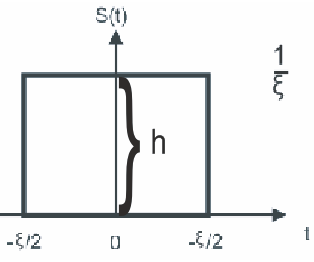
Площадь такого импульса

если

Математическая модель импульса

(4)

Если начало отсчета смещено на , то

Зная определение функции , определим второй способ динамического представления.

Выберем произвольный -й импульс:

Если , можно ввести непрерывную функцию и суммирование заменить на интегрирование

(5)

Формула (5) называется фильтрующим свойством дельта-функции

Основные понятия обобщённой спектральной теории сигналов

Спектральный анализ и синтез детерминированных сигналов

Метод кусочных аппроксимаций и другие аналитические методы не решают в полном объеме задачу обработки сигналов и построения их математических моделей. Частично такие задачи можно решить на основе обобщенной спектральной теории детерминированных сигналов.

Элементы обобщенной спектральной теории

Обобщенной спектральной теорией называется совокупность методов представления сигнала в виде суммы ортогональных базисных функций с весовыми множителями .

Данное разложение имеет следующий вид: (1)

Базисные функции обладают следующими свойствами:

1. Ряд сходится.

2. Базисные функции должны иметь простую математическую форму.

3. Коэффициенты должны определяться достаточно просто.

Разложение в форме (1) называется обобщенным рядом Фурье.

Система функций называется ортогональной, если выполняется условие ортогональности и нормировки:

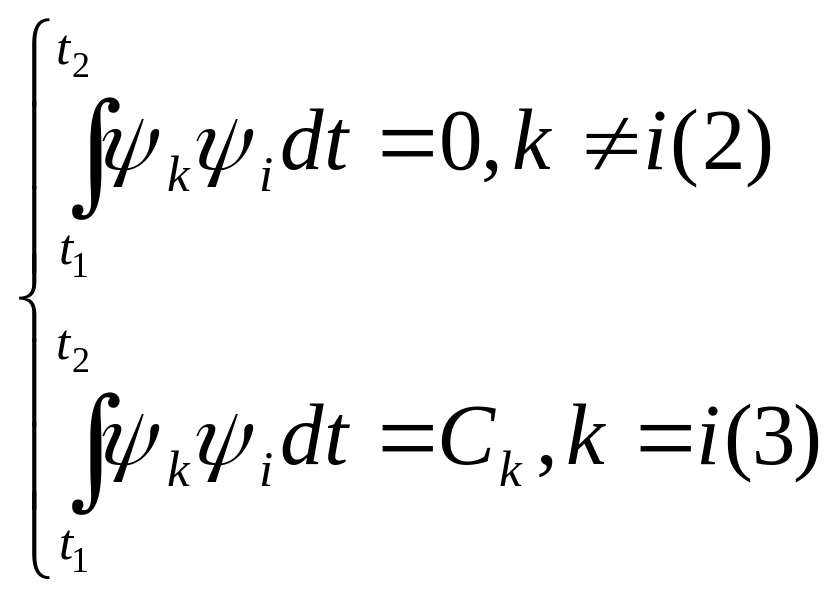
Коэффициент называется нормой для системы функций

Функция называется нормированной функцией

Система функций удовлетворяет условию ортогональности.

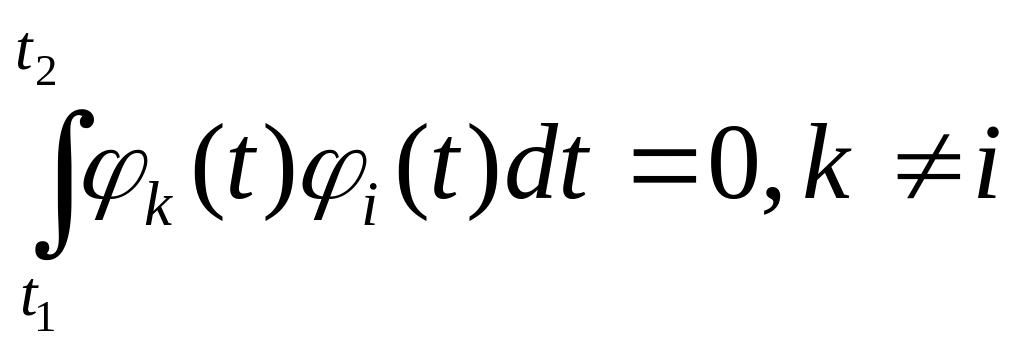
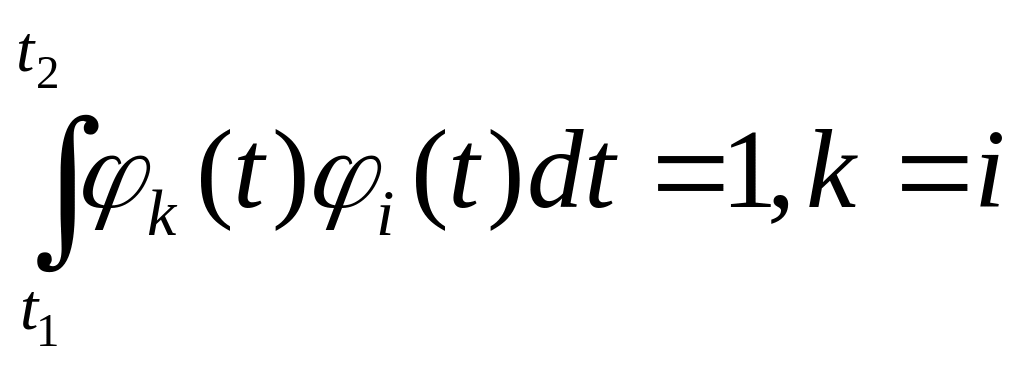
Функция, удовлетворяющая условиям нормировки и ортогональности называется ортогональной.

Для ортогональных базисных функций выполняется равенство Парсеваля.

Мощность суммы с ортонормированных сигналов равна алгебраической сумме мощностей каждого из составляющих сигнала:

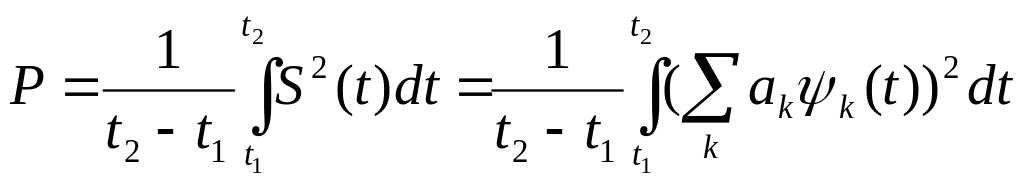
Используя условие ортогональности, мы получаем, что мощность равна:

(4)

Равенство (4) называется равенством Парсеваля, если под функцией или понимают ток или напряжение, то условие ортогональности с физической точки зрения можно трактовать следующим образом:

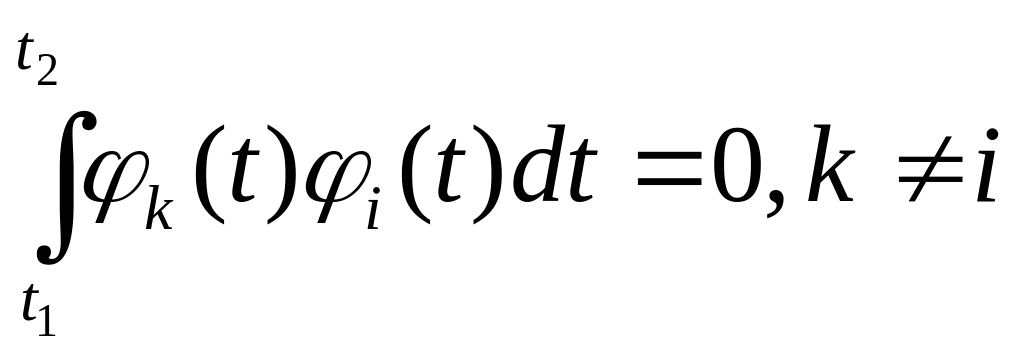, значит взаимная энергия сигнала равна нулю и следовательно, ортогональные сигналы не взаимодействуют между собой.

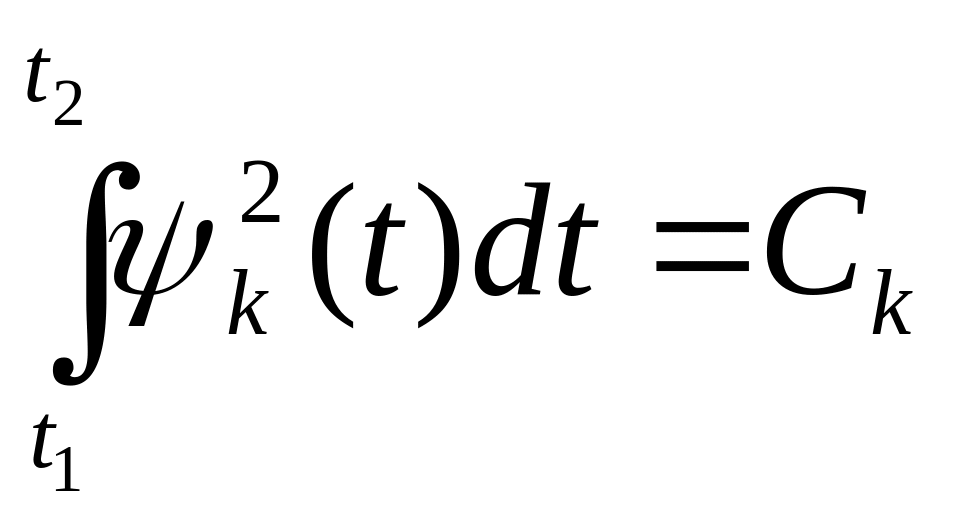
Из определения мощности следует, что условия нормировки можно трактовать как энергию, выделяемую на сопротивлении в 1 Ом.

Таким образом, обобщенная спектральная теория исследует общие закономерности спектрального анализа для системы базисных функций и изучает возможности выбора базисных функций для задач прохождения и обработки сигнала.

Определение коэффициентов обобщенного ряда. Равенство Парсеваля

Определение коэффициентов разложения

Рассмотрим обобщенный ряд Фурье:

разложим обе части равенства на и проинтегрируем:

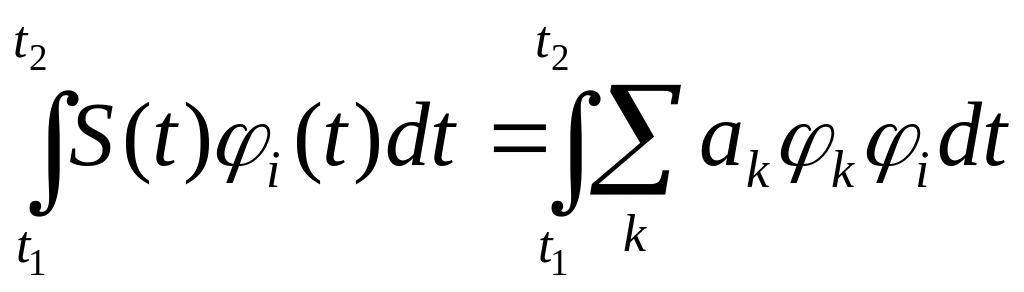
Для ортогональной системы функций операторы интеграла и суммы можно поменять местами

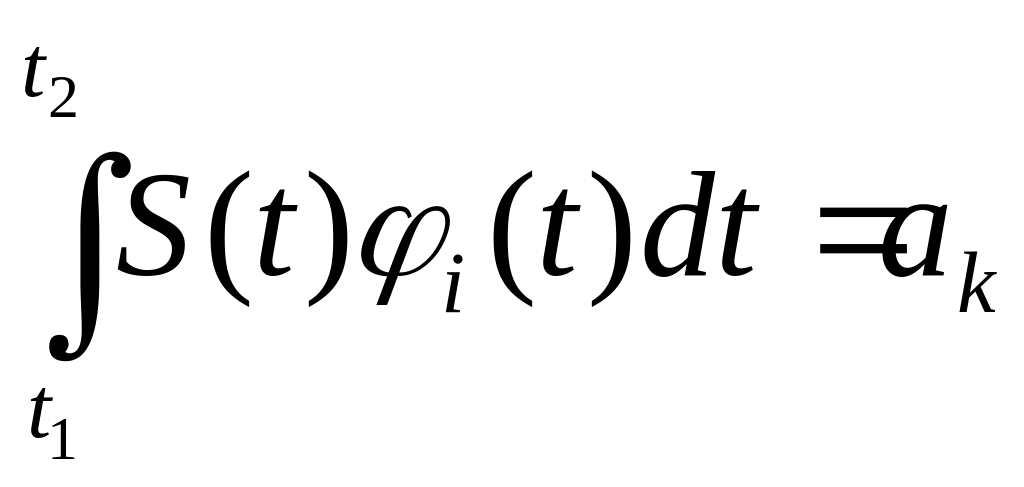
Минимизация погрешности разложения

Определим оптимальные коэффициенты в разложении , при которых разложение имеет минимальную погрешность. Определим погрешность как среднеквадратичную погрешность:

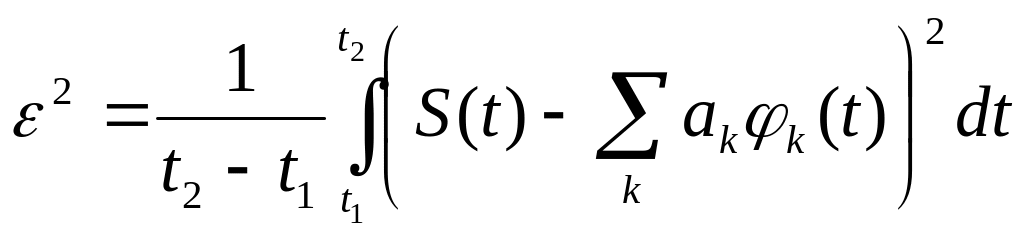
Используя условие ортогональности, получим:

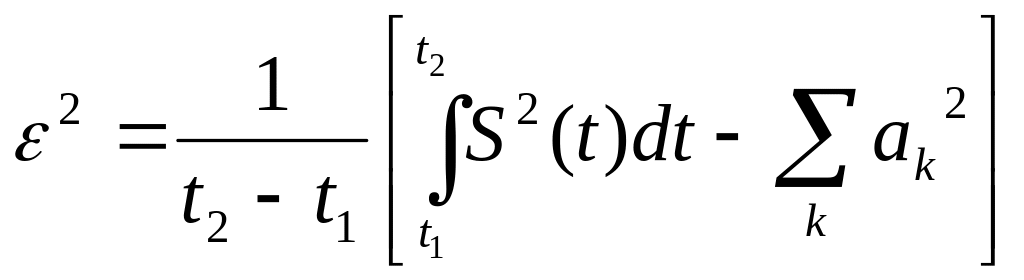
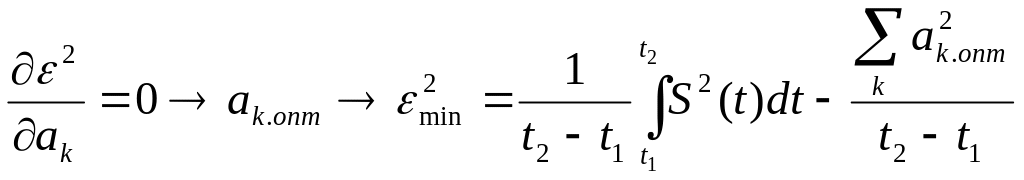(6)

Впервые такую задачу решил Фурье. Фурье показал, что , если

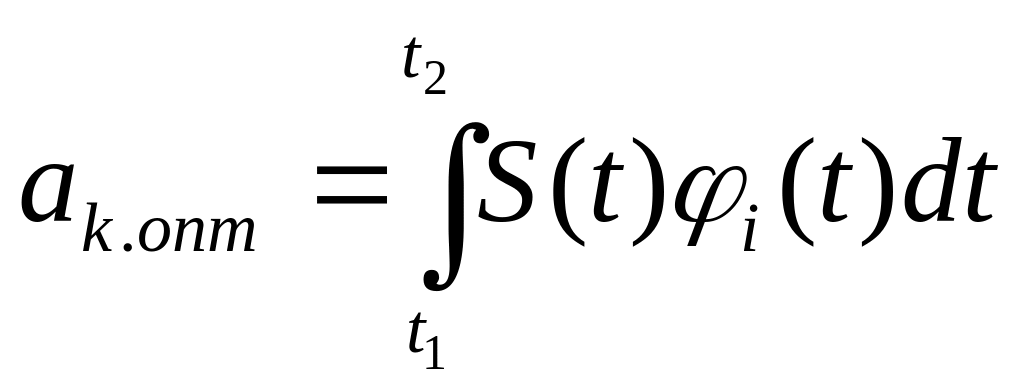при

Равенство (6) преобразуется в равенство Парсеваля.

Если , то и мы допускаем погрешность в разложении.

Выбор количества членов ряда

В радиотехнике используют сигналы, 80-90% энергии которых сосредоточено в слагаемых с номерами . 20-10% энергии будут составлять погрешность в разложении.

Погрешность будем называть относительной погрешностью

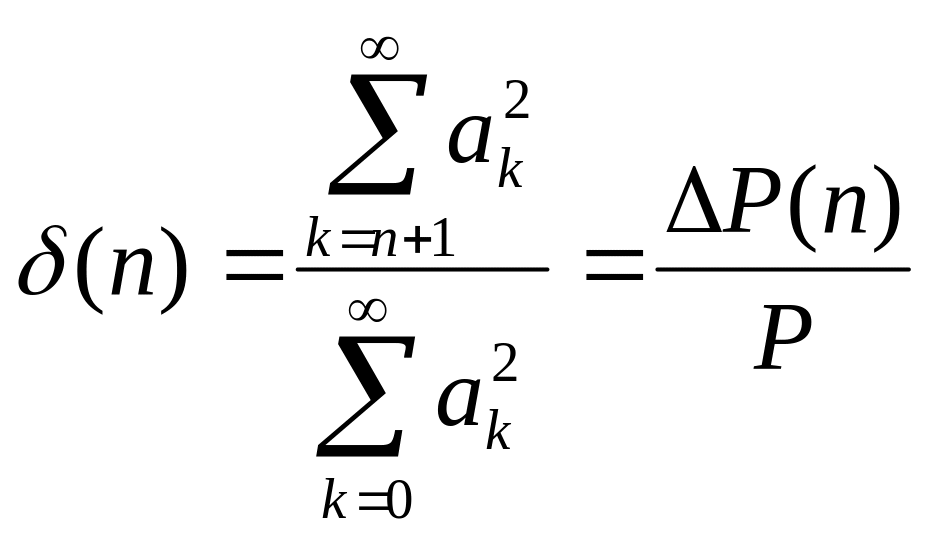
Задавая погрешность определяем количество членов ряда .

Ортогональные функции

В качестве ортогональных функций выбираются функции Бесселя, Хаара, Уолша. Кроме того, используют полиномы Лагерра, Лежандра, Эрмита, Чебышева.

Реальные сигналы всегда ограничены по времени и неограниченны по частотам, поэтому в радиотехнике искусственно рассматривают сигналы на полубесконечном либо бесконечном интервале времени .

Если сигнал ограничен по времени, его рассматривают на интервале .

Взаимная энергия и мощность детерминированных сигналов

Для определения связи между сигналами вводят понятия взаимной энергии и мощности. Взаимная энергия и мощность определяется как:

Если сигналы ортогональны (не взаимодействуют), то .

Сигналы, ортогональные по мощности образуют более широкий класс, в который входят сигналы, ортогональные по энергии, т.к. мощности сигналов привязаны к конечному интервалу времени. В то же время из ортогональности по энергии следует ортогональность по мощности.

Условие ортогональности и когерентности

Два сигнала и называются ортогональными по энергии или по мощности , если их взаимная энергия равна нулю .

(1)

(2)

Сигналы, ортогональные по мощности, образуют более широкий класс, в который входят сигналы, ортогональные по энергии. Это связано с тем фактором, что сигналы, ортогональные по мощности, привязаны к конечному интервалу времени, в то же время из ортогональности по энергии следует ортогональность по мощности, но не наоборот, т.к. понятие взаимной энергии более общее понятие.

Сигналы, для которых мощность называют когерентными сигналами.

Взаимная энергия и мощность характеризует степень сходства двух сигналов.

Если два сигнала идентичны , то они когерентные.

- когерентная мощность.

Для ортогональных сигналов , значит ортогональные системы будут полностью некогерентными.

Если , то такие сигналы называются частично когерентными сигналами.

На конечном интервале времени понятие взаимной энергии и мощности выполняется одновременно.

Ортогональность постоянных и переменных составляющих

Пусть сигнал содержит постоянную составляющую и переменную составляющую , где

Постоянные и переменные составляющие ортогональны между собой и их распространение через цепь можно считать независимым событием.

Среднее значение переменной составляющей будет равно нулю.

Гармонические базисные функции в разложении Фурье

Пример базисных функций

В качестве базисных функций в наиболее общем случае выбираются гармонические функции и - частота основной гармоники .

Покажем, что и ортогональны:

, если

Аналогично можем показать ортогональность , следовательно любой сигнал можно представить в виде:

(3)

умножим (3) на (2) и проинтегрируем, используя условие ортогональности и нормировки.

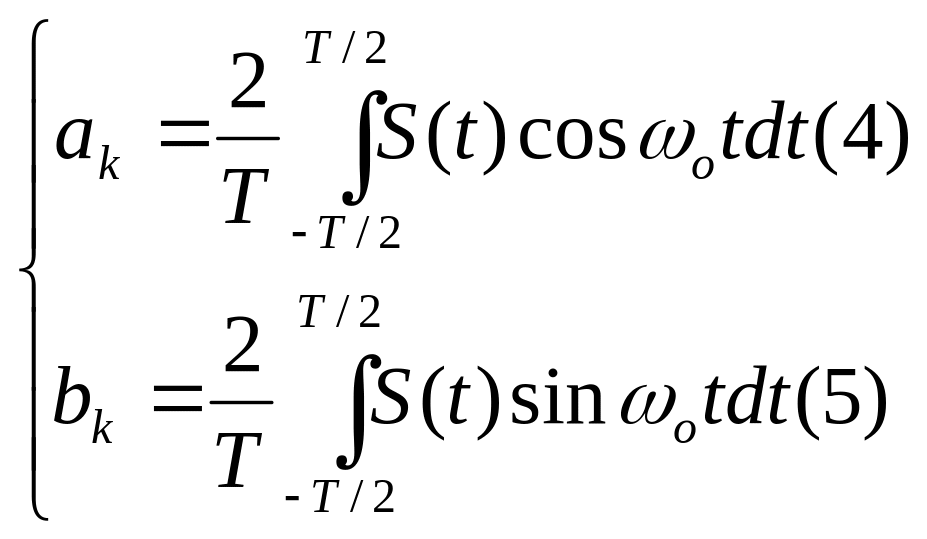
Выражению (3) можно придать другой вид:

Введем обозначения:

Возведем в квадрат и сложим их:

,

где - амплитуда гармонического сигнала, - фаза.

Таким образом, любой периодический сигнал полностью определяется суммой гармоник.

Экспоненциальные базисные функции в разложении Фурье.

2. Экспоненциальные функции

При преобразовании сигнала целесообразно использовать разложение по экспоненциальным функциям комплексного аргумента.

Синусы и косинусы - ортогональные функции. Используем формулы Эйлера для доказательства ортогональности экспоненциальных функций.

(6)

Сложим 2 выражения:

С учетом таких обозначений, получим:

(8)

Умножим обе части на и проинтегрируем

(9)

-модуль

- фаза

Из соотношений следует, что образует комплексный дискретный спектр частот, , соответственно модуль также будет являться дискретным спектром и называться амплитудно-частотной характеристикой; называется дискретной фазовой характеристикой или дискретной фазо-частотной характеристикой.

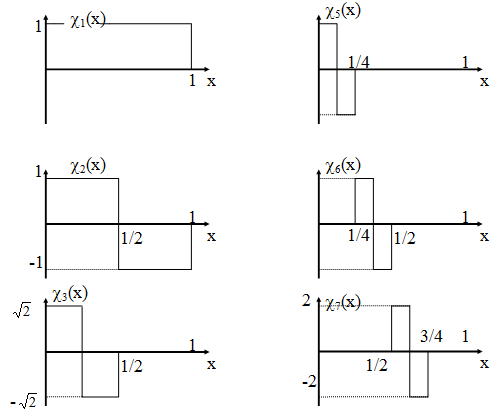
3. Функции Хаара

Для анализа и синтеза сигналов с импульсными характеристиками применяют функцию Хаара. Ортогональные функции Хаара , зависящие от , применяются для разложения в ряд на интервале значений от 0 до 1, .

Разложение:

(10) - условие нормировки

Функции Хаара достаточно просто генерируются в устройствах и представляют собой совокупность импульсов прямоугольной формы, поэтому их используют для анализа и синтеза импульсных процессов.

Определение функций Хаара тесно связано с понятием двоичного отрезка. Отрезки, полученные делением интервала на отрезка называется двоичными отрезками. Двоичные отрезки всегда замкнуты слева и замкнуты справа только в одном случае, когда справа стоит 1, во всех остальных случаях двоичные отрезки считаются разомкнутыми справа - разомкнут справа

Длину двоичного отрезка обозначают:

, где - число разбиений и - номер отрезка от 1 до , - число разбиений

Обозначим левую половину отрезка через , правую половину

Функции Хаара:

Чтобы применить функцию Хаара для импульсных сигналов, нужно заменить на безразмерную величину:

Полиномы Лагерра

При анализе сигналов сложной формы необходимо отбирать небольшое количество членов ряда, т.к. ряд должен быстро сходиться. Для анализа таких сигналов применяют полиномы Лагерра

Чтобы использовать полином, заменяют

Полином является решением уравнения (1)

Решение ищем в виде (2)

Подставляя степенной ряд в уравнение (1) и приравнивая коэффициенты при равных степенях , получаем, что:

Из свойств Лагерра следует,

С учетом данных соотношений, выражение для полинома Лагерра:

(3)

Полиномы Лагерра ортогональны с весовым множителем

Ортогональная система - функция Лагерра

Между полиномом Лагерра существует связь, которая называется реккурентным соотношением:

(4)

Полиномы применяются для анализа сигналов, которые определяются дельта-функцией или функцией Хевисайда.

Безфильтровый и фильтровый методы.

Экспериментальные методы спектрального анализа

Для экспериментального определения состава гармоники сигнала применяются 2 метода:

1. Безфильтровый

2. Фильтровый

1. В первом методе используется установка, структурная схема которой имеет вид:

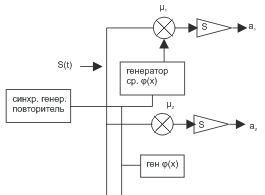
Сигнал , содержащий гармоники подается на множительные элементы . На эти же множительные элементы подаются функции .

На множительных элементах сигналы перемножаются и поступают в интегратор. К концу времени действие сигнала на выводах интегратора создаются постоянные составляющие сигнала, которые равны коэффициентам в разложении .

2. В фильтровом методе используется колебательный контур, настроенный на определенную резонансную частоту. Если частота гармоники совпадает с собственной частотой контура, то мы наблюдаем максимальный сигнал (резонанс) токов при параллельном контуре, напряжений - при последовательном контуре.

Разложение в ряд Фурье непериодических сигналов.

Спектральное представление непериодических сигналов

Любой периодический сигнал можно разложить в ряд Фурье. В непериодической системе период неизвестен и разложить функцию в ряд нельзя. Для разложения в ряд периодических функций применяют различные методы, наиболее широко используют метод, в котором непериодический сигнал представляется в виде периодического сигнала.

Преобразуем сигнал .

(5)

(6)

Периодическую функцию уже можно разложить в ряд Фурье:

(7)

В пределе при :

Это означает, что соседние дискретные частоты и спектр вместо дискретного становится непрерывным.

Такое представление дает возможность заменить сумму на интеграл

Функция (8) называется спектральной плотностью (спектральной функцией).

Значение спектральной функции зависит только от формы сигнала . Зная форму сигнала , можно определить спектральный состав сигнала.

Данное равенство называется прямым преобразованием Фурье.

(9) - обратное преобразование Фурье.

Из уравнения (8), (9) следует, что - пара Фурье.

Комплексные функции можно представить в виде:

Модуль спектральной функции называется амплитудно-частотной характеристикой

спектра и по форме совпадает с сигнала . Зависимость называется фазо-частотной характеристикой.

Распределение энергии в спектре непериодического колебания.

Мощность определяется как среднее значение энергии, выделяющейся за конечный интервал времени или за период .

Среднее значение зависит от колебаний. Для непрерывного сигнала , значит понятие мощности к обычным сигналам неприменимо.

В связи с этим вводят понятие спектральной плотности энергии.

Получим данный параметр на основе теоремы Парсеваля.

По теореме Парсеваля, если две функции и интегрируемые и , то произведение этих функций с их спектральными плотностями связаны между собой соотношениями:

,(10) где - функция, комплексно-сопряженная с функцией

Пусть сигналы идентичные:

(11)

называется спектральной плотностью энергии.

Спектральная плотность энергии численно равна энергии, приходящейся на частоту в 1 Гц.

Исследование сигналов с помощью преобразования Лапласа.

Применение преобразования Лапласа к анализу неинтегрируемых функций

Функцию можно разложить в ряд Фурье (периодическую или непериодическую), если функция интегрируема. Большинство функций не относится к этому классу:

Например функция Хевисайда

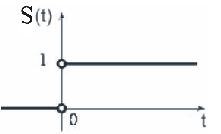
Дельта функция:

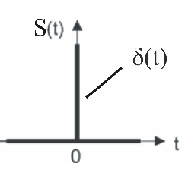
Для разложения в ряд неинтегрируемых функций применяют различные методы. Наиболее широко используют метод множителя сходимости. При таком методе функцию умножают на некоторую функцию, создающую множитель сходимости, а затем совершают предельный переход.

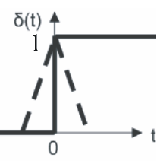
- множитель сходимости

В общем случае такой множитель ввести нельзя, поэтому данный метод расширяют, вводя понятия комплексной частоты.

, - множитель сходимости

Т.к. частота бывает комплексной, то все критические точки интеграла будут находиться внутри контура и при интегрировании по контуру не будут давать вклад в интеграл, значит .

Представим:

Рассмотрим функцию . Применим к обратное преобразование Фурье, предварительно введя множитель сходимости

(12)

(13)

- спектральная функция

Выражение (13) называется обратным преобразованием Лапласа. Аналогично можно ввести прямое преобразование Лапласа:

Аналогично можно получить спектральную плотность

Преобразование Лапласа широко используется и для анализа ступенчатых функций типа функции Хевисайда и дельта-функции.

Ортогональные разложения Котельникова для непрерывных сигналов с ограниченным спектром.

Ортогональное разложение Котельникова для непрерывных сигналов

С целью упрощения анализа непрерывных сигналов в инженерных расчетах учитывается только та часть спектра, в которой содержится 80-95% энергии. Такие сигналы можно считать ограниченными по спектру и применять к ним разложение Фурье. Наряду с разложением Фурье используется ортогональное разложение Котельникова, которое имеет преимущества по сравнению с разложением Фурье. Ортогональное разложение Котельникова дает возможность представить непрерывные сигналы в виде последовательности импульсов, отстоящих друг от друга на один и тот же интервал времени .

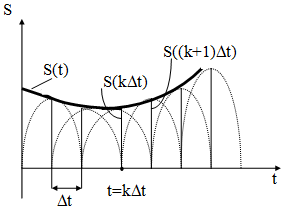
Теория ортогонального разложения Котельникова основана на теореме Котельникова: любой непрерывный сигнал, не содержащий частоты выше , может быть представлен в виде значений сигнала , расположенных друг от друга на один и тот же интервал времени .

Интервал называется интервалом дискретизации. Число необходимых отсчетов (1)

Число разбиений называется базой сигнала. Разложение Котельникова имеет вид:

(2), где значение называется отсчетами сигнала. Базисные функции называют функциями отсчета. При разложении сигнала с ограниченным спектром базисная функция (3)

Базисные функции обладают условием ортогональности

- норма функции ( ).

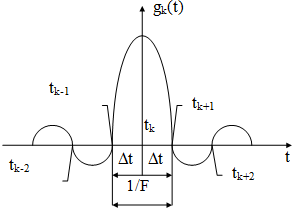
Интервал дискретизации в 2 раза меньше максимального периода , следовательно при разложении в ряд Котельникова можно учитывать число членов ряда в 2 раза меньше, чем в разложении Фурье при одной и той же погрешности. Погрешность 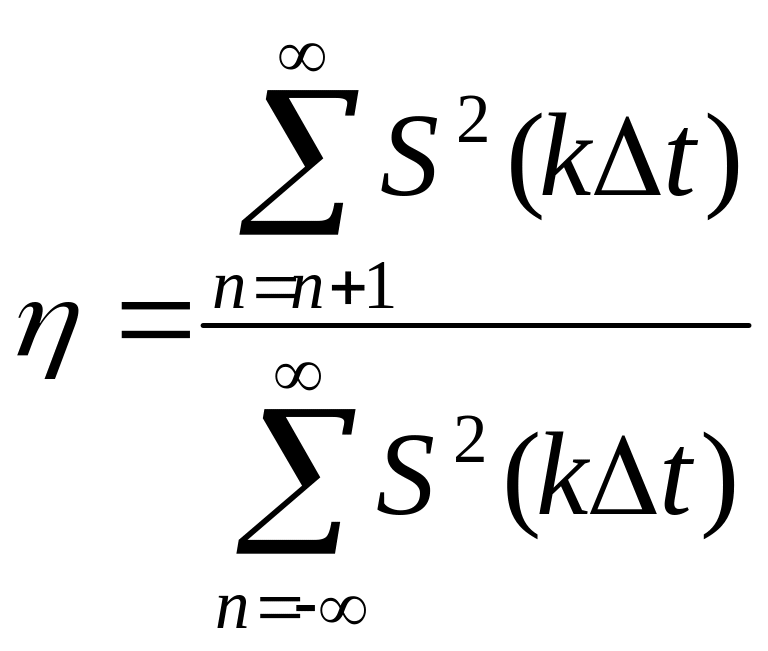(4)

Энергия сигнала равна аддитивной сумме энергий каждой составляющей сигнала.

Разложение Котельникова обладает рядом особенностей:

1) Базисные функции выбираются так, что ряд носит формальный характер, т.е. любое фиксированное значение и отсчет определяет полностью ряд, все остальные составляющие ряда равны нулю;

2) Отсчеты функции можно определить либо аналитически, либо экспериментальным путем и не требует дополнительных вычислений;

3) Простота анализа сигналов и процесса восстановления сигнала по импульсной последовательности, поэтому разложение Котельникова широко используют для передачи непрерывных сигналов в виде узких импульсов.

Рассмотрим подробно процесс восстановления сигналов низких частот с частотой среза очень узкой полосой, поэтому если взять любой отсчет и сформировать импульс амплитуды и длительности , то его можно легко передавать по эфиру. Таким образом, непрерывный сигнал представляет собой последовательность очень узких импульсов. На приемной станции находится приемник, который преобразует последовательность очень узких импульсов, расположенных друг от друга на интервале в непрерывный сигнал

Ортогональные разложения Котельникова для непрерывных сигналов с полосовым спектром.

Сигналы с полосовыми спектрами

Рассмотрим сигнал, в определенной полосе частот .

Интервал дискретизации

Введем среднюю частоту (5)

Такой сигнал можно разложить в ряд Котельникова, но разложение будет иметь другой вид:

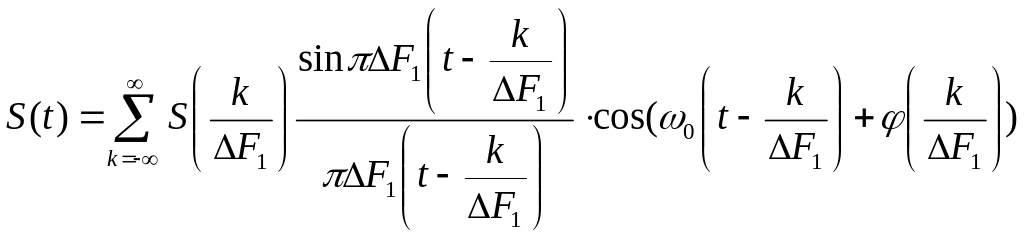(6)

Разложение Котельникова для сигналов с полосовыми спектрами обладает следующими особенностями:

1. Базисные функции представляют собой колебания, модулированные частотой .

2. Кроме отсчетов значений , надо учитывать и отсчеты фаз .

3. Число необходимых отсчетов .

Сигналы частотной области

В ряде случаев возникает необходимость разложения спектральной функции в ряд Котельникова.

Разложим спектральную функцию в ряд Котельникова, используя разложение для сигналов с ограниченным спектром и двойное преобразование Фурье.

Данные преобразования формально соответствуют друг другу, поэтому если в ортогональном разложении Фурье для функции с ограниченным спектром

, то разложение имеет следующий вид:

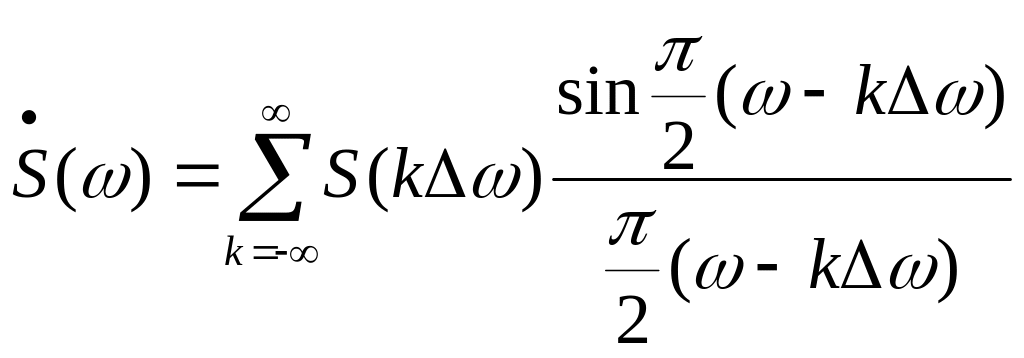(7)

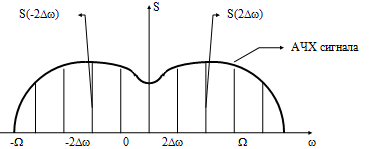
Спектральная функция - комплексная функция и следовательно содержит реальные и мнимые части, отсюда следует, что число слагаемых в (7) удваивается (надо записать для реальной и мнимой частей).

В действительности, т.к. , то число членов ряда остается неизменным. В целом, ортогональное разложение Котельникова является теоретической базой для передачи непрерывных сигналов в виде совокупности импульсов малой длительности.

Понятие автокорреляционной функции (на примере импульса прямоугольной формы).

Автокорреляционная функция

Автокорреляционная функция определяет связь между прямым сигналом и задержанным сигналом , -время задержки.

К такому понятию можно прийти, анализируя передачу сигнала в антенне на цель и приему отраженного от цели сигнала.

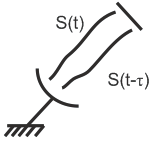
По времени задержки можно определить расстояние до цели.

С целью определения автокорреляционной функции рассмотрим скалярное произведение и

По аналогии со скалярной суммой векторов вводится скалярное произведение

Таким образом, скалярное произведение двух функций определяет взаимную энергию сигналов или степень их взаимодействия. Скалярное произведение обладает рядом особенностей:

1.

2.

3.

Автокорреляционная функция определяется как скалярное произведение прямого и задержанного сигнала:

(8)

Из вида функции следует, что она обладает свойствами:

Для скалярного произведения вводится функция Релея:

Автокорреляционная функция (8) вводится только для действительных функций, если функция мнимая, то , где -сопряженная функция.

Примеры вычисления автокорреляционной функции

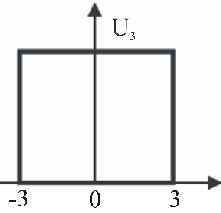
1. Автокорреляционная функция видеоимпульса. Рассмотрим видеоимпульс.

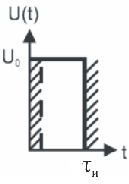
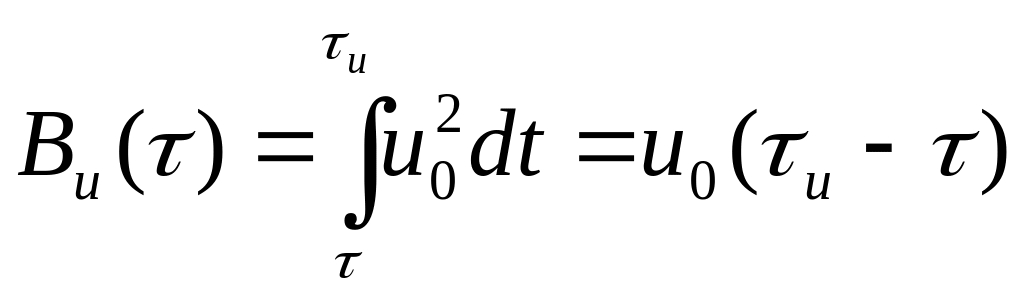
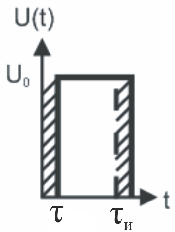
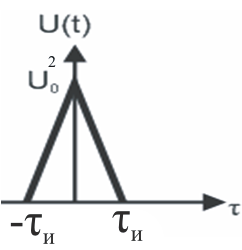
2. Автокорреляционная функция радиосигнала

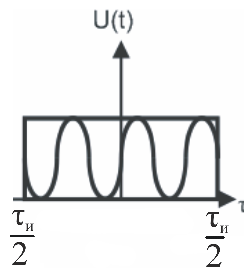
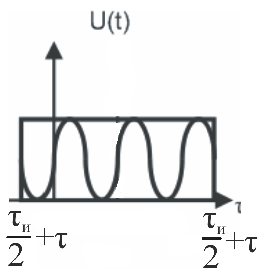
(1)

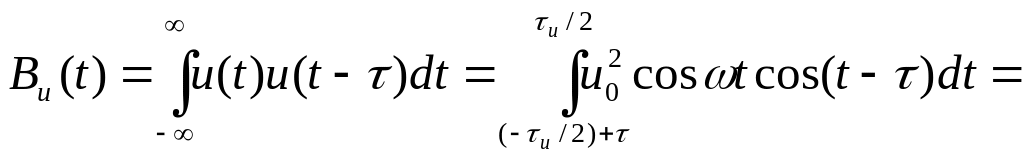
(2)

Автокорреляционная функция - гармоническая функция времени задержки , т.к. сдвиг может быть вправо и влево относительно оси , то в общем случае автокорреляционная функция:

(3)

Автокорреляционная функция треугольного импульса.