
- •2. Геометрический и физический смысл двойного интеграла. Основные свойства двойного интеграла.
- •4. Вычисление двойного интеграла в полярных координатах.
- •6. Тройной интеграл. Схема получения тройного интеграла.
- •1) Разбиваем область на «элементарных областей» .
- •3) Возьмем произвольную точку .
- •5) Составляем интегральную сумму
- •7. Основные свойства тройного интеграла (хотя бы 4 свойства). Формула вычисления тройного интеграла в декартовой системе координат.
- •3. Если область разбить линией на две области и такие, что , а пересечение , где линия, разделяющая и (см. Рисунок), то
- •8. Замена переменной в тройном интеграле. Вычисление тройного интеграла в цилиндрических координатах.
- •9. Замена переменной в тройном интеграле. Вычисление тройного интеграла в сферических координатах.
- •10. Некоторые приложения тройного интеграла в геометрии и физике.
- •11. Криволинейный интеграл I рода. Основные свойства кри-I.
- •12. Вычисление криволинейного интеграла I рода: явное представление кривой, параметрическое представление кривой, полярное представление кривой.
- •13. Некоторые приложения кри-I рода в геометрии и физике.
- •14. Криволинейный интеграл II рода. Основные свойства кри-II.
- •15. Вычисление кри-II: явное представление кривой, параметрическое представ-ление кривой. Некоторые приложения кри-II.
- •16. Формула Остроградского – Грина
- •17. Поверхностный интеграл I рода. Основные свойства поверхностного интеграла I рода. Вычисление поверхностного интеграла I рода.
- •3.2. Вычисление поверхностного интеграла I рода
- •18. Поверхностный интеграл II рода. Свойства поверхностного интеграла II рода.
- •19. Вычисление поверхностного интеграла II рода. Формула Остроградского - Гаусса для вычисления поверхностного интеграла II рода.
- •20. Скалярное поле. Производная по направлению. Градиент.
- •21. Векторное поле. Векторные (силовые) линии. Векторная трубка.
- •22. Поток векторного поля через поверхность. Формула вычисления потока векторного поля. Источник и сток. Формула Остроградского – Гаусса для вычисления потока.
- •23. Дивергенция поля. Ротор поля. Формула Стокса.
- •24. Циркуляция поля. Физический смысл циркуляции поля. Формула Стокса.
- •25. Векторные дифференциальные операции первого порядка. Оператор Гамильтона. Перечислить векторные дифференциальные операции второго порядка.
- •26. Классификация векторных полей: определения соленоидального, потенциального и гармонического векторного поля.
- •27. Числовой ряд. N-ая частичная сумма ряда. Сходимость и расходимость ряда. Некоторые свойства рядов. -ый остаток ряда.
- •28. Сформулировать и доказать необходимый признак сходимости ряда. Достаточ-ный признак расходимости ряда. Гармонический ряд.
- •29. Признаки сравнения рядов. Признак Даламбера.
- •30. Радикальный признак Коши. Интегральный признак Коши. Ряд Дирихле.
- •31. Знакочередующиеся ряды. Признак Лейбница. Абсолютная и условная сходимости рядов.
- •32. Функциональный ряд. Точка сходимости. Область сходимости функционального ряда. -ая частична сумма и -ый остаток функционального ряда.
- •33. Степенной ряд. Интервал и радиус сходимости степенного ряда.
- •34. Ряды Тейлора и Маклорена. Разложение функций в степенной ряд.
- •38. Теорема Дирихле. Разложение в ряд Фурье четных и нечетных функций.
- •39. Теорема Дирихле. Разложение в ряд Фурье функций произвольного периода.
23. Дивергенция поля. Ротор поля. Формула Стокса.
Дивергенцией (или расходимостью) векторного поля
в точке , обозначаемой символом , называется величина, равная сумме частных производных, вычисленных в точке т.е.
.
Отметим некоторые свойства дивергенции:
Если постоянный вектор, то .
, где .
, т.е. дивергенция суммы двух векторных функций равна сумме дивергенции слагаемых.
Если скалярная функция, а вектор, то
.
Сравнивая формулы (4.8) и (4.9) видим, что формулу Остроградского – Гаусса можно записать иначе:
.Формула означает:
поток векторного поля через замкнутую поверхность (в направлении внешней нормали) равен тройному интегралу от дивергенции этого поля по объему , ограниченному данной поверхностью.
Как видно из определения, дивергенция векторного поля в точке является скалярной величиной. Она образует скалярное поле в данном векторном поле.
Ротором (или вихрем) векторного поля
называется
вектор, который обозначается
![]() и определяется формулой
и определяется формулой
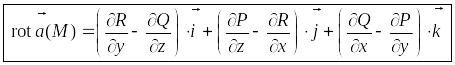 .
(4.13)
.
(4.13)
Формулу (4.13) можно записать с помощью символического определителя, который удобный для запоминания:
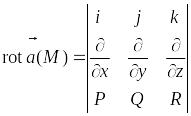
Отметим некоторые свойства ротора:
Если постоянный вектор, то
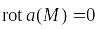 .
.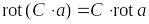 ,
где
.
,
где
.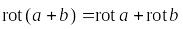 ,
т.е. ротор суммы двух векторных функций
равна сумме дивергенции слагаемых.
,
т.е. ротор суммы двух векторных функций
равна сумме дивергенции слагаемых.Если скалярная функция, а вектор, то
![]() .
.
Формула Стокса
Рассмотрим
в пространстве кусок двухсторонней
кусочно-гладкой поверхности ![]() ,
край которой образуется кусочно-гладкой
кривой
,
край которой образуется кусочно-гладкой
кривой ![]() .
Выберем положительную сторону поверхности
(из конца единичного вектора нормали
.
Выберем положительную сторону поверхности
(из конца единичного вектора нормали
![]() обход
границы представляется против часовой
стрелки). Для циркуляции векторного
поля
обход
границы представляется против часовой
стрелки). Для циркуляции векторного
поля ![]() вдоль контура границы имеет место
формула Стокса:
вдоль контура границы имеет место
формула Стокса: 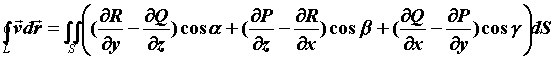 ,
где
,
где ![]() -
компоненты векторного поля,
-
компоненты векторного поля, ![]() -
направляющие косинусы вектора нормали.
-
направляющие косинусы вектора нормали.
Эту же формулу Стокса можно записать и векторной форме:
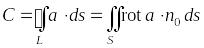 .
(4.15)
.
(4.15)
Формула
(4.15) означает следующее: циркуляция
векторного поля
вдоль
замкнутого контура
![]() равна потоку ротора этого поля через
любую гладкую поверхность
,
краем которой является контур
.
Направление обхода по контуру
и сторона поверхности
одновременно или положительные, или
отрицательные.
равна потоку ротора этого поля через
любую гладкую поверхность
,
краем которой является контур
.
Направление обхода по контуру
и сторона поверхности
одновременно или положительные, или
отрицательные.
24. Циркуляция поля. Физический смысл циркуляции поля. Формула Стокса.
Циркуляцией вектора вдоль замкнутого контура называется криволинейный интеграл по этому контуру от скалярного произведения вектора
на вектор
![]() ,
касательной к контуру, т.е.
,
касательной к контуру, т.е.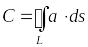 .
.
Циркуляцию вектора можно находить по другой формуле
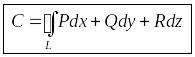 .
.
Циркуляция
![]() ,
имеет простой физический
смысл: если
кривая
расположена в силовом поле, то циркуляция
– это работа силы
поля при перемещении материальной точки
вдоль
.Отметим,
что вдоль замкнутых векторных линий
циркуляция отлична от нуля, потому что
в каждой точке векторной линии скалярное
произведение
,
имеет простой физический
смысл: если
кривая
расположена в силовом поле, то циркуляция
– это работа силы
поля при перемещении материальной точки
вдоль
.Отметим,
что вдоль замкнутых векторных линий
циркуляция отлична от нуля, потому что
в каждой точке векторной линии скалярное
произведение
![]() сохраняет знак: положительный, если
направление вектора
совпадает с направлением обхода векторной
линии; отрицательный – в противном
случае.
сохраняет знак: положительный, если
направление вектора
совпадает с направлением обхода векторной
линии; отрицательный – в противном
случае.
Формула Стокса
Рассмотрим в пространстве кусок двухсторонней кусочно-гладкой поверхности , край которой образуется кусочно-гладкой кривой . Выберем положительную сторону поверхности (из конца единичного вектора нормали обход границы представляется против часовой стрелки). Для циркуляции векторного поля вдоль контура границы имеет место формула Стокса: , где - компоненты векторного поля, - направляющие косинусы вектора нормали.
Эту же формулу Стокса можно записать и векторной форме:
. (4.15)
Формула (4.15) означает следующее: циркуляция векторного поля вдоль замкнутого контура равна потоку ротора этого поля через любую гладкую поверхность , краем которой является контур . Направление обхода по контуру и сторона поверхности одновременно или положительные, или отрицательные.
