
- •2. Геометрический и физический смысл двойного интеграла. Основные свойства двойного интеграла.
- •4. Вычисление двойного интеграла в полярных координатах.
- •6. Тройной интеграл. Схема получения тройного интеграла.
- •1) Разбиваем область на «элементарных областей» .
- •3) Возьмем произвольную точку .
- •5) Составляем интегральную сумму
- •7. Основные свойства тройного интеграла (хотя бы 4 свойства). Формула вычисления тройного интеграла в декартовой системе координат.
- •3. Если область разбить линией на две области и такие, что , а пересечение , где линия, разделяющая и (см. Рисунок), то
- •8. Замена переменной в тройном интеграле. Вычисление тройного интеграла в цилиндрических координатах.
- •9. Замена переменной в тройном интеграле. Вычисление тройного интеграла в сферических координатах.
- •10. Некоторые приложения тройного интеграла в геометрии и физике.
- •11. Криволинейный интеграл I рода. Основные свойства кри-I.
- •12. Вычисление криволинейного интеграла I рода: явное представление кривой, параметрическое представление кривой, полярное представление кривой.
- •13. Некоторые приложения кри-I рода в геометрии и физике.
- •14. Криволинейный интеграл II рода. Основные свойства кри-II.
- •15. Вычисление кри-II: явное представление кривой, параметрическое представ-ление кривой. Некоторые приложения кри-II.
- •16. Формула Остроградского – Грина
- •17. Поверхностный интеграл I рода. Основные свойства поверхностного интеграла I рода. Вычисление поверхностного интеграла I рода.
- •3.2. Вычисление поверхностного интеграла I рода
- •18. Поверхностный интеграл II рода. Свойства поверхностного интеграла II рода.
- •19. Вычисление поверхностного интеграла II рода. Формула Остроградского - Гаусса для вычисления поверхностного интеграла II рода.
- •20. Скалярное поле. Производная по направлению. Градиент.
- •21. Векторное поле. Векторные (силовые) линии. Векторная трубка.
- •22. Поток векторного поля через поверхность. Формула вычисления потока векторного поля. Источник и сток. Формула Остроградского – Гаусса для вычисления потока.
- •23. Дивергенция поля. Ротор поля. Формула Стокса.
- •24. Циркуляция поля. Физический смысл циркуляции поля. Формула Стокса.
- •25. Векторные дифференциальные операции первого порядка. Оператор Гамильтона. Перечислить векторные дифференциальные операции второго порядка.
- •26. Классификация векторных полей: определения соленоидального, потенциального и гармонического векторного поля.
- •27. Числовой ряд. N-ая частичная сумма ряда. Сходимость и расходимость ряда. Некоторые свойства рядов. -ый остаток ряда.
- •28. Сформулировать и доказать необходимый признак сходимости ряда. Достаточ-ный признак расходимости ряда. Гармонический ряд.
- •29. Признаки сравнения рядов. Признак Даламбера.
- •30. Радикальный признак Коши. Интегральный признак Коши. Ряд Дирихле.
- •31. Знакочередующиеся ряды. Признак Лейбница. Абсолютная и условная сходимости рядов.
- •32. Функциональный ряд. Точка сходимости. Область сходимости функционального ряда. -ая частична сумма и -ый остаток функционального ряда.
- •33. Степенной ряд. Интервал и радиус сходимости степенного ряда.
- •34. Ряды Тейлора и Маклорена. Разложение функций в степенной ряд.
- •38. Теорема Дирихле. Разложение в ряд Фурье четных и нечетных функций.
- •39. Теорема Дирихле. Разложение в ряд Фурье функций произвольного периода.
21. Векторное поле. Векторные (силовые) линии. Векторная трубка.
Если
каждой точке
области
соответствует некоторый вектор
![]() ,
то говорят, что задано векторное
поле или
векторная
функция точки.Вектор
,
определяющий векторное поле, можно
рассматривать как векторную функцию
трех скалярных аргументов
,
то говорят, что задано векторное
поле или
векторная
функция точки.Вектор
,
определяющий векторное поле, можно
рассматривать как векторную функцию
трех скалярных аргументов
![]() ,
т.е.
,
т.е.
![]() .Вектор
можно представить, разложив его по ортам
координатных осей, в виде:
.Вектор
можно представить, разложив его по ортам
координатных осей, в виде:
![]() ,
,
где
![]()
проекции вектора
проекции вектора
![]() на оси координат, а также скалярные
функции, которые непрерывны со своими
частными производными. Простейшими
геометрическими характеристиками
векторного поля являются векторные
линии.
на оси координат, а также скалярные
функции, которые непрерывны со своими
частными производными. Простейшими
геометрическими характеристиками
векторного поля являются векторные
линии.
Векторной (силовой) линией поля называется линия, касательная к которой в каждой точке имеет направление соответствующего ей вектора .Совокупность всех векторных линий поля, проходящих через некоторую замкнутую кривую, называется векторной трубкой.
Изучение векторного поля обычно начинается с изучения расположения его векторных линий. Векторные линии поля
описываются системой дифференциальных уравнений
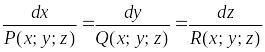 .
.
22. Поток векторного поля через поверхность. Формула вычисления потока векторного поля. Источник и сток. Формула Остроградского – Гаусса для вычисления потока.
Потоком
вектора
через
поверхность
![]() называется интеграл по поверхности от
скалярного произведения вектора поля
на единичный вектор нормали к поверхности,
т.е.
называется интеграл по поверхности от
скалярного произведения вектора поля
на единичный вектор нормали к поверхности,
т.е.
![]() .
.
Таким
образом, вычисление потока вектора
сводится к вычислению интеграла по
поверхности. Из самого определения
следует, что поток вектора П
величина скалярная. Если изменить
направление нормали
![]() на противоположный, т.е. переменить
сторону поверхности
,
то поток П
изменит знак.
на противоположный, т.е. переменить
сторону поверхности
,
то поток П
изменит знак.
Так
как
![]() ,
то
,
то
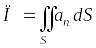 ,где
,где
![]()
проекция вектора
проекция вектора
![]() на направление нормали
,
на направление нормали
,
![]()
дифференциал (элемент) площадки
поверхности.
дифференциал (элемент) площадки
поверхности.
Поскольку
,
![]() ,
то поток (4.5) вектора
можно записать в виде
,
то поток (4.5) вектора
можно записать в виде
![]() ,
,
или в виде
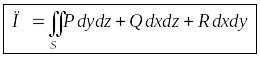 .
.
Особый
интерес представляет случай, когда
поверхность замкнута и ограничивает
некоторый объем
.
Тогда поток вектора записывается в виде
![]() .
В этом случае за направление вектора
обычно берут направление внешней нормали
и говорят о потоке изнутри поверхности
.
.
В этом случае за направление вектора
обычно берут направление внешней нормали
и говорят о потоке изнутри поверхности
.
Дивергенцией (или расходимостью) векторного поля
![]()
в
точке
,
обозначаемой символом
![]() ,
называется величина, равная сумме
частных производных, вычисленных в
точке
т.е.
,
называется величина, равная сумме
частных производных, вычисленных в
точке
т.е.
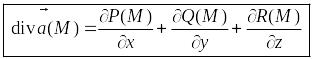 .
.
Отметим некоторые свойства дивергенции:
Если постоянный вектор, то
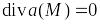 .
.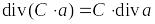 ,
где
,
где
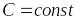 .
.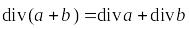 ,
т.е. дивергенция суммы двух векторных
функций равна сумме дивергенции
слагаемых.
,
т.е. дивергенция суммы двух векторных
функций равна сумме дивергенции
слагаемых.Если
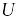
скалярная функция, а
вектор, то
скалярная функция, а
вектор, то
![]() .
.
Сравнивая формулы (4.8) и (4.9) видим, что формулу Остроградского – Гаусса можно записать иначе:
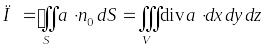 .Формула
означает:
.Формула
означает:
поток векторного поля через замкнутую поверхность (в направлении внешней нормали) равен тройному интегралу от дивергенции этого поля по объему , ограниченному данной поверхностью.
Как видно из определения, дивергенция векторного поля в точке является скалярной величиной. Она образует скалярное поле в данном векторном поле.
