19. Вычисление поверхностного интеграла II рода. Формула Остроградского - Гаусса для вычисления поверхностного интеграла II рода.

Вычисление поверхностного интеграла II рода сводится к вычислению двойного интеграла по плоской области.

Справедлива следующая формула, сводящая вычисление интеграла (3.4) к вычислению двойного интеграла:

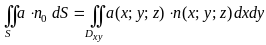. (3.5)

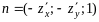
где  проекции поверхности на плоскость ,  нормальный вектор к поверхности , которая задана функцией 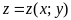. Причем в двойном интеграле переменную надо заменить на .

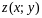Поверхностный интеграл II рода в формуле (3.4) можно записать иначе:

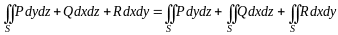. (3.6)

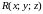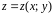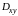
Пусть функция непрерывна во всех точках поверхности , которая задана непрерывной функцией в замкнутой области  проекции поверхности на плоскость . Тогда справедлива следующая формула:

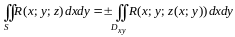. (3.7)

При этом перед двойным интегралом берется знак «+», если 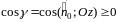, и знак «», если .

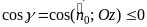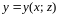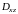
Если поверхность задана непрерывной функцией в замкнутой области  проекции поверхности на плоскость . Тогда справедлива следующая формула:

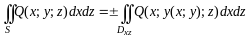. (3.8)

При этом перед двойным интегралом берется знак «+», если 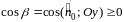, и знак «», если .

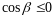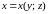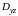
Если поверхность задана непрерывной функцией в замкнутой области  проекции поверхности на плоскость . Тогда справедлива следующая формула:

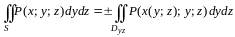. (3.9)

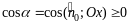При этом перед двойным интегралом берется знак «+», если , и знак «», если .

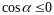Если  замкнутая гладкая поверхность, ограничивающая область , а  функции непрерывные со своими частными производными первого порядка в замкнутой области , то справедлива следующая формула:

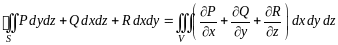. (3.10)

Формула (3.10) называется формулой Остроградского – Гаусса.

Эта формула позволяет упростить вычисление многих поверхностных интегралов.

20. Скалярное поле. Производная по направлению. Градиент.

Полем называется область пространства, в каждой точке которой определено значение некоторой величины.Если каждой точке этой области определено число , говорят, что в области определено (задано) скалярное поле или функция точки. Иначе можно сказать, что скалярное поле – это скалярная функция вместе с ее областью определения.

Пусть задано скалярное поле, т.е. задана функция, и точка . Будем предполагать, что функция непрерывна и имеет непрерывные производные по своим аргументам в области .

Производной от функции в точке по направлению вектора называется предел отношения при , т.е. .

Если функция дифференцируемая, то производная от функции в точке по направлению вектора находится по следующей формуле:

,

где  направляющие косинусы вектора .

В случае функции двух переменных , т.е. когда поле плоское, формула (4.1) примет следующий вид:

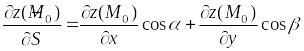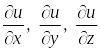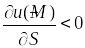, где .Подобно тому, как частные производные характеризуют скорость изменения функции в направлении осей координат, так и производная по направлению будет являться скоростью изменения функции в точке по направлению вектора . Если , то функция возрастает в направлении , если , то функция убывает в направлении .

Градиент

В каждой точке области , в которой задана скалярная функция , определим вектор, проекциями которого на оси координат являются значения частных производных в выбранной точке . Назовем этот вектор градиентом функции и обозначим его символами или (набла-оператор, записываемый в виде «вектора» с компонентами ).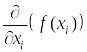

Градиентом функции в точке называется вектор, проекции которого служат значения частных производных этой функции, т.е.

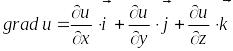. (4.3)

Подчеркнем, что проекции градиента зависят от выбора точки и изменяются с изменением координат этой точки. Таким образом, каждой точке скалярного поля, определяемого функцией , соответствует определенный вектор – градиент этой функции. Отметим, что градиент линейной функции есть постоянный вектор .

Используя определение градиента, формуле для производной по направлению можно придать следующий вид:

,которая читается так: производная функции по данному направлению равна скалярному произведению градиента функции на единичный вектор этого направления ( ).Учитывая то, что скалярное произведение равно модулю одного вектора умноженному на проекцию другого вектора на направление первого, то можно еще сказать, что: производная функции по данному направлению равна проекции градиента функции на направление дифференцирования, т.е.

,

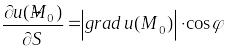где   угол между и направлением .