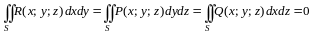- •2. Геометрический и физический смысл двойного интеграла. Основные свойства двойного интеграла.
- •4. Вычисление двойного интеграла в полярных координатах.
- •6. Тройной интеграл. Схема получения тройного интеграла.
- •1) Разбиваем область на «элементарных областей» .
- •3) Возьмем произвольную точку .
- •5) Составляем интегральную сумму
- •7. Основные свойства тройного интеграла (хотя бы 4 свойства). Формула вычисления тройного интеграла в декартовой системе координат.
- •3. Если область разбить линией на две области и такие, что , а пересечение , где линия, разделяющая и (см. Рисунок), то
- •8. Замена переменной в тройном интеграле. Вычисление тройного интеграла в цилиндрических координатах.
- •9. Замена переменной в тройном интеграле. Вычисление тройного интеграла в сферических координатах.
- •10. Некоторые приложения тройного интеграла в геометрии и физике.
- •11. Криволинейный интеграл I рода. Основные свойства кри-I.
- •12. Вычисление криволинейного интеграла I рода: явное представление кривой, параметрическое представление кривой, полярное представление кривой.
- •13. Некоторые приложения кри-I рода в геометрии и физике.
- •14. Криволинейный интеграл II рода. Основные свойства кри-II.
- •15. Вычисление кри-II: явное представление кривой, параметрическое представ-ление кривой. Некоторые приложения кри-II.
- •16. Формула Остроградского – Грина
- •17. Поверхностный интеграл I рода. Основные свойства поверхностного интеграла I рода. Вычисление поверхностного интеграла I рода.
- •3.2. Вычисление поверхностного интеграла I рода
- •18. Поверхностный интеграл II рода. Свойства поверхностного интеграла II рода.
- •19. Вычисление поверхностного интеграла II рода. Формула Остроградского - Гаусса для вычисления поверхностного интеграла II рода.
- •20. Скалярное поле. Производная по направлению. Градиент.
- •21. Векторное поле. Векторные (силовые) линии. Векторная трубка.
- •22. Поток векторного поля через поверхность. Формула вычисления потока векторного поля. Источник и сток. Формула Остроградского – Гаусса для вычисления потока.
- •23. Дивергенция поля. Ротор поля. Формула Стокса.
- •24. Циркуляция поля. Физический смысл циркуляции поля. Формула Стокса.
- •25. Векторные дифференциальные операции первого порядка. Оператор Гамильтона. Перечислить векторные дифференциальные операции второго порядка.
- •26. Классификация векторных полей: определения соленоидального, потенциального и гармонического векторного поля.
- •27. Числовой ряд. N-ая частичная сумма ряда. Сходимость и расходимость ряда. Некоторые свойства рядов. -ый остаток ряда.
- •28. Сформулировать и доказать необходимый признак сходимости ряда. Достаточ-ный признак расходимости ряда. Гармонический ряд.
- •29. Признаки сравнения рядов. Признак Даламбера.
- •30. Радикальный признак Коши. Интегральный признак Коши. Ряд Дирихле.
- •31. Знакочередующиеся ряды. Признак Лейбница. Абсолютная и условная сходимости рядов.
- •32. Функциональный ряд. Точка сходимости. Область сходимости функционального ряда. -ая частична сумма и -ый остаток функционального ряда.
- •33. Степенной ряд. Интервал и радиус сходимости степенного ряда.
- •34. Ряды Тейлора и Маклорена. Разложение функций в степенной ряд.
- •38. Теорема Дирихле. Разложение в ряд Фурье четных и нечетных функций.
- •39. Теорема Дирихле. Разложение в ряд Фурье функций произвольного периода.
15. Вычисление кри-II: явное представление кривой, параметрическое представ-ление кривой. Некоторые приложения кри-II.
Вычисление КРИ-II, как и КРИ-I, может быть сведено к вычислению определенного интеграла.
Явное представление кривой
Если
кривая
лежит в плоскости
и
задана уравнением
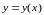 ,
производная
,
производная
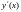 непрерывна на
непрерывна на
 ,
,
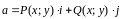 ,
то
,
то
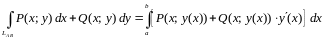 .
.
Параметрическое представление кривой
Если
гладкая кривая
задана параметрическими уравнениями
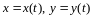 ,
,
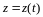 ,
где
,
где
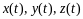
непрерывно дифференцируемые функции,
непрерывно дифференцируемые функции,
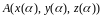 и
и
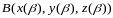
соответственно начальная и конечная
точки этой кривой, то верна следующая
формула для вычисления КРИ-II:
соответственно начальная и конечная
точки этой кривой, то верна следующая
формула для вычисления КРИ-II:
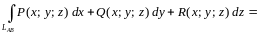

Если
кривая
лежит в плоскости
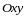 ,
,
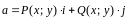 ,
то формула упрощается
,
то формула упрощается
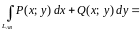
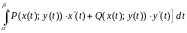
Площадь плоской фигуры
Площадь
 плоской фигуры, расположенной в плоскости
плоской фигуры, расположенной в плоскости
 и ограниченной замкнутой линией
,
можно найти по формуле
и ограниченной замкнутой линией
,
можно найти по формуле
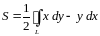 ,
,
при этом кривая , делает обход против часовой стрелки.
Работа переменной силы
Переменная
сила
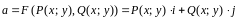 на криволинейном участке
производит работу, которая находится
по формуле
на криволинейном участке
производит работу, которая находится
по формуле
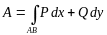
16. Формула Остроградского – Грина
Если
функции
 и
и
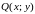 непрерывны и имеют непрерывные частные
производные в замкнутой односвязной
области
непрерывны и имеют непрерывные частные
производные в замкнутой односвязной
области
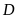 ,
лежащей в плоскости
,
лежащей в плоскости
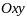 и ограниченной кусочно-гладкой кривой
и ограниченной кусочно-гладкой кривой
 ,
то
,
то
 ,
(2.10)
,
(2.10)
где
интегрирование по контуру
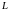 выполняется в положительном направлении.
выполняется в положительном направлении.
Формулу (2.10) называется формулой Остроградского – Грина.
17. Поверхностный интеграл I рода. Основные свойства поверхностного интеграла I рода. Вычисление поверхностного интеграла I рода.
Если
при
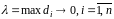 и
и
 интегральная сумма
интегральная сумма
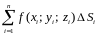 имеет предел, то он называется поверхностным
интегралом I
рода от
функции
имеет предел, то он называется поверхностным
интегралом I
рода от
функции
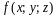 по поверхности
и обозначается
по поверхности
и обозначается
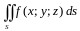 .
.
Таким образом, по определению,
 .
(3.1)
.
(3.1)
Основные свойства поверхностного интеграла I рода
1.
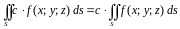 ,
где
,
где
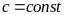 .
.
2.
 .
.
3.
Если поверхность
разбить на части
 и
и
 такие, что
такие, что
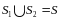 ,
а пересечение
и
состоит лишь из границы, их разделяющей,
то
,
а пересечение
и
состоит лишь из границы, их разделяющей,
то
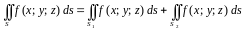 .
.
4.
Если на поверхности
функции
 и
и
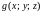 удовлетворяют неравенству
удовлетворяют неравенству
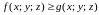 ,
то и
,
то и
 .
.
5.
Если
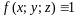 ,
то
,
то
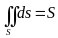 ,
где
площадь поверхности
.
,
где
площадь поверхности
.
6.
(Теорема о среднем) Если функция
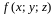 непрерывна на поверхности
,
то на этой поверхности существует такая
точка
непрерывна на поверхности
,
то на этой поверхности существует такая
точка
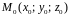 ,
что
,
что
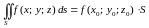 .
.
3.2. Вычисление поверхностного интеграла I рода
Вычисление
поверхностного интеграла I
рода сводится к вычислению двойного
интеграла по области
проекции поверхности
на плоскости
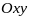 .
.
Если
поверхность
задана уравнением
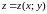 ,
то поверхностный интеграл I
рода вычисляется по следующей формуле:
,
то поверхностный интеграл I
рода вычисляется по следующей формуле:
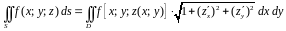 ,
(3.2)
,
(3.2)
где проекция поверхности на координатную плоскость .
Если
поверхность
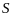 задана уравнениями вида
задана уравнениями вида
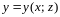 или
или
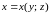 ,
то получаем следующие формулы
,
то получаем следующие формулы
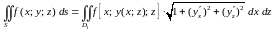
и
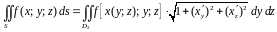 ,
,
где
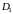 и
и

проекции поверхности
на координатную плоскость
и
соответственно.
проекции поверхности
на координатную плоскость
и
соответственно.
18. Поверхностный интеграл II рода. Свойства поверхностного интеграла II рода.
Предел
интегральной суммы, найденный при
условии, что
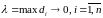 ,
,
 ,
называется поверхностным
интегралом второго рода
от вектор-функции
,
называется поверхностным
интегралом второго рода
от вектор-функции
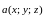 по поверхности
и обозначается
по поверхности
и обозначается
 .
.
Таким образом, по определению
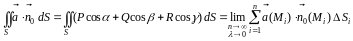
Свойства поверхностного интеграла II рода
Поверхностный интеграл II рода изменяет знак при перемене стороны поверхности.
Постоянный множитель можно вынести за знак поверхностного интеграла.
Поверхностный интеграл от суммы функций равен сумме соответствующих интегралов от слагаемых.
Поверхностный интеграл II рода по всей поверхности
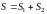 равен сумме интегралов по ее частям
равен сумме интегралов по ее частям
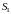 и
и
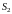 (аддитивное свойство), если
и
пересекаются лишь по границе, их
разделяющей.
(аддитивное свойство), если
и
пересекаются лишь по границе, их
разделяющей.
Если , и
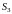
цилиндрические поверхности с образующими,
параллельными соответственно осям
цилиндрические поверхности с образующими,
параллельными соответственно осям
 ,
то
,
то