6. Тройной интеграл. Схема получения тройного интеграла.

Схема получения тройного интеграла

1) Разбиваем область на «элементарных областей» .

2) Объем «элементарной области» 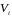обозначим 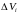, а диаметр (наибольшее расстояние между двумя точками области) – через .

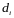3) Возьмем произвольную точку .

4) Находим .

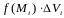5) Составляем интегральную сумму

.

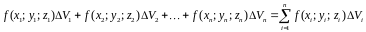6) Обозначим через 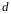длину наибольшего из диаметров «элементарных областей», т.е. 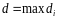, 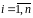. Найдем предел интегральной суммы, когда 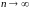так, что .

.

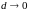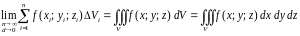Предел интегральной суммы, когда число «элементарных областей» неограниченно возрастает, а длина наибольшего диаметра стремится к нулю, называется тройным интегралом от 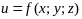на замкнутой областью .

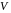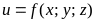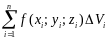Таким образом, тройным интегралом от по замкнутой областью называется предел интегральной суммы , когда число «элементарных областей» неограниченно возрастает, а длина наибольшего диаметра стремится к нулю:

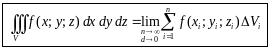. (1.7)

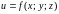 интегрируемая функция в области ;

 область интегрирования;

, и  переменные интегрирования;

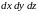или  элемент объема.

7. Основные свойства тройного интеграла (хотя бы 4 свойства). Формула вычисления тройного интеграла в декартовой системе координат.

Свойства:

1. 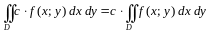, где .

2.

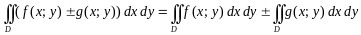
3. Если область разбить линией на две области и такие, что , а пересечение , где  линия, разделяющая и (см. Рисунок), то

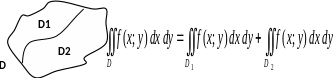
4. Если в области имеет место неравенство , то и

.

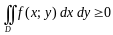5. Если в области функции и 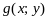удовлетворяют неравенству 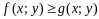, то и

.

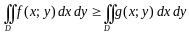Тогда тройной интеграл в декартовых координатах вычисляется по следующей формуле:

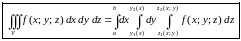. (1.8)

8. Замена переменной в тройном интеграле. Вычисление тройного интеграла в цилиндрических координатах.

При вычислении тройного интеграла, как и для двойного, часто применяется метод подстановки, т.е. совершается преобразование переменных.

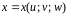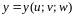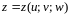Пусть совершается подстановка , и . Если эти функции имеют в некоторой области 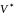пространства непрерывные частные производные и отличный от нуля определитель

,

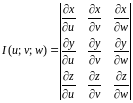то справедлива формула замены переменной в тройном интеграле:

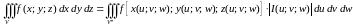
(1.9)

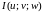
Здесь  определитель Якоби, или якобиан преобразования (примем без доказательства)

Вычисление тройного интеграла

в цилиндрических координатах

Для вычисления тройного интеграла часто используют так называемые цилиндрические координаты.

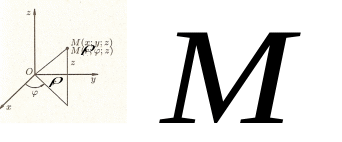
Цилиндрические координаты точки связаны с ее декартовыми координатами следующими соотношениями: 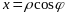, , 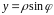, 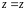где .

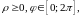
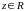Возьмем в качестве 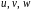цилиндрические координаты 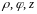и вычислим якобиан преобразования:

.

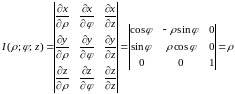Формула замены переменных (1.9) принимает вид:

.

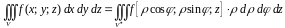9. Замена переменной в тройном интеграле. Вычисление тройного интеграла в сферических координатах.

Вычисление тройного интеграла

в сферических координатах

В некоторых случаях вычисление тройного интеграла удобно производить, перейдя к сферическим координатам.

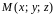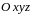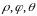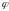
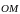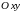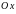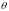
Сферическими координатами точки пространства называется тройка чисел , где  длина радиус-вектора точки ,  угол, образованный проекцией радиус-вектора на плоскость и осью ,  угол отклонения радиус-вектора от оси 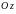(см. рис.).

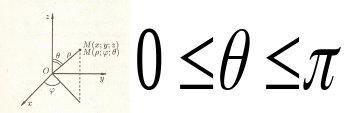
Возьмем в качестве 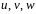сферические координаты 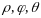и вычислим якобиан преобразования:

.

Формула замены переменных (1.9) принимает вид:

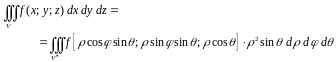. (1.11)

Переходить к сферическим координатам удобно, когда область интегрирования 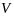есть шар (равнение его границы 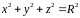в сферических координатах 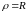имеет вид ) или его часть, а также, если подынтегральная функция имеет вид .
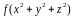