4. Вычисление двойного интеграла в полярных координатах.

Вычисление двойного интеграла

в полярных координатах

При вычислении определенного интеграла важную роль играет правило замены переменной, согласно которому при соблюдении соответствующих условий получаем

.

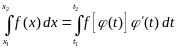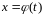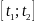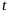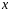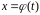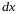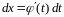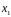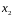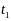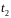Обычно функция монотонна. Она осуществляет взаимно однозначное соответствие между точками промежутка изменения переменной и точками промежутка изменения переменной . Делая замену по формуле , необходимо заменить на и вместо старых пределов и по переменной взять им соответствующие новые пределы и по переменной .

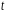Для упрощенного вычисления двойного интеграла также применяется метод подстановки. Но правило замены переменной в двойном интеграле значительно сложнее, чем в определенном интеграле. Приведем только окончательную формулу замены переменных в двойном интеграле и разъясним ее на примере преобразования к полярным координатам.

Определим преобразование независимых переменных и как

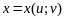и .

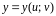Если функци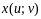и и 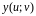имеют в некоторой области плоскости непрерывные частные производные первого порядка и отличный от нуля определитель

,

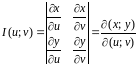а функция непрерывна в области , то справедлива формула замены переменной в двойном интеграле:

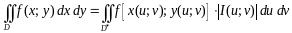. (1.4)

Сами новые переменные и называются криволинейными координатами. Различные системы криволинейных координат играют важную роль в математике и ее приложениях.

Функциональный определитель называется определителем Якоби или якобианом (Г. Якоби (1804 – 1851) – немецкий математик).

Рассмотрим частный случай замены переменных, часто используемый при вычислении двойного интеграла, а именно замену декартовых координат и полярными координатам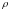и и .

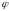В качестве переменных и возьмем полярные координаты и . Они связаны с декартовыми координатами формулами , .

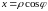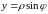Правые части в этих равенствах – непрерывно дифференцируемые функции. Якобиан преобразования определяется как

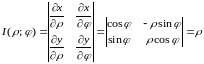
Формула замены переменных (1.4) принимает вид:

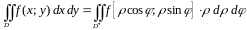, (1.5)

где  область в полярной системе координат, соответствующая области в декартовой системе координат.

5. Приложения двойного интеграла в геометрии и физике.

Объем такого цилиндра численно равен площади основания 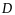, т.е. площади области интегрирования . Тогда для вычисления площади плоской фигуры получаем формулы:

1. для вычисления в декартовой системе координат: ;

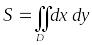2. для вычисления в полярной системе координат: .

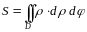Масса плоской фигуры

Согласно физическому смыслу двойного интеграла, масса плоской пластины находится по формуле:

,

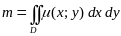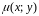
где  плотность этой пластины.

Статистические моменты плоской фигуры

Статистические моменты плоской фигуры относительно осе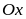й и 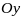могут быть вычислены по формулам:

;

.

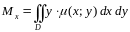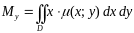Координаты центра масс

Координаты плоской фигуры вычисляются по следующим формулам:

;

.

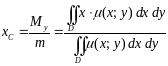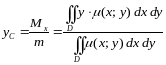Моменты инерции плоской фигуры

Моментом инерции материальной точки массы 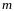относительно оси 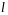называется произведение массы на квадрат расстояния 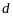точки до оси, т.е. .

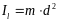Моменты инерции плоской фигуры относительно осей и могут быть вычислены по формулам:

;

.

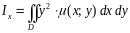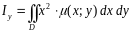Момент инерции плоской фигуры относительно начала координат вычисляется по следующей формуле:

.
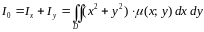