
- •2. Геометрический и физический смысл двойного интеграла. Основные свойства двойного интеграла.
- •4. Вычисление двойного интеграла в полярных координатах.
- •6. Тройной интеграл. Схема получения тройного интеграла.
- •1) Разбиваем область на «элементарных областей» .
- •3) Возьмем произвольную точку .
- •5) Составляем интегральную сумму
- •7. Основные свойства тройного интеграла (хотя бы 4 свойства). Формула вычисления тройного интеграла в декартовой системе координат.
- •3. Если область разбить линией на две области и такие, что , а пересечение , где линия, разделяющая и (см. Рисунок), то
- •8. Замена переменной в тройном интеграле. Вычисление тройного интеграла в цилиндрических координатах.
- •9. Замена переменной в тройном интеграле. Вычисление тройного интеграла в сферических координатах.
- •10. Некоторые приложения тройного интеграла в геометрии и физике.
- •11. Криволинейный интеграл I рода. Основные свойства кри-I.
- •12. Вычисление криволинейного интеграла I рода: явное представление кривой, параметрическое представление кривой, полярное представление кривой.
- •13. Некоторые приложения кри-I рода в геометрии и физике.
- •14. Криволинейный интеграл II рода. Основные свойства кри-II.
- •15. Вычисление кри-II: явное представление кривой, параметрическое представ-ление кривой. Некоторые приложения кри-II.
- •16. Формула Остроградского – Грина
- •17. Поверхностный интеграл I рода. Основные свойства поверхностного интеграла I рода. Вычисление поверхностного интеграла I рода.
- •3.2. Вычисление поверхностного интеграла I рода
- •18. Поверхностный интеграл II рода. Свойства поверхностного интеграла II рода.
- •19. Вычисление поверхностного интеграла II рода. Формула Остроградского - Гаусса для вычисления поверхностного интеграла II рода.
- •20. Скалярное поле. Производная по направлению. Градиент.
- •21. Векторное поле. Векторные (силовые) линии. Векторная трубка.
- •22. Поток векторного поля через поверхность. Формула вычисления потока векторного поля. Источник и сток. Формула Остроградского – Гаусса для вычисления потока.
- •23. Дивергенция поля. Ротор поля. Формула Стокса.
- •24. Циркуляция поля. Физический смысл циркуляции поля. Формула Стокса.
- •25. Векторные дифференциальные операции первого порядка. Оператор Гамильтона. Перечислить векторные дифференциальные операции второго порядка.
- •26. Классификация векторных полей: определения соленоидального, потенциального и гармонического векторного поля.
- •27. Числовой ряд. N-ая частичная сумма ряда. Сходимость и расходимость ряда. Некоторые свойства рядов. -ый остаток ряда.
- •28. Сформулировать и доказать необходимый признак сходимости ряда. Достаточ-ный признак расходимости ряда. Гармонический ряд.
- •29. Признаки сравнения рядов. Признак Даламбера.
- •30. Радикальный признак Коши. Интегральный признак Коши. Ряд Дирихле.
- •31. Знакочередующиеся ряды. Признак Лейбница. Абсолютная и условная сходимости рядов.
- •32. Функциональный ряд. Точка сходимости. Область сходимости функционального ряда. -ая частична сумма и -ый остаток функционального ряда.
- •33. Степенной ряд. Интервал и радиус сходимости степенного ряда.
- •34. Ряды Тейлора и Маклорена. Разложение функций в степенной ряд.
- •38. Теорема Дирихле. Разложение в ряд Фурье четных и нечетных функций.
- •39. Теорема Дирихле. Разложение в ряд Фурье функций произвольного периода.
30. Радикальный признак Коши. Интегральный признак Коши. Ряд Дирихле.
Теорема 1.6 (радикальный признак Коши). Пусть дан ряд (1.1) с положительными членами и существует конечный или бесконечный предел
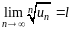 .
.
Тогда:
при
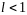 ряд сходится;
ряд сходится;при
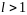 ряд расходится.
ряд расходится.
При радикальный признак Коши не дает ответа на вопрос о сходимости или расходимости ряда. В этом случае сходимость ряда исследуется с помощью других признаков.
Теорема 1.7 (интегральный признак Коши). Пусть дан ряд
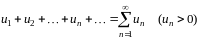 ,
,
члены
которого являются значениями непрерывной
положительной функции
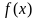 при целых значениях аргумента
при целых значениях аргумента
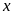 :
:
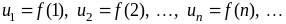 ,
,
и
пусть
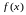 монотонно убывает на промежутке
монотонно убывает на промежутке
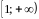 .
Тогда ряд сходится, если сходится
несобственный интеграл
.
Тогда ряд сходится, если сходится
несобственный интеграл
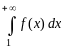 ,
и расходится, если несобственный интеграл
,
и расходится, если несобственный интеграл
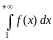 расходится.
расходится.
Надо
отметить, что вместо интеграла
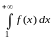 можно брать интеграл
можно брать интеграл
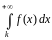 ,
где
,
где
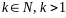 .
Отбрасывание
.
Отбрасывание
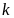 первых членов ряда, как известно, не
влияет на сходимость (расходимость)
ряда.
первых членов ряда, как известно, не
влияет на сходимость (расходимость)
ряда.
Пример 1.11. Исследовать на сходимость ряд
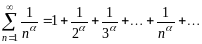 ,
(1.10)
,
(1.10)
где
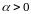
действительное число, ряд называется
обобщенным
гармоническим рядом
или рядом
Дирихле.
действительное число, ряд называется
обобщенным
гармоническим рядом
или рядом
Дирихле.
31. Знакочередующиеся ряды. Признак Лейбница. Абсолютная и условная сходимости рядов.
Знакочередующимся рядом называется ряд вида
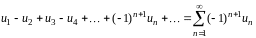 ,
(2.1)
,
(2.1)
где
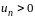 для всех
для всех
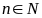 (т.е. ряд, положительные и отрицательные
члены которого следуют друг за другом
поочередно).
(т.е. ряд, положительные и отрицательные
члены которого следуют друг за другом
поочередно).
Для знакочередующихся рядов имеет место достаточный признак сходимости, установленный в 1714 г. Лейбницем в письме к И.Бернулли.
Теорема 2.1 (признак Лейбница). Знакочередующийся ряд (2.1) сходится, если
последовательность абсолютных величин ряда монотонно убывает, т.е.
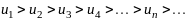 ;
;
общий член ряда стремится к нулю, т.е.
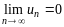 .
.
При
этом сумма
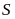 ряда (2.1) удовлетворяет неравенствам
ряда (2.1) удовлетворяет неравенствам
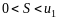 .
.
Знакопеременный ряд называется абсолютно сходящимся, если ряд, составленный из модулей его членов, сходится.
Знакопеременный ряд называется условно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов, расходится.
32. Функциональный ряд. Точка сходимости. Область сходимости функционального ряда. -ая частична сумма и -ый остаток функционального ряда.
Пусть
функции
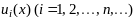 определены в области
определены в области
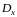 .
Тогда выражение вида
.
Тогда выражение вида
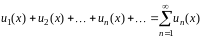 (3.1)
(3.1)
называется функциональным рядом.
Придавая
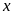 определенные значения
определенные значения
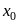 ,
получаем числовой ряд
,
получаем числовой ряд
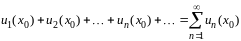 ,
,
который может быть как сходящимся, так и расходящимся.
Определение
3.2. Если
числовой ряд
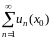 сходится при
сходится при
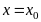 ,
то ряд называется сходящимся
в точке
,
то ряд называется сходящимся
в точке
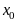 ,
а сама точка
,
а сама точка
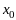 называется точкой
сходимости ряда.
Множество значений
,
при которых ряд (7.1) сходится, называется
областью
сходимости функционального ряда.
называется точкой
сходимости ряда.
Множество значений
,
при которых ряд (7.1) сходится, называется
областью
сходимости функционального ряда.
Область
сходимости функционального ряда
обозначим
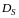 .
Как правило, область
.
Как правило, область
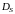 не совпадает с областью
не совпадает с областью
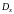 ,
а является ее подмножеством, т.е.
,
а является ее подмножеством, т.е.
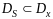 .
.
33. Степенной ряд. Интервал и радиус сходимости степенного ряда.
Степенным рядом называется функциональный ряд вида
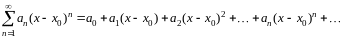
, (3.2)
где
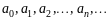
постоянные числа, называемые коэффициентами
ряда,
фиксированное число.
постоянные числа, называемые коэффициентами
ряда,
фиксированное число.
При
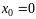 получаем степенной ряд вида
получаем степенной ряд вида
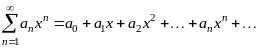 . (3.3)
. (3.3)
Ряд
(3.2) легко приводится к ряду (3.3), если
положить
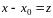 .
Поэтому при изучении степенных рядов
иногда ограничиваются степенным рядом
(3.3).
.
Поэтому при изучении степенных рядов
иногда ограничиваются степенным рядом
(3.3).
Выясним
вопрос о сходимости степенного ряда
(3.3). Область сходимости этого степенного
ряда содержит, по крайней мере, одну
точку
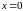 (ряд (3.2) сходится в точке
(ряд (3.2) сходится в точке
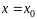 ).
).
Об области сходимости степенного ряда можно судить, исходя из следующей теоремы.
Теорема
3.1 (теорема Абеля).
Если степенной ряд (3.3) сходится в точке
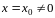 ,
то он абсолютно сходится при всех
,
удовлетворяющих неравенству
,
то он абсолютно сходится при всех
,
удовлетворяющих неравенству
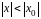 .
.
Пусть
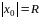 .
Интервал
.
Интервал
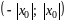 или
или
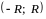 называют интервалом
сходимости.
Число
называют интервалом
сходимости.
Число
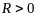 называют радиусом
сходимости
степенного ряда. Таким образом,
называют радиусом
сходимости
степенного ряда. Таким образом,
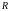
это такое число, что при всех
это такое число, что при всех
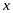 ,
для которых
,
для которых
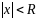 ,
ряд (3.3) абсолютно сходится, а при
,
ряд (3.3) абсолютно сходится, а при
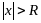 ряд расходится (см. рисунок).
ряд расходится (см. рисунок).

