
- •2. Геометрический и физический смысл двойного интеграла. Основные свойства двойного интеграла.
- •4. Вычисление двойного интеграла в полярных координатах.
- •6. Тройной интеграл. Схема получения тройного интеграла.
- •1) Разбиваем область на «элементарных областей» .
- •3) Возьмем произвольную точку .
- •5) Составляем интегральную сумму
- •7. Основные свойства тройного интеграла (хотя бы 4 свойства). Формула вычисления тройного интеграла в декартовой системе координат.
- •3. Если область разбить линией на две области и такие, что , а пересечение , где линия, разделяющая и (см. Рисунок), то
- •8. Замена переменной в тройном интеграле. Вычисление тройного интеграла в цилиндрических координатах.
- •9. Замена переменной в тройном интеграле. Вычисление тройного интеграла в сферических координатах.
- •10. Некоторые приложения тройного интеграла в геометрии и физике.
- •11. Криволинейный интеграл I рода. Основные свойства кри-I.
- •12. Вычисление криволинейного интеграла I рода: явное представление кривой, параметрическое представление кривой, полярное представление кривой.
- •13. Некоторые приложения кри-I рода в геометрии и физике.
- •14. Криволинейный интеграл II рода. Основные свойства кри-II.
- •15. Вычисление кри-II: явное представление кривой, параметрическое представ-ление кривой. Некоторые приложения кри-II.
- •16. Формула Остроградского – Грина
- •17. Поверхностный интеграл I рода. Основные свойства поверхностного интеграла I рода. Вычисление поверхностного интеграла I рода.
- •3.2. Вычисление поверхностного интеграла I рода
- •18. Поверхностный интеграл II рода. Свойства поверхностного интеграла II рода.
- •19. Вычисление поверхностного интеграла II рода. Формула Остроградского - Гаусса для вычисления поверхностного интеграла II рода.
- •20. Скалярное поле. Производная по направлению. Градиент.
- •21. Векторное поле. Векторные (силовые) линии. Векторная трубка.
- •22. Поток векторного поля через поверхность. Формула вычисления потока векторного поля. Источник и сток. Формула Остроградского – Гаусса для вычисления потока.
- •23. Дивергенция поля. Ротор поля. Формула Стокса.
- •24. Циркуляция поля. Физический смысл циркуляции поля. Формула Стокса.
- •25. Векторные дифференциальные операции первого порядка. Оператор Гамильтона. Перечислить векторные дифференциальные операции второго порядка.
- •26. Классификация векторных полей: определения соленоидального, потенциального и гармонического векторного поля.
- •27. Числовой ряд. N-ая частичная сумма ряда. Сходимость и расходимость ряда. Некоторые свойства рядов. -ый остаток ряда.
- •28. Сформулировать и доказать необходимый признак сходимости ряда. Достаточ-ный признак расходимости ряда. Гармонический ряд.
- •29. Признаки сравнения рядов. Признак Даламбера.
- •30. Радикальный признак Коши. Интегральный признак Коши. Ряд Дирихле.
- •31. Знакочередующиеся ряды. Признак Лейбница. Абсолютная и условная сходимости рядов.
- •32. Функциональный ряд. Точка сходимости. Область сходимости функционального ряда. -ая частична сумма и -ый остаток функционального ряда.
- •33. Степенной ряд. Интервал и радиус сходимости степенного ряда.
- •34. Ряды Тейлора и Маклорена. Разложение функций в степенной ряд.
- •38. Теорема Дирихле. Разложение в ряд Фурье четных и нечетных функций.
- •39. Теорема Дирихле. Разложение в ряд Фурье функций произвольного периода.
27. Числовой ряд. N-ая частичная сумма ряда. Сходимость и расходимость ряда. Некоторые свойства рядов. -ый остаток ряда.
Числовым рядом (или просто рядом) называется выражение вида
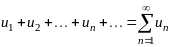 ,
(1.1)
,
(1.1)
где
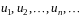
члены ряда
(действительные или комплексные числа),
число
члены ряда
(действительные или комплексные числа),
число
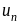
общий член
ряда.
общий член
ряда.
Ряд
считается заданным, если известно
правило, по которому для любого номера
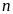 можно записать соответствующий член
ряда:
можно записать соответствующий член
ряда:
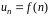 ,
т.е. при помощи формулы
,
т.е. при помощи формулы
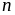 -го
члена.
-го
члена.
Если
формула
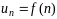 дана, то можно сразу написать любой член
ряда. Например, если
дана, то можно сразу написать любой член
ряда. Например, если
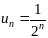 ,
то ряд имеет вид:
,
то ряд имеет вид:
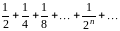 .
Если
.
Если
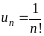 (
(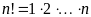 ),
то ряд имеет вид:
),
то ряд имеет вид:
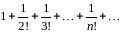 .
.
Иногда
ряд задается при помощи рекуррентного
соотношения,
связывающего последующий член ряда с
предыдущим. При этом задается несколько
первых членов ряда и формула, по которой
находятся следующие члены ряда. Например,
пусть
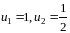 ,
а рекуррентная формула такова:
,
а рекуррентная формула такова:
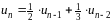 .
Последовательно находим
.
Последовательно находим
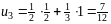 ;
;
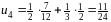 и т.д. Таким образом, получаем ряд:
и т.д. Таким образом, получаем ряд:
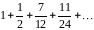 .
.
Определение
1.2. Сумма
конечного числа
 первых членов ряда называется
первых членов ряда называется
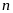 -й
частичной суммой ряда:
-й
частичной суммой ряда:
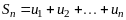 .
.
Рассмотрим частичные суммы
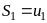 ,
,
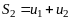 ,
,
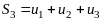
………………….
Если
существует конечный предел
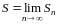 ,
то этот предел называют суммой
ряда (1.1)
и говорят, что ряд сходится.
Если
,
то этот предел называют суммой
ряда (1.1)
и говорят, что ряд сходится.
Если
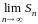 не существует или
не существует или
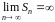 ,
то ряд (1.1) расходится
и суммы не имеет. Например, ряд
,
то ряд (1.1) расходится
и суммы не имеет. Например, ряд
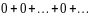 сходится и его сумма равна 0; ряд
сходится и его сумма равна 0; ряд
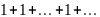 расходится, так как
расходится, так как
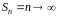 при
;
ряд
при
;
ряд
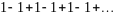 расходится, так как последовательность
частичных сумм не имеет предела.
расходится, так как последовательность
частичных сумм не имеет предела.
28. Сформулировать и доказать необходимый признак сходимости ряда. Достаточ-ный признак расходимости ряда. Гармонический ряд.
Нахождение
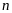 -й
частичной суммы
-й
частичной суммы
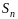 и ее предела для произвольного ряда во
многих случаях является непростой
задачей. Поэтому для выяснения сходимости
ряда устанавливают специальные признаки
сходимости.
Первым из них, как правило, является
необходимый признак сходимости.
и ее предела для произвольного ряда во
многих случаях является непростой
задачей. Поэтому для выяснения сходимости
ряда устанавливают специальные признаки
сходимости.
Первым из них, как правило, является
необходимый признак сходимости.
Теорема
1.1. (необходимый признак сходимости
ряда) Если
ряд (1.1) сходится, то его общий член
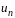 стремится к нулю, т.е.
стремится к нулю, т.е.
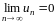 .
.
Доказательство.
Пусть ряд (1.1) сходится и
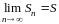 .
Тогда
.
Тогда
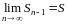 (при
(при
 и
и
 ).
Учитывая, что
).
Учитывая, что
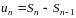 при
при
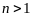 ,
получаем:
,
получаем:
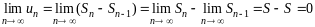 .
.
Теорема
1.2. (достаточный признак расходимости
ряда) Если
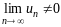 или этот предел не существует, то ряд
расходится.
или этот предел не существует, то ряд
расходится.
Теорему 1.2. примем без доказательства.
Теорема
1.1 дает необходимое условие сходимости
ряда, но не достаточное: из условия
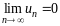 не следует, что ряд сходится. Это означает,
что существуют расходящиеся ряды, для
которых
не следует, что ряд сходится. Это означает,
что существуют расходящиеся ряды, для
которых
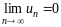 .
.
Например, гармонический ряд
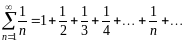 (1.7)
(1.7)
общий член стремится к нулю, однако ряд расходится.
29. Признаки сравнения рядов. Признак Даламбера.
Сходимость или расходимость числовых рядов с положительными членами часто устанавливается путем сравнения его с другим («эталонным») рядом, о котором известно, сходится он или нет. В основе такого сравнения лежат следующие теоремы, которые примем без доказательства.
Теорема 1.3. Пусть даны два ряда с положительными членами:
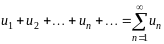 (1.8)
(1.8)
и
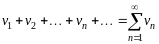 (1.9)
(1.9)
Если
для всех
выполняется неравенство
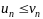 ,
то
,
то
из сходимости ряда (1.9) следует сходимость ряда (1.8);
из расходимости ряда (1.8) следует расходимость ряда (1.9).
Надо
отметить, что теорема 1.3 справедлива и
в том случае, когда неравенство
выполняется не для всех членов рядов
(1.8) и (1.9), а начиная с некоторого номера
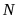 .
Это вытекает из свойства 3 числовых
рядов.
.
Это вытекает из свойства 3 числовых
рядов.
Теорема 1.4 (предельный признак сравнения). Пусть даны два ряда (1.8) и (1.9) с положительными членами. Если существует конечный, отличный от нуля, предел
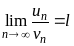
где
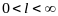 ,
то ряды (1.8) и (1.9) сходятся или расходятся
одновременно.
,
то ряды (1.8) и (1.9) сходятся или расходятся
одновременно.
Признак Даламбера
В отличие от признаков сравнения, где все зависит от догадки и запаса известных сходящихся и расходящихся рядов, признак Даламбера (1717 – 1783, французский математик) позволяет часто решать вопрос о сходимости ряда, проделав лишь некоторые операции над самими рядами.
Теорема 1.5 (признак Даламбера). Пусть дан ряд (1.1) с положительными членами и существует конечный или бесконечный предел
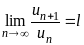 .
.
Тогда:
при
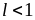 ряд сходится;
ряд сходится;при
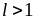 ряд расходится.
ряд расходится.
При
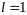 признак Даламбера не дает ответа на
вопрос о сходимости или расходимости
ряда. В этом случае сходимость ряда
исследуется с помощью других признаков.
признак Даламбера не дает ответа на
вопрос о сходимости или расходимости
ряда. В этом случае сходимость ряда
исследуется с помощью других признаков.
Признак
Даламбера целесообразно применять,
когда общий член ряда содержит выражения
вида
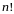 или
или
 .
.
