Вопрос №1.

Фигура и модели Земли

Речь идет о воображаемом земном теле, которое можно представить поверхностью уровня вод Мирового океана, про¬долженной под всеми материками. Такая поверхность называется уровенной, и важным ее свойством является то, что в любой точке она перпендикулярна вектору силы тяжести g.

Фигура, образованная уровенной поверхностью, имеющая неправильную геометрическую форму называется геоидом.

Для решения задач мор¬ской навигации используют аппрок¬симацию (приближение) геоида те¬лом правильной математической формы. Это тело-эллипсоид вращения, полученный в результате вращения эллипса вокруг малой оси.

Используют следующие условия аппроксимации:

- объем эллипсоида предполагается равным объему геоида;

- большая полуось эллипсоида а совпадает с плоскостью эквато¬ра геоида;

- малая полуось b направлена по оси вращения Земли;

- сумма квадратов уклонений поверхности эллипсоида от поверхности геоида выбирается минимальной.

Такой эллипсоид получил название общеземного эллипсоида. Общий земной эллипсоид имеет малое сжатие и практически совпа¬дает со сфероидом — фигурой равновесия вращающейся жидкой массы. Их расхождение по высоте поверхностей составляет всего 2...3 м, поэтому эти два тела часто отождествляют. Понятие «земной сфероид» аналогично понятию «земной эллипсоид».

Для геодезических и картографических расчетов в определенных районах Земли необходимо иметь земной эллипсоид, поверхность ко¬торого максимально совпадает с поверхностью этого района. Очевид¬но, что такой эллипсоид должен иметь вполне определенные ориен¬тацию и размеры. Это референц-эллипсоид.

В России в качестве референц-эллипсоида принят референц-эллипсоид Ф.Н. Красовского. Он имеет следующие параметры:

В навигационных задачах, не требующих высокой точности, Зем¬лю принимают за шар, объем которого равен объему земного эллип¬соида, исходя из соотношения

Для референц-эллипсоида Ф. Н. Красовского радиус модели Зем¬ли как шара равен R = 6 371 110 м.

В ряде стран Западной Европы используют референц-эллип¬соид Хайфорда; в Японии, Германии, Швеции, Греции — Бессе¬ля; в странах Центральной и Северной Америки — Кларка; в Ве¬ликобритании и Ирландии — референц-эллипсоид Эйри.

Для определения места судна с помощью глобальных рнс, применяются референц-эллипсоиды, имеющие международный статус. С их помощью согласуются измере¬ния, произведенные в различных странах. Это общеземные, или между¬народные, референц-эллипсоиды, оптимальные по критерию минимума отклонения от поверхности геоида в целом. В качестве модели геоида для спутниковых навигационных систем в настоящее время применяется модель WGS-84 (World Geodetic System - 1984).

Системы координат

Для определения положения точки на поверхности земного сфе¬роида применяют так называемую географическую систему коорди¬нат. В этой системе координатными линиями являются параллели и меридианы. Любую точку определяют пересечением соответствующих координатных линий, а в качестве начала системы используют пересечение экватора и нулевого меридиана.

Земная ось «протыкает» сфероид в двух точках, называемых гео¬графическими полюсами, северным и южный Географические полюса еще называют истинными.

параллелями (pl).

большой круг, это экватор (EQ).

Следы - географическими или истинными меридианами.

Меридиан, проходящий через точку наблюдения, — истинный меридиан наблюдателя.

Географической широтой φ некоторой точки на поверхности земного сфероида называется угол между плоскостью экватора и нормалью к этой поверхности.

Применение нормали, или отвес¬ной линии, для определения ши¬роты говорит о том, что в ее основу заложены не только геометриче¬ские, но и физические принципы. Широта измеряется дугой мери¬диана от экватора до параллели данной точки (рис. 1.4).

Совершенно очевидно, что на параллелях φ = const.

В некоторых прикладных дисциплинах, смежных с навигацией, используется понятие геоцентрической широты φ'. Как вид¬но из рис. 1.4, геоцентрическая широта φ' < φ. Величина их разности r называется редукцией широты и вычисляется по следующей формуле в угловых единицах:

где а — полярное сжатие; φ — географическая широта.

Географической долготой λ некоторой точки на поверхности сфероида называется двугранный угол между плоскостью началь¬ного (нулевого) меридиана и плоскостью меридиана данной точки.

Долгота измеряется наименьшей дугой эква¬тора.

Разность широт и разность долгот

Перемещение точки в любой координатной системе определя¬ется приращением координат. Осуществляя движение по поверх¬ности Мирового океана, судно использует в основном географиче¬скую систему для фиксации своего положения, поэтому прираще¬ния координат — это приращения широты и долготы. В морской навигации приняты термины разность широт и разность долгот.

Разностью широт (РШ, ∆φ) называют дугу меридиана, заключен¬ную между параллелями φ1 — точки отшествия (отхода) и φ2 — точки пришествия (прихода).

пределах от 0 до 180°

Разностью долгот (РД, ∆λ) называют наименьшую из дуг экватора, заключенную между меридианами точки отшествия λ1 и точки пришествия λ2.

П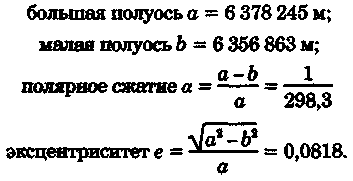 ределы от 0 до 180

Вопрос №2.

Основные понятия картографии:

В математической картографии под развертыванием одной поверхности на другую понимают такое преобразование первой поверхности изгибанием, при котором сохраняются все элементы ее внутренней геометрии, а именно углы, площади, Гауссова кривизна, а также свойство кратчайших линий оставаться кратчайшими-ортодромичность.

Гауссова кривизна - в любой точке каждой поверхности существуют два взаимно перпендикулярных нормальных сечения, имеющих наибольший и наименьший радиусы кривизны по сравнению с другими нормальными сечениями Они называются главными радиусами кривизны в данной точке поверхности. Гауссова кривизна k, являющаяся мерой кривизны поверхности в данной точке, K=1/(R1R2) (41) где R1 и R2 — главные радиусы кривизны

Одну поверхность можно развернуть на другую в том и только в том случае, если они имеют одинаковую Гауссову кривизну.

Картой называется уменьшенное, обобщенное изображение земной поверхности на плоскости, полученное по определенному математическому закону. Этот математический закон называется картографической проекцией.

В общем виде это можно записать так: x=f1(φ,λ) y=f2(φ,λ) (44) где x и y — координаты изображения точки в системе картографических прямоугольных координат xоу, f1 и f2 — математические функции, необходимые для связи между этими системами координат, x и y —координаты точки на земной поверхности.

При выборе функций - два ограничения, которые должны действовать по крайней мере в части карты, предназначенной для практического пользования. 1-точка М0 на земной поверхности должна изображаться только одной точкой М на плоскости проекции. 2-изображение должно быть непрерывным

Планом называется такое изображение земной поверхности на плоскости, в котором искажения не выходят за пределы графической точности.

За меру графической точности можно принять 0,2 мм, что соответствует диаметру следа от укола циркулем. Для планов характерны постоянство масштабов и отсутствие искажений углов.

Масштабы планов и карт

Масштабом плана μ называется отношение любой длины отрезка L на плане к соответствующей длине отрезка Lо на земной поверхности: μ =L/Lо. – это численный масштаб плана. (μ =1/C) (С = L/Lо)

графические масштабы-шкала или диаграмма-циркулем-измерителем расстояние, соответствующее на плане заданному числу единиц на земной поверхности- линейными

масштаба карты во всех точках и по всем направлениям масштаб плана одно и то же значение.

Предельной точностью масштаба называется длина линии на местности, соответствующая длине отрезка на плане, равной 0,2 мм.

Частным, масштабом проекции или карты μ в данной точке по данному направлению называется отношение бесконечно малого отрезка dL в проекции к соответствующему отрезку dL0 на изображаемой поверхности: μ =1/C (с=dl0/dl)

В силу неизбежных искажений на карте частный масштаб изменяется при переходе от одной точки к другой и при переходе от одного направления к другому.

На картах есть масштаб μo- главный масштаб карты. Он представляет собой некоторый средний масштаб в пределах карты, соблюдаемый только в некоторых точках или по некоторым линиям.

Отношение частного масштаба μ, к главному масштабу μо называется увеличением масштаба (с = μ/μо = С0/С = dlds0 / (dl0ds) = dl / (ds)) Оно представляет собой множитель, на который нужно умножить главный масштаб μо, чтобы получить частный масштаб μ. Увеличение масштаба связано с искажением длин ν.

Искажение длин v=с—1=dl/(ds)—1=(dl—ds)/(ds). Его часто выражают в процентах:

v = (с— 1)100% = (Со/С—1)100%.

Классификация картографических проекций

по характеру искажений

В равноугольных проекциях не искажаются углы, сохраняются подобие бесконечно малых фигур,

а = b = с = m = n, т. е. масштаб в данной точке по всем направлениям постоянен. При переходе же от точки к точке масштаб изменяется.

Частный масштаб на картах в равноугольной проекции зависит только от положения, но не от направления измеряемой линии, поэтому можно проводить измерения линий по частям. Морские навигационные карты строят в равноугольной цилиндрической проекции, масштаб которой изменяется только с широтой, оставаясь постоянным на данной параллели.

Проекции, в которых изображения на картах сохраняют постоянство масштабов площадей, называют равновеликими. (окружность на глобусе изобразится на карте эллипсом, но площадь эллипса равна площади круга на сфероиде-будет меняться лишь его форма).

Равнопромежуточные проекции сохраняют постоянный масштаб длин по одному из главных направлений, т. е. а=1 или b=1, где а и b — увеличения масштабов по главным направлениям. Произвольные проекции — это все прочие проекции, не обладающие перечисленными выше свойствами.

по виду нормальной сетки

Коническими называют проекции, в которых меридианы изображаются всегда радиальными прямыми, пересекающимися под углами, пропорциональными разностям долгот, т. е. не равными соответствующим углам в натуре. Можно получить коническую проекцию, описав около глобуса касательный (рис. 4.14) или секущий конус. Частными случаями конических проекций являются азимутальные и цилиндрические проекции.

Азимутальными называют проекции, у которых параллели нормальной сетки — концентрические окружности, а меридианы — радиально расходящиеся из центра этих окружностей прямые линии, пересекающиеся под углами, равными разностям долгот.

Перспективными называются азимутальные проекции, которые получаются путем проецирования точек поверхности шара на картинную плоскость К лучами, исходящими из постоянной точки зрения О. Точка зрения берется на перпендикуляре к картинной плоскости, проходящем через центр шара радиусом R. В зависимости от положения точки зрения и ее расстояния D до картинной плоскости перспективные проекции делятся на:

-центральные, или гномонические (точка O1, D = R)

-стереографические (точка О2, D = 2R)

-внешние (точка 03, 2R< D < ∞)

-ортографические (точка 04, D = ∞).

Цилиндрические проекции— это проекции, на которых параллели нормальной сетки представляют собой прямые, параллельные экватору, а меридианы — прямые, перпендикулярные параллелям и удаленные от изображения начального меридиана на расстоянии у, пропорциональные долготам.

Большинство цилиндрических проекций получается не прямым перспективным проецированием условного глобуса на поверхность цилиндра, а в результате расчета величин х и у по уравнениям проекций, различаются между собой характером функции x = f(φ), определяющей расстояние х параллелей φ от экватора. Это уравнение у = cλ (где с—коэффициент пропорциональности, а λ—долгота)

Вопрос №4.

Погрешности

Вероятность и частота

Никакие измерения, в том числе и навигационные, не могут быть абсолютно точными. Любые измерения неизбежно сопровождаются появлением погрешностей.

Погрешности навигационных измерений, а следовательно, определений места судна и поправок приборов, проявляются как случайные величины, изучение и учет которых требуют применения методов теории вероятностей и математической статистики.

Случайным событием (явлением) называют такое, которое при определенных условиях может либо произойти, либо не произойти, например отказ навигационного прибора в течение данных суток.

Вероятностью (Р) случайного события называют объективную возможность его появления при определенных условиях.

Среди случайных событий выделяют достоверные, которые непременно происходят при определенных условиях. Таким событиям приписывают вероятность Р = 1. Невозможными называют события, которые никак не могут произойти при данных условиях, и для них принимают Р = 0.

Полной группой событий называют такую их совокупность, из которой хотя бы одно непременно происходит, что, однако, не исключает возможности наступления сразу двух или более событий из этой группы.

Несовместными называют события, которые никак не могут произойти одновременно.

Противоположными называют два несовместных события, составляющих полную группу. Равновозможными называют события, вероятность появления которых одинакова.

Для определения вероятностей случайных событий применяют три способа: непосредственный подсчет, по частотам, косвенно через вероятности других событий.

Непосредственный подсчет вероятности возможен, если удается выявить полную группу n несовместных и равновозможных событий, часть из которых m подлежит вероятностной оценке: Р = m/n.

Определение вероятности по частоте - по статистическим данным или по результатам опытов. При этом выявляют число m, когда фактически произошло рассматриваемое событие, и общее число n случаев Частота Р* = m/n.

Косвенное определение вероятностей выполняют путем операций над вероятностями других событий, более доступных для определения.

Для таких расчетов пользуются в общем случае условной вероятностью, например события А при условии, что событие В уже произошло, т. е. Р(А\В) или РА(В). Если условные вероятности равны безусловным, т. е. Р(А\В) = Р(А); Р(В\А)=Р(В),

то такие события независимы.

Теорема умножения вероятностей: вероятность совместного наступления двух событий равна произведению вероятности одного из них на условную вероятность второго при условии, что первое событие произошло. При этом безразлично, какое из двух событий считать первым:

Р(А и В) = Р(А)Р(В\А) = Р(В)Р(А\В).

Теорема сложения вероятностей: вероятность наступления одного из двух событий равна сумме их вероятностей без вероятности совместного наступления этих событий:

Р(А или В) = Р(А) + Р(В)—Р(А и В).

Оценка точности измерений.

Международная морская организации (ИМО) создала стандарт точности судовождения, принятому в 1983 г. на 13-й Ассамблее ИМО в резолюции А.529 (табл. 8.1).

Все ошибки, возникающие при наблюдениях (включая и их обработку), подразделяются на случайные, промахи (грубые ошибки) и систематические ошибки.

Точность измерения навигационного параметра оценивают:

-статистической обработкой серии измерений;

-расчетом средних статистических значений ошибок измерений на основе обобщения опыта плавания (априорно);

-принятием значений ожидаемых ошибок в измерении навигационных параметров по данным технических условий на приборы или системы.

Наиболее простым способом расчета m — средней квадратичной ошибки измерения при равноточных наблюдениях — является способ с использованием коэффициента размаха k.

Систематические ошибки — это ошибки, величина и направления которых постоянны или изменяются по определенному закону.

Систематические ошибки, как правило, должны исключаться введением поправок или специальной организацией наблюдений и их обработкой.

Если на измерения двух навигационных параметров влияют какие-то общие факторы, то ошибки таких измерений оказываются взаимозависимыми. Эта зависимость характеризуется коэффициентом корреляции г. Оценки точности измерений, полученные по результатам тех измерений, для характеристики точности которых они служат, называются апостериорными. Для вывода такой оценки необходима серия из 9... 11 измерений. В практике судовождения такие наблюдения практически невозможны, поэтому здесь широко применяются априорные оценки, полученные на основе обобщения ранее накопленного опыта.

Вопрос №9

АСТРОНОМИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ПОПРАВКИ КОМПАСА

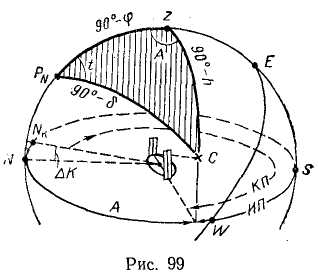
Чтобы определить поправку компаса в мо­ре, необходимо получить истинное направление на светило С, т. е. его ИП (рис. 99), и компасное направление на светило, т. е. его КП, тогда величина и знак ΔК определяются по формуле ΔК = ИП — КП.

И стинный пеленг светила, равный азимуту его в круговом счете, в море вычисляют по формулам, таблицам, номограммам, приборам или ЭВМ. Азимут является функцией трех аргументов, т. е.

А = A₁ (φ, δ, t) = А₂ (φ, δ, h) = А₃ (φ, h, t)

Метод моментов. Если при пеленговании светила замечен момент по хронометру и сняты с карты φ_c , λ_c , то ΔPnC по формуле котангенсов: ctg А — tg δ cos φ_c cosec t_M — sin φ_c ctg t_M.

По этой формуле вычисляют азимут в полукруговом счете, переводят в круговой счет и принимают за ИП.

Метод высот. cos А — sin δ sec φ_c sec h — tg φ_c tg h

Применяется, когда высоту можно вычислить заранее

Метод высот и моментов. Если после наблюдения высот светила взять его пеленг по компасу и заметить Тхр, то одновремен­но с получением места судна или линии положения можно получить и поправку компаса.

Для вычисления h и A применяется система формул:

Вопрос №5.

НФ НП НИ

Для определения обсервованных координат с помощью различных навигационных средств измеряются навигационные параметры (НП).

НП -это линейные или угловые величины , функционально зависящие от координат места судна и координат навигационных ориентиров.

навигационные параметры:

•Дистанция до ориентира (D)

•Пеленг на ориентир (П). Здесь под пеленгом понимается истинный пеленг (ИП), но для упрощения записей в сокращении будем использовать букву П.

•Горизонтальный угол между двумя ориентирами ()

•Вертикальный угол ориентира ()

•Разность расстояний до двух ориентиров (D)

•Высота светила (h)

множество значений НП определяют навигационную функцию (НФ), т.е. зависимость НП от координат места судна

НФ- это математическая зависимость НП от координат места судна

U=f(,)

НИ- это геометрическое место точек равных значений навигационных параметров U₀=f(,)=const

ее вектор-градиент g , который характеризует максимальную скорость изменения навигационной функции

Градиент навигационной функции - это вектор максимальной скорости изменения НФ в конкретной точке поля навигационных параметров, который направлен по нормали к навигационной изолинии в сторону увеличения НП.

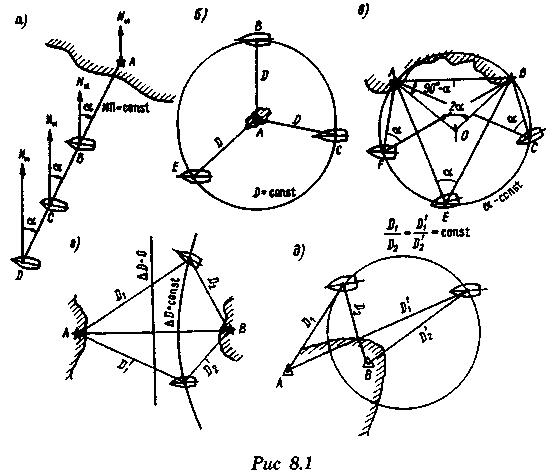
Пеленг. На судне измерен истинный пеленг (ИП) предмета А (рис. 8.1, а), равный α. Проложив на карте линию пеленга AD, можно утверждать, что судно в момент взятия пеленга находилось на этой линии, так как в противном случае значение пеленга было бы отлич­ным от измеренного. Однако неизвестно, в какой точке (В, С, D) на ли­нии пеленга находится судно. Прямая линия AD, отвечающая условию ИП = α, на которой находилось судно в момент наблюдения, будет на­зываться изолинией пеленга или изопеленгой (изоазимутой на сфере).

Расстояние. Измерено расстояние D между судном и ориенти­ром А (рис. 8.1, б). В этом случае судно будет находиться на окружно­сти радиусом D с центром в точке А. Эта окружность будет называть­ся изолинией расстояния или изостадией.

Горизонтальный угол. Если измерен горизонтальный угол меж­ду предметами А и В (рис.8.1, в) равный α, или этот угол вычислен как разность двух пеленгов α = ИП2 – ИП1, то вершина горизонтального угла будет лежать на окружности, проходящей через точки А и B, а центр окружности О будет находиться на перпендикуляре к линии АВ в точке его пересечения с линией, проведенной под углом 90°- α к ли­нии AB (рис. 8.1, в). Эта окружность называется изолинией горизон­тального угла α или изогоной.

Разность расстояний. В некоторых радионавигационных систе­мах измеряется разность расстояний до двух ориентиров. Тогда изоли­нией разности расстояний будет гипербола (рис. 8.1, г).

Линией положения называется прямая, заменяющая участок навигационной изолинии вблизи счислимого места судна.

Градиенты навигационных параметров

Пеленг

Расстояние

Разность расстояний

Горизонтальный угол

Вопрос №6

Прямой аналитический расчет координат места судна

Для омс необходимо измерить ,как минимум, два нп, и зная выражение нф, записать систему уравнений ни.

пример: на судне можем измерить два нп (расстояния) DA и DB до ориентиров A (xA,yA) и B(xB,yB). Имеем систему уравнений навигационных функций:

(1.37)

Теперь необходимо решить систему (1.38) относительно неизвестных координат (x,y) , которые и являются координатами места судна.

Рассмотрим задачу определение места по двум пеленгам на плоскости.

Система уравнений с рис. 1.17 будет иметь вид:

(1.39)

где х₁ ,х₂, y₁, y₂ – координаты навигационных ориентиров.

Обозначив tgП₁ через Т₁,а tgП₂ через Т₁ ,х₀ =х, y₀ =y, запишем алгоритм решения системы:

1. Т₁(х₁–х₀)-y₁ = Т₂(х₁–х₀)–y₂;

2. х₀=(Т₂х₂-Т₁х₁+y₁–y₂)/(Т₂-Т₁);

3. y₀=(Т₁Т₂(х₂-х₁)+Т₂y₁–Т₁y₁)/(Т₂-Т₁);

4. пусть П₁=30, П₂=82, тогда обсервованные прямоугольные координаты рассчитаем так:

5. х₀=(tg(82)*3-tg(30)*8+5-9)/(tg(82)-tg(30)=1.95 мили

6. y₀=(tg(30)*tg(82)*(3-8)+(tg(82) *5-(tg(30)*9)/(tg(82)-tg(30)=1.50 мили.

Аналитический вариант расчета координат места судна по двум линиям положения

Для определения места судна достаточно измерение двух навигационных параметров, так как поверхность на которой ищутся обсервованные координаты двухмерная (положение точки определяется двумя координатами).

Алгоритм расчета таков:

a.В момент времени t измеряются два навигационных параметра Uо1 и Uо2.

b.На этот же момент времени снимаются счислимые координаты xс,yс и на них рассчитываются счислимые навигационные параметры Uс1 и Uс2.

c. На счислимые координаты рассчитываются коэффициенты линий положения aij , т.е. частные производные по навигационным параметрам от навигационных функций.

d.Правые части уравнений линий положения рассчитываются так: U1= Uо1 - Uc1, U2= Uо2 - Uc2.

e.Затем составляется система двух уравнений линий положения, которая может быть переписана в матричном виде, показанном ниже. Соответствующие матрицы имеют следующие названия: A- матрица коэффициентов линий положения, X- вектор неизвестных, U- вектор измерений (вектор свободных членов)

(2.6)

f. Решение системы уравнений линий положения (2.6)

g. Если обозначить вектор счислимых координат, как X_c, а вектор обсервованных координат, как X_о , то можем записать:

представляют собой общие уравнения цилиндрических проекций.

Произвольные-проекции, не вошедшие ни в один из перечисленных классов. Часто их относят к разным классам: -круговые -псевдоконические -псевдоцилиндрические -поликонические и др.

Конические, азимутальные и цилиндрические проекции по характеру искажений могут быть равноугольными, равновеликими и равнопромежуточными.

Морские навигационные карты должны удовлетворять двум

основным требованиям:

-углы, пеленги, курсы, азимуты не должны на них искажаться, т. е. карта должна быть равноугольной;

-линия пути судна должна изображаться прямой, пересекающей меридианы под постоянным углом.

Классификация морских карт

1. Навигационные, ведения счисления пути и определения места судна в море. (общенавигационные, радионавигационные, навигационно-промысловые и навигационно-тактические, карты внутренних водных путей.)

2.Специальные, решения задач судовождения при использовании особых технических средств (рулонные и маршрутные карты, бланковые, обзорные, геофизические )

3.Вспомогательные и справочные (карты-сетки, карты в гномонической проекции для прокладки дуги большого круга, радиомаяков и радиостанций, часовых поясов, сборные листы, батиметрические, шлюпочные, грунтов, рекомендованных путей)

Выбор масштаба карты зависит от расстояния до берега или навигационных опасностей. При плавании вблизи берегов надо подбирать те карты, на которых изображение района наиболее подробное. В зависимости от масштаба общенавигационные морские карты подразделяются на:

-генеральные, имеющие масштаб от 1:1 000 000 до 1:5 000 000;

-путевые, имеющие масштаб от 1:100 000;

-частные в масштабе 1:25 000 до 1:100 000;

-планы, имеющие масштаб от 1:1000 до 1:25 000.

На планы наносят все, что имеет хоть какое-либо отношение к мореплаванию, начиная с навигационной обстановки и кончая различными портовыми сооружениями.

Частные карты содержат все навигационные подробности.

На путевых картах небольшие прибрежные опасности обобщаются, невидимые с моря огни и знаки, как правило, не наносятся, плавучие ограждения, за исключением тех, которые выставлены для ограждения навигационных опасностей, могут быть нанесены не полностью.

На генеральных картах указываются лишь важнейшие маяки и знаки, прибрежные районы имеют только обобщенную характеристику. Комплект судовых карт определяется районом плавания.

Чтобы карты не устаревали, еженедельно издаются Извещения мореплавателям (ИМ) ГУНиО, по радио-для этих целей-НАВАРЕА. Морская акватория -16 районов, назначены страны-координаторы, которые собирают и передают по радио важные навигационные извещения. На судах-«Навтекс». По этим извещениям ведется регулярная корректура карт в соответствии со специальными правилами.

применяется, если высота светила получена предва­рительно, а азимут вычисляется попутно.

Метод высот и моментов применяется также при определениях ΔК по Полярной звезде, но ее высота не измеряется, а принимается равной φ.

ОПРЕДЕЛЕНИЕ ПОПРАВКИ КОМПАСА. ОБЩИЙ СЛУЧАЙ

При видимости светил поправка компаса может быть определена в лю­бое время суток по методу моментов, который и представляет общий случай определения поправки компаса

Предварительные операции. Выбор условий наблюдений. На намеченное время подобрать све­тило с высотой до 10° (и не более 20°) с помощью звездного глобуса или на глаз. Проверка инструментов, Наблюдения. Пронаблюдать серию из трех пеленгов и КП. Получить навигационную информацию: Тс, ол, φ , λ, КК, ΔК.

Обработка наблюдений. Проанализировать ΔК; срав­нить с принятой постоянной - расхождения не должны превышать точности курсоуказания (от ±0,3° в хороших условиях, до 1,5° — в пло­хих);

+ ВАС—58. ТВА—57. ЭВМ.

Вычисление азимута светила и поправки компаса по формуле ctg A.

ПО ВОСХОДУ (ЗАХОДУ) СОЛНЦА

Порядок работы при определении ΔК по восходу (заходу) Солнца.

1. Про­наблюдать пеленг Солнца в момент появления (или погружения) на гори­зонте его верхнего края.

2. Заметить момент Тс до 5м, рассчитать Тгр и выбрать из МАЕ δ до 0,1⁰- На этот же момент снять φ_c до 0,1°, а в высоких широтах — до 3'.

3. Войти в табл. 20-а при одноименных φ и λ или 20-6 при разноимен­ных и выбрать ближайшее к φ и λ значение Ат. Проинтерполировать ази­мут по б и ф и придать поправки к А г. Полученному азимуту приписать наи­менование в полукруговом счете и перевести его в круговой счет.

4. Рассчитать ΔК = ИП — КП.

5. Проанализировать ΔК. сравнением с принятой ранее и оценить воз­можные ошибки определения АК-

Определение поправки компаса по наблюдениям Полярной звезды.

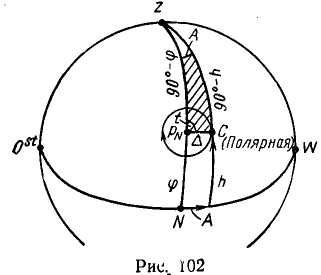
Пример 73. 5 мая 1977 г. в Южно-Китайском море, следуя КК = 190° (+1°), V = 17 уз, определить АГК' по Полярной.

Решение. 1. Наблюдения. Около Т_в = 2^Ч 13^м (№ = —9) пеленговали Полярную-ГКП = 359,6°; ф = 18° N; X = 116° 0^s'.

2. Обработка наблюдений:

Вопрос №10.

Дальность видимого горизонта. Дальность видимости предмета...

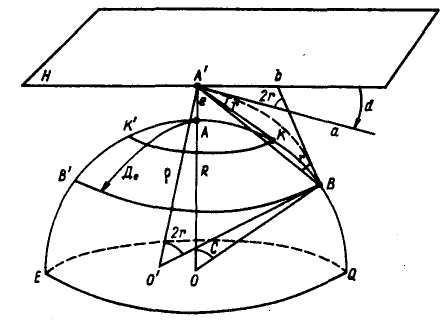
Географическая дальность видимости горизонта

Лучи зрения, идущие к А' и касательные к поверхности воды по всем направлениям, образуют малый круг КК', который называется линией теоретически видимого горизонта.

Луч света распространяется не прямолинейно, а по некоторой кривой А'В, ко­торая может быть аппроксимирована окружностью радиусом ρ. Явление искривления зрительного луча в атмосфере Земли назы­вается земной рефракцией - наблюдатель видит не КК', а линию BB' - Это видимый горизонт наблюдателя.

Коэффициент земной рефракции:

Угол рефракции r .

Сферический радиус А'В называется географической или гео­метрической дальностью видимого горизонта Де. Эта дальность видимости не учитывает прозрачность атмосферы, т. е. считается, что атмосфера идеальна с коэффициентом прозрачности т = 1.

Проведем через точку А' плоскость истинного горизонта Н, тогда вертикальный угол d между Н и касательной к зрительному лучу А'В будет называться наклонением горизонта