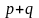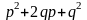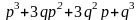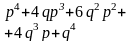Стандартные полиномы для эталонных моделей
При синтезе регулятора состояния требуемое качество управления задают эталонной моделью. Наиболее удобно такую модель описать в канонической форме управляемости (п.2.6)
(п.3.1)
или
.
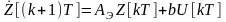(п.3.2)
Матрица АЭ, задающая динамику синтезируемой системы с регулятором состояния, определяется, в свою очередь, через эталонное характеристическое уравнение
.
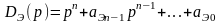(п.3.3)
Выражение (п.3.3) полностью определяет матрицу эталонной модели (п.2.6).
Для непрерывных систем в качестве эталонных характеристических уравнений используют стандартные полиномы: биномиальные, Баттерворта и минимизирующие квадратичную ошибку.
Биномиальный полином задает характеристическое уравнение, у которого все корни (полюса) действительные, отрицательные (необходимое условие устойчивости) и равны между собой
,
(п.3.4)
где
.
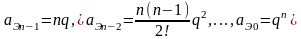В этом случае переходные процессы будут апериодическими, а длительность процесса будет определяться величиной корней q. Чем больше это значение, тем меньше будет длительность переходного процесса. Ниже приведены показатели переходных процессов в зависимости от порядка модели
Таблица п.1
n |
|
, % |
tПq |
1 |
|
0 |
3 |
2 |
|
0 |
4,8 |
3 |
|
0 |
6 |
4 |
|
0 |
7,8 |
Таким образом, величину корней можно определить из заданной длительности переходного процесса. Например, для объекта третьего порядка (n=3)
.
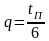Характеристическое уравнение, задаваемое стандартным фильтром Баттерворта, имеет корни, расположенные в левой полуплоскости корней на полуокружности радиуса q. При этом они расположены с равным угловым расстоянием /n. В таблице п.2 приведены показатели переходных процессов в зависимости от порядка модели.
Таблица п.2
n |
|
, % |
tПq |
1 |
|
0 |
3 |
2 |
|
5 |
4,5 |
3 |
|
9 |
6,25 |
4 |
|
11 |
7,0 |
Из сравнений таблиц п.1 и п.2 видно, что биномиальный полином определяет более качественные переходные процессы: при практически одинаковой длительности отсутствует перерегулирование. Тем не менее, фильтр Баттерворта обладает замечательным качеством: частотная характеристика в области средних частот имеет значительную крутизну, что делает перспективным его использование при синтезе регуляторов в системах с высоким уровнем зашумленности сигналов обратной связи или возмущающих воздействий.
Для получения эталонной модели при синтезе дискретного регулятора состояния используются зависимости
,
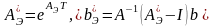где АЭ определяется из требований к качеству переходных процессов в непрерывной форме.