III.1. Представление моделей объектов управления в пространстве состояний

Удобным и единообразным по форме является представление математической модели объекта в виде системы дифференциальных уравнений первого порядка, разрешенных относительно первых производных, т.е. уравнений в форме Коши. Для этого необходимо ввести дополнительные переменные, называемые переменными или координатами состояния объекта. Модель объекта в этом случае будет определяться через функциональную связь трех видов переменных: входных u_i, выходных y_i и внутреннего состояния х_i.

(3.1)

где F_C и F_B – функции состояния и выхода объекта;

U, X, Y – векторные величины, компонентами которых являются переменные u_i, x_i, y_i.

Чтобы лучше разобраться в особенностях описания объекта через переменные состояния, рассмотрим уравнение первого порядка

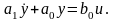(3.2)

Введем обозначение y = x и представим уравнение (3.2) в форме (3.1.)

(3.3)

.

Структурная схема системы (3.3) представлена на рис. 3.1, а.

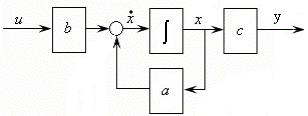
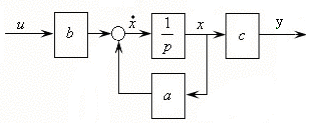
а)непосредственная форма описания б) символьная форма описания

Рис. 3.1.Структурная схема описания объекта регулирования первого

порядка с использованием переменной состояния х

Чаще всего операцию интегрирования всех структурных схем обозначают через оператор 1/р. (см. рис. 3.1, б) Объект, описываемый дифференциальным уравнением n-го порядка, через переменные состояния будет представляться

n- дифференциальными уравнениями первого порядка (в форме Коши)

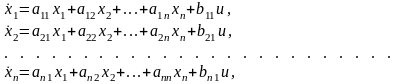(3.4)

где х₁, … х_n – переменные или координаты состояния.

Кроме того, согласно (3.1), требуется уравнение выхода, которое в общем случае будет иметь следующий вид

(3.5)

Уравнения (3.4) и (3.5) справедливы для объекта с одним входом и одним выходом, т.е. когда y, u – скалярные величины. Эти уравнения удобно представить в матричной форме (сводка обозначений и сведения из теории матриц даны в Приложении).

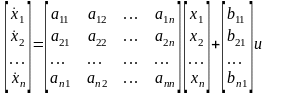(3.6)

,

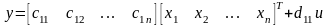где Т – знак транспонирования.

Система (3.6) может быть записана в сжатой форме

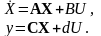(3.7)

где 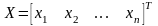- векторная переменная, называемая вектором состояния;

U, y – скалярные переменные;

А – квадратная матрица коэффициентов размерностью n x n;

B – матрица-столбец размерностью n x 1;

С – матрица-строка размерностью 1 х n.

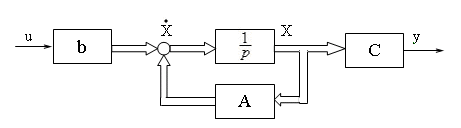
Рис. 3.2. Структурная схема описания n-ого объекта с

использованием вектора состояний Х

Матрица А называется переходной или собственной матрицей объекта, матрицы B и С соответственно – входной и выходной матрицами. Система (3.7) подобна по форме системе (3.3). Соответственно она имеет подобную структурную схему (рис. 3.2). Отличие заключается в замене скалярной величины х вектором Х и заменой коэффициентов матрицами. Широкой стрелкой обозначаются направления действия векторных величин, узкой – скалярных.

для исследования объекта на управляемость, а также для синтеза регуляторов по полному вектору состояния объекта удобно представить модель в так называемой канонической форме управляемости или нормальной форме (см. Приложение 2).

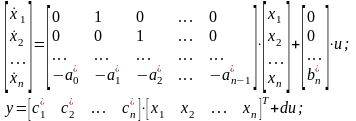(3.18)

На рис. 3.6 представлена структурная схема модели в канонической форме управляемости. Очевидно, что система (3.14) и структура на рис. 3.5 являются представлением объекта второго порядка в нормальной форме. Для электродвигателя определена матрица преобразований модели относительно физических координат в модель нормальной формы. Кроме нормальной формы, широко используются каноническая форма наблюдаемости, диагональная и др.

Для исследования реакции системы на внешние воздействия необходимо решить матричное дифференциальное уравнение (3.7). Рассмотрим первоначальное уравнение первого порядка (3.3). Его решение определяется известным выражением

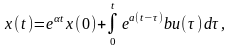(3.24)

где х(0) – начальное значение x(t).

В частном случае при u(t)=const в интервале времени от 0 до t интеграл в (3.24) берется довольно легко

(3.25)

Решение матричного уравнения (3.7) имеет подобный вид [6]

(3.26)

Отличие (3.26) от (3.25) в его многомерности. Поэтому возникает задача определения экспоненциальной функции от матрицы. Для этого можно использовать два подхода. Первый состоит в разложении функции в степенной ряд

. (3.27)

Выражение (3.27) дает приближенное значение функции. Для точного аналитического расчета воспользуемся методом Кэли-Гамильтона. Любую функцию от матрицы можно представить в виде

(3.28)

где n – размерность квадратной матрицы A и коэффициенты а_i определяются из системы уравнений

(3.29)

где i = 1,2,… n; _i – собственные значения матрицы (или корни уравнения (3.23)).

Аналитическое решение уравнения – довольно громоздкая задача. Поэтому чаще используются машинные методы расчета. Для этого выражение (3.27) представим в следующем виде

(3.30)

Такое представление значительно упрощает алгоритм расчета.