Построение переходных процессов по передаточной функции импульсной системы

1 способ

Передаточная функция замкнутой системы

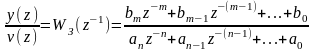, (п. 4.1.)

записываем алгебраическое выражение

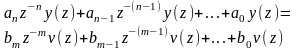. (п. 4.2.)

Подвергая выражение (п. 4.2.) обратному z-преобразованию получим

. (п. 4.3.)

Подставляя в (п. 4.3.) значения тактов квантования k=0,1,2 … получим значения выходной величины в зависимости от задающего сигнала

Пример:

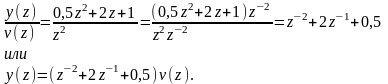
После обратного z-преобразования получим

.

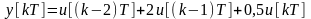В частности, если задающий сигнал постоянный, например единичный сигнал, получим

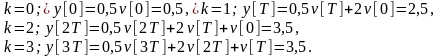
Следовательно, при k=2 (на втором такте) переходный процесс выходит на установившийся режим. График решетчатой функции показан на рис. п. 5.1.

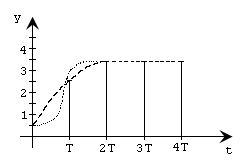
Рис. 4.1. Решетчатая функция переходного процесса y[kT] и возможные варианты непрерывной (реальной) кривой переходного процесса

Вид непрерывных кривых переходных процессов для одной и той же решетчатой функции могут значительно отличаться. Это зависит от динамических свойств объекта управления.

2 способ

Из сравнения выражений дискретной функции

(п.4.4)

и ее z-изображение

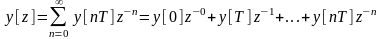. п. 4.5)

видно, что коэффициенты разложения (п.4.5) равны значениям решетчатой функции в соответствующие такты времени. Отсюда следует второй способ нахождения обратного z-преобразования.

Из передаточной функции (п. 4.1) следует, что

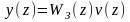
или записав выражение (п. 4.1) и выражение для v(z) относительно положительных степеней z в общем случае получим

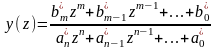. (п. 4.6)

Разложим выражение y(z) в степенной ряд по отрицательным степеням z (в ряд Лорана) путем деления полинома числителя выражения (п. 4.6) на полином знаменателя:

.

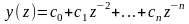В соответствии с выражением (п. 4.5) получим, что

.

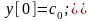Пример

Возьмем ту же передаточную функцию, что и в примере первого способа построения переходных процессов.

Так как задающий (входной) сигнал единичный

v[kT]=1[kT],

то .

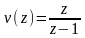Следовательно

.

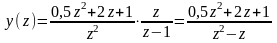Разложим выражение для y(z) в ряд Лорана путем деления полинома числителя на полином знаменателя

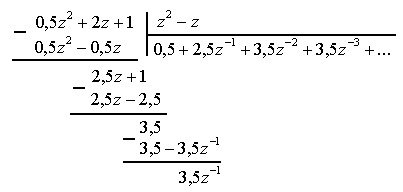
Таким образом

.

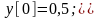Т.е. получили, очевидно, тот же результат что и первым способом.

3 способ заключается в непосредственном применении обратного z-преобразования

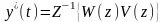. (п. 4.7)

Если в фигурных скобках (п .4.7) стоит сложное выражение, его необходимо разложить на простые слагаемые для использования таблиц прямого и обратного z- преобразования функций.

Из приведенных примеров видно, что построение переходных процессов по импульсной передаточной функции значительно проще, чем для непрерывных функций. Это объясняется тем, что коэффициенты импульсных функций по существу представляют пошаговое решение дифференциальных уравнений, описывающих динамику объекта управления.

II.2. Типовые регуляторы в цифровой реализации

К типовым регуляторам относятся пропорциональные (П), интег­ральные (И), пропорционально-интегральные (ПИ) и пропорционально-интегрально-дифференциальные (ПИД) регуляторы. Цифровой И-регулятор был рассмотрен в качестве примера в §I.1. Этот регулятор является частным случаем ПИД-регулятора. Уравнение непрерывного ПИД-регулятора имеет вид

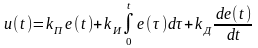. (2.1)

Или применяя преобразование Лапласа, получим

. (2.2)

Такой регулятор наиболее часто применяется на практике. В частнос­ти, система подчиненного регулирования состоит из каскадно вклю­ченных ПИ- и П-регуляторов. Интегральная составляющая обеспечива­ет точность в установившемся режиме, П и Д-составлявшие служат для получения требуемых динамических показателей (длительности пе­реходного процесса, колебательности, величины максимального перерегулирования).

При малых значениях периода Т уравнение (2.1) можно предста­вить в виде разностного

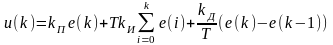. (2.3)

Выражение (2.3) представляет собой не рекуррентный алгоритм управления.

Как было показано ранее, для цифрового управления удобнее реализовать рекуррентный алгоритм. Для его определения найдем

.

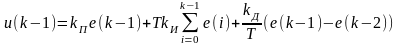Вычитая это уравнение из уравнения (2.3), получим

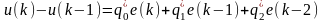, (2.4)

где ; ; .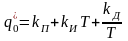

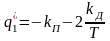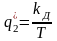Согласно (2.4) Z-преобразованное выражение для дискретно­го ПИД-регулятора будет иметь вид

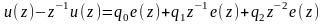. (2.5)

Подчеркнем еще раз, что отличие от (2.4) состоит в том, что коэф­фициенты q₀, q₁, q₂ не зависят от длительности импульсов, т.к. они учитываются в формирующем звене, объединяемом при получении диск­ретной передаточной функции с объектом управления (см. (1.20)).

Согласно (2.5) дискретная передаточная функция регулятора

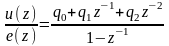. (2.6)

Наличие полюса z = 1 говорит о том, что в установившемся режиме ошибка e(z) будет равна нулю (астатический регулятор).

В общем случае передаточная функция астатического дискретного регулятора имеет следующий вид

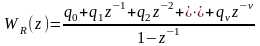. (2.7)

По аналогии с выражением для непрерывного регулятора (2.2) уравнение дискретного регулятора (2.6) можно представить в следующем виде

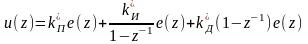. (2.8)

Приравнивая в (2.6) и (2.8) коэффициенты при одинаковых степенях, получим

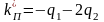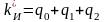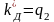; ; . (2.9)

Для расчета оптимальных типовых регуляторов разработаны рекомендации и стандартные соотношения. Поэтому подробно на этом вопросе останавливаться не будем. Другим важным вопросом является выбор периода квантования Т. Максимальное его значение определяется исходя из теоремы Котельникова-Шеннена. Для того чтобы непрерывный сигнал со спектром, ограниченный максимальной частотой _max, можно было восстановить по его дискретной последовательности, необходимо соблюдение условия (см. главу 1)

,

где _Т=2/Т - круговая частота квантования.

При неизвестных значения спектра внешних сигналов выбор периода Т на начальном этапе проектирования можно определить, как показано в § 1.2, из условия

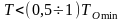, (2.14)

где Т_Omin - минимальная постоянная времени непрерывной передаточной функции объекта.

Условие, при котором поведение дискретной замкнутой системы приближается к непрерывной системе, с достаточной точностью можно определить следующим неравенством

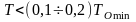. (2.15)

Очевидно, что при соблюдении соотношения (2.15) расчет коэффициентов ПИД-регулятора можно производить по рекомендациям, разработанным для непрерывных систем управления. При переходе к дискретному алгоритму ПИД-регулятора его коэффициенты пересчитываются в соответствии с зависимостями (2.12).

Структурная схема регулятора, соответствующая алгоритму уравнения (2.4) или (2.8), представлена на рис.2.1. С целью ограничения начального броска управляющего воздействия с выхода регулятора при резком изменении задающего сигнала u_з(z), чаще применяют модифицированный алгоритм, структурная схема которого представлена на рис. 2.2.

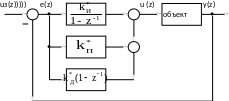
Рис.2.1. Система с дискретным ПИД-регулятором