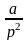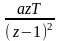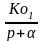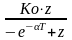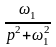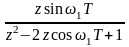- •Глава I Структурно-операторное описание цифровой системы управления
- •I.1. Математическое описание цифровых сау
- •Исследование устойчивости импульсных систем
- •Построение переходных процессов по передаточной функции импульсной системы
- •II.2. Типовые регуляторы в цифровой реализации
- •III.1. Представление моделей объектов управления в пространстве состояний
- •III.3. Дискретное описание систем в пространстве состояний
- •IV.2. Синтез регулятора состояния
- •Стандартные полиномы для эталонных моделей
- •Действия с матрицами
- •Канонические формы моделей описания объекта управления
Глава I Структурно-операторное описание цифровой системы управления
I.1. Математическое описание цифровых сау
В системах управления, содержащих ЭВМ или микропроцессорный регулятор, сигналы квантуются по времени и по уровню. На рис.1.1 представлена одноконтурная система с управляющей ЭВМ. Съём сигналов с датчиков (Д) (опрос датчиков) осуществляется, как правило, с постоянным периодом Т. На схеме квантователь сигналов по времени изображен в виде ключа.
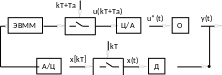
Рис. 1.1. Функциональная схема одноконтурной системы
с управляющей ЭВМ
Если время съёма информации мало, то сигнал с выхода ключа представляет собой значение сигнала x(t) в дискретные моменты времени kT, где k=0,1,2,…( рис.1.2 а, б).
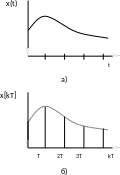
Рис. 1.2. Реальные и идеальные импульсные функции:
а) непрерывная функция х(t); б) импульсная (решетчатая) функция x[kT]
Дискретный сигнал x[kT] в аналого-цифровом преобразователе А/Ц квантуется как по времени, так и по уровню. Управляющие ЭВМ обычно восьми- или шестнадцатиразрядные. В шестнадцатиразрядной сетке последний разряд составляет 0,007% от уровня сигнала. Величина эта ниже величины шумов, поэтому дискретностью по уровню можно пренебречь.
После обработки информации сигналы с ЭВМ снимаются также с периодом Т и с задержкой на время выполнения алгоритма управления ТA. Затем эти сигналы поступают на цифроаналоговый преобразователь Ц/А, с выхода которого снимаются импульсы конечной длительности ТИ (рис.1.3, а). Для простоты изложения сигналы на рис 1.2 и 1.3 совпадают по величине, т.е. передаточные функции алгоритма ЭВМ и Ц/А приняты равными единице. Поэтому сигналу u*(t) (рис.1.1) соответствует сигнал x*(t) . Как правило, длительность ТИ равна периоду квантования, т.е. ТИ=Т.
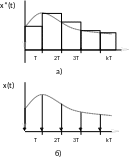
Рис. 1.3. Последовательность идеальных -импульсов
Таким образом, если не учитывать квантования по уровню, управляющая ЭВМ обрабатывает и выдает импульсные сигналы. Поэтому при описании управляющего алгоритма теряется смысл производной и интеграла, так как минимальное приращение временного интервала t=T. В этом случае производная по времени
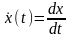
заменяется дискретной функцией
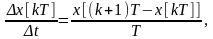 (1.1)
(1.1)
называемой первой разностью. Величина Т=const, поэтому выражение (1.1) часто представляют в относительном времени, т.е. аргументом является число прошедших тактов квантования
 .
.
Аналогично определяются вторая и более высокие разности. Операция интегрирования для импульсных функций заменяется суммированием, а дифференциальные уравнения – разностными. Например, простейшее дифференциальное уравнение первого порядка
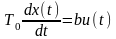
представляется как разностное уравнение первого порядка
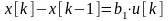 ,
,
где
 .
.
Динамическое звено n-го порядка реализуется алгоритмом работы ЭВМ как разностное уравнение того же порядка. Его удобно представлять, используя оператор сдвига
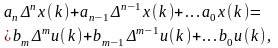 (1.2)
(1.2)
где
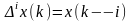 .
.
Чтобы
получить единообразное описание всей
замкнутой системы, необходимо объект
управления представить также дискретной
моделью. Такое представление может быть
осуществлено с помощью преобразования
вида (1.1), но это может привести к
значительным погрешностям. Для получения
точной дискретной модели используется
понятие идеального импульсного элемента
или сигнала. Идеальный импульсный
элемент (сигнал) преобразует непрерывный
сигнал x(t)
в дискретный по времени сигнал
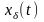 ,
представляющий последовательность
идеальных импульсов, площадь которых
в моменты времени равна значению
функции (сигнала) x(t)
в эти моменты времени (рис.1.3, б).
Аналитическая зависимость между этими
сигналами определяется выражением
,
представляющий последовательность
идеальных импульсов, площадь которых
в моменты времени равна значению
функции (сигнала) x(t)
в эти моменты времени (рис.1.3, б).
Аналитическая зависимость между этими
сигналами определяется выражением

(1.3)
где
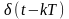 -
идеальный импульс, равный нулю при t
- kT
> 0 и t
- kT
< 0, площадью, равной единице при t
- kT
= 0, то есть в момент времени t
= kT
(дельта – функция). Очевидно, что амплитуда
такого сигнала равна бесконечности.
Поэтому импульсы на рис.1.3, б изображены
в виде стрелок.
-
идеальный импульс, равный нулю при t
- kT
> 0 и t
- kT
< 0, площадью, равной единице при t
- kT
= 0, то есть в момент времени t
= kT
(дельта – функция). Очевидно, что амплитуда
такого сигнала равна бесконечности.
Поэтому импульсы на рис.1.3, б изображены
в виде стрелок.
Так как дискретная функция x[kT] относительно аргумента t является постоянной величиной и равна 0 между моментами kT,
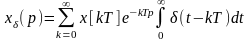
можно записать
 .
(1.4)
.
(1.4)
Преобразование
(1.4) является дискретным эквивалентом
непрерывного преобразования Лапласа.
Для упрощения записи обозначим
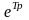 через
z.
В резильтате получим следующее выражение
через
z.
В резильтате получим следующее выражение
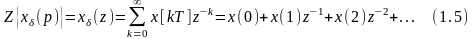
Выражение
(1.5) называется Z-преобразованием.
Этот бесконечный ряд сходится, если
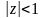 .
.
Для перехода от непрерывной передаточной функции объекта к дискретной передаточной функции, связывающей дискретные входные и выходные сигналы после ключей (квантователей по времени), примем, что эти квантователи (ключи) работают синхронно. Импульсы, поступающие на вход объекта, согласно (1.3) описываются следующим образом:
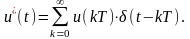
(1.6)
Реакция
на единичный импульс последовательности
(1.6) определятся весовой функцией объекта
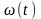 .
Напомним, что весовая функция – это
реакция звена на дельта-функцию.
.
Напомним, что весовая функция – это
реакция звена на дельта-функцию.
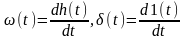 ,
,
где h(t) - реакция этого же звена (объекта) на единичное воздействие 1(t).
Следовательно, сигнал с выхода объекта определяется зависимостью
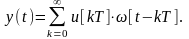
(1.7)
Учитывая, что сигнал y(t) после квантователя передается в ЭВМ в дискретные моменты nT (номер такта n не равен номеру k) ,
из (1.7) получим
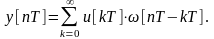
Переходя к переменной z, получим Z-преобразованную передаточную функцию.
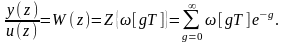
(1.10)
Рассмотрим в качестве примера объект первого порядка
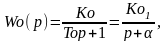
(1.11)
где
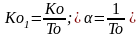 .
.
Весовая функция объекта
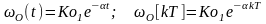 .
.
Подвергнем z-преобразованию это выражение:
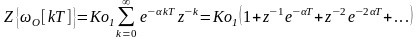 .
.
Этот
ряд представляет собой бесконечно
убывающую геометрическую прогрессию
с коэффициентом
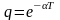 .
Следовательно, сумма этого ряда будет
определяться следующим образом
.
Следовательно, сумма этого ряда будет
определяться следующим образом
 ,
,
где
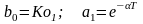 .
.
Преобразование (1.11) для элементарных функций [kT] и x[kT] приводится в таблицах (см., например, табл. 1).
Таблица 1
x(t) |
x(p) |
x[kT] |
x(z) |
(t) |
1 |
[kT] |
1 |
1(t) |
|
1[kT] |
|
|
|
ak2T2 |
|
K0e-T |
|
K0e-kT |
|
sin1t |
|
sin1kT |
|
Если требуется выразить x(z) относительно переменой z в отрицательной степени, переход от табличных выражений, очевидно, элементарно прост. Нужно числитель и знаменатель умножить на z-n , где n – максимальное значение положительного показателя степени при z.
Если передаточная функция W(p) имеет сложный (не табличный) вид, ее необходимо представить в виде элементарных слагаемых, определяемых одним из известных методов. Для каждого слагаемого по таблице находится
Z-преобразованная функция, и исходя из свойства линейности z-преобразования
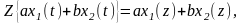 (1.13)
(1.13)
результирующая дискретная передаточная функция W(z) определяется суммированием элементарных слагаемых.
Другим важным свойством Z-преобразования является изображение сдвига по времени на n-тактов влево
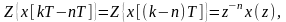
(1.14)
и сдвига на n-тактов вправо (упреждение) при нулевых начальных условиях
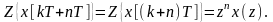
(1.15)
Начальные и конечные значения дискретных функций определяются выражениями

(1.16)
Операция D-преобразования значительно упрощается, если воспользоваться приближенной заменой переменных
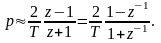
(1.17)
Правомерность такой замены вытекает из разложения в ряд функции z=eTp
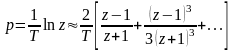 .
.
Преобразования (1.9) и (1.10) справедливы для случая, когда на вход объекта подается последовательность идеальных импульсов нулевой ширины и бесконечно большой амплитуды, площадью, равной u[kT]. Реально на объект действует последовательность импульсов конечной ширины T и конечной амплитуды, равной u[kT] (рис.1.3, а). Поэтому передаточную функцию объекта необходимо дополнить передаточной функцией формирователя WФ(p), преобразующего дискретную функцию u(t) (или x(t) на рис.1.3, б) в дискретную функцию u*(t) (или x*(t) на рис.1.3, а). Связь между этими функциями определяется очевидным выражением
 .
.
Применяя преобразование Лапласа, получим
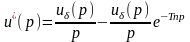
или
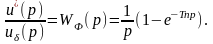
(1.18)
Результирующая передаточная функция непрерывной части
WK(p)=WФ(p)WO(p). (1.19)
На рис.1.4 представлена на основании (1.18) и (1.19) структурная схема непрерывной части системы с идеальным импульсным элементом.

Рис. 1.4. Структурная схема непрерывной части системы
с идеальным импульсным элементом
На рисунке показан общий случай для импульсов шириной Ти. При ширине импульсов, выдаваемых формирующим элементом, равным периоду квантования (Ти = Т), что чаще всего встречается на практике,
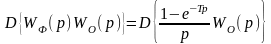 .
.
Используя свойства Z-преобразования, можно доказать, что
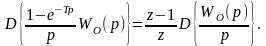
(1.20)
В качестве примера рассмотрим систему, представленную на рис.1.1, с объектом первого порядка (1.11) и управляющей ЭВМ, выполняющей функцию И-регулятора.
Согласно (1.20)
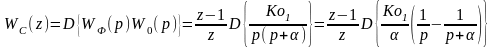 Используя
таблицу 1, получим
Используя
таблицу 1, получим
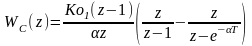 .
.
Окончательно
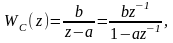
(1.25)
где
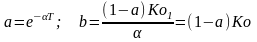 .
.
У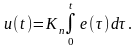 равнение
непрерывного И-регулятора имеет вид
равнение
непрерывного И-регулятора имеет вид
(1.26)
где e(τ) = uЗ(τ) - uOC(τ) - разность между задающим сигналом и сигналом обратной связи (ошибка регулирования). Непрерывная передаточная функция регулятора имеет хорошо знакомый вид
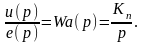
(1.27)
Дискретный И-регулятор описывается уравнением
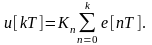
(1.28)
Выражение (1.28) представляет нерекуррентный алгоритм управления. Однако, для программирования ЭВМ удобны рекуррентные алгоритмы. Они основаны на использовании для вычисления управляющего воздействия u[kT] значение этого воздействия на предыдущем шаге расчета

(1.29)
Вычтем из уравнения (1.28) уравнение (1.29)
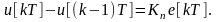
(1.30)
Это уравнение дает рекуррентный алгоритм дискретного И-регулятора

(1.31)
Для получения дискретной передаточной функции подвергнем
Z-преобразованию разностное уравнение (1.30)
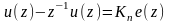 .
.
Следовательно,
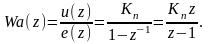
(1.32)
Заметим, что такое же выражение дает непосредственный переход, например, с помощью таблиц или D-преобразования от непрерывной передаточной функции (1.27) к дискретной.
Структурная схема рассматриваемой системы аналогична структуре непрерывной системы (рис.1.5).

Рис. 1.5. Структурная схема одноконтурной
дискретной системы управления
Результирующая передаточная функция этой системы согласно (1.25) и (1.32) имеет вид
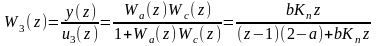
и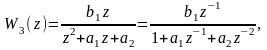 ли
ли
(1.33)
где
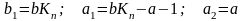 .
.
По этой передаточной функции (1.33) можно исследовать устойчивость замкнутой системы, определить оптимальный коэффициент регулятора KИ и так далее.


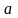 t2
t2