Эконометрика!!!

1. Определение эконометрики. Предмет и методы эконометрики.

Эконометрика - это наука, которая на базе статистических данных дает количественную характеристику взаимозависимым экономическим явлениям и процессам. Слово «эконометрика» произошло от двух  слов:   «экономика» и «метрика» (от греч. «метрон» - «правило определения расстояния между двумя точками в пространстве», «метрия» — «измерение»). Эконометрика - это наука об экономических измерениях.

Основным  предметом исследования эконометрики являются массовые экономические явления и процессы.

Основные эконометрические методы.

1.       сводка и группировка информации;

Статистическая сводка - это научно организованная обработка материалов наблюдения, включающая в себя систематизацию, группировку данных, составление таблиц, подсчет итогов, расчет производных показателей (средних, относительных величин).  Статистическая группировка - это процесс образования однородных групп на основе расчленения статистической совокупности на части или объединения изучаемых единиц в частные совокупности по существенным для них признакам.

2. вариационный и дисперсионный анализ;   

Дисперсия признака - это средний квадрат отклонений вариантов от их средней величины.                                                         В эконометрических расчетах, как правило, используют общую, межгрупповую и внутригрупповую дисперсии. При этом общая дисперсия характеризует вариацию признака в статистической совокупности в результате влияния всех факторов. Межгрупповая дисперсия показывает размер отклонения групповых средних от общей средней, то есть характеризует влияние фактора, положенного в основание группировки. Внутригрупповая (остаточная) дисперсия характеризует вариацию признака в середине каждой группы статистической группировки.                                                                                                                                 

В эконометрических расчетах используется среднее квадратическое отклонение - обобщающая характеристика размеров вариации признака в  совокупности. Оно равно корню квадратному из дисперсии. Для осуществления сравнений колеблемости одного и того же признака в нескольких совокупностях используется относительный показатель вариации — коэффициент вариации.

2.       регрессионный и корреляционный анализ;                                                               

Применение метода наименьших, квадратов (МНК) позволяет получить достаточно точные теоретические значения модели однофакторной регрессии и соответственно ее графическое изображение (термин "регрессия" - движение назад, возвращение в прежнее состояние, - был введен Фрэнсисом Галтоном в конце XIX века при анализе зависимости между ростом родителей и ростом детей; в любом случае средний рост детей - и у низких, и у высоких родителей -стремится (возвращается) к среднему росту людей в данном регионе).

3.       статистические уравнения зависимости;

4.       статистические индексы и др.                                                                           

Статистические индексы могут быть использованы в качестве меры изменения количества независимо от изменения качественного признака (цены, себестоимости, производительности труда и т.п.), а также для характеристики качественного признака независимо от изменения количества (объема продукции в натуральном выражении, численности работников и т.п.).

2. Классификация моделей и типы данных.

Модель – это приближенное описание реальных объектов, процессов, явлений в аспектах, интересующих исследователя.

классификация эконометрических моделей:

1) классификация эконометрических моделей по целевому назначению:

а) теоретико-аналитические модели, которые используются при исследовании общих свойств и закономерностей экономических процессов;

б) прикладные модели, которые используются при решении конкретных экономических задач (модели экономического анализа, прогнозирования, управления);

Также эконометрические модели могут быть использованы при исследовании различных сторон народного хозяйства и его отдельных частей.

2) классификация эконометрических моделей по исследуемым экономическим процессам и содержательной проблематике. При этом выделяются:

а) модели народного хозяйства в целом и его отдельных подсистем-отраслей, регионов и т. д.;

б) комплексы моделей производства и потребления;

в) комплексы моделей формирования и распределения доходов;

г) комплексы моделей трудовых ресурсов;

д) комплексы моделей ценообразования;

е) комплексы моделей финансовых связей и др.

3) классификация эконометрических моделей на дескриптивные и нормативные модели:

а) дескриптивные модели предназначены для объяснения наблюдаемых фактов или для построения вероятностного прогноза. В качестве примера дескриптивной модели можно привести производственные функции и функции покупательного спроса, построенные на основе обработки статистических данных;

ести модели оптимального планирования, характеризующие тем или иным образом цели экономического развития, возможности и средства их достижения;

4) классификация эконометрических моделей по характеру отражения причинно-следственных связей. При этом выделяют:

а) модели жестко детерминистские;

б) модели, в которых учитываются факторы случайности и неопределенности.

Вследствие перехода от жёстко детерминированных моделей к моделям второго типа, были разработаны реальные возможности успешного применения более совершенной методологии моделирования экономических процессов, учитывающих факторы случайности и неопределённости, а именно:

а) проведение многовариантных расчетов и модельных экспериментов с вариацией конструкции модели и ее исходных данных;

б) изучение устойчивости и надежности получаемых решений;

в) выделение зоны неопределенности;

г) включение в модель резервов;

д) применение приемов, повышающих приспособляемость (адаптивность) экономических решений к вероятным и непредвиденным ситуациям

В последнее время широко применяются эконометрические модели, непосредственно отражающие стохастичность и неопределенность экономических процессов. Данные модели используют соответствующий математический аппарат: теорию вероятностей и математическую статистику, теорию игр и статистических решений, теорию массового обслуживания, теорию случайных процессов.

5) Классификация эконометрических моделей по способам отражения фактора времени. При этом выделяют:

а) статические модели, характеризующие исследуемую зависимость между переменными на определённый момент времени;

б) динамические модели, характеризующие изменение экономических процессов во времени.

выделяются два типа выборочных данных:

·         Пространственная выборка (cross-sectional data) — набор экономических показателей, полученных в некоторый момент времени (иначе говоря, примерно в неизменных условиях), т.е. набор независимых выборочных данных из некоторой генеральной совокупности (так как практически независимость случайных величин проверить трудно, то обычно за независимые принимаются величины, не связанные причинно);

·         Временной (динамический) ряд (time-series data) — выборка, в которой важны не только сами наблюдаемые значения, но и порядок их следования друг за другом. Чаще всего данные представляют собой последовательные наблюдения одной и той же величины в последовательные моменты времени.

3. Этапы построения эконометрической модели.

Весь процесс эконометрического моделирования можно разбить на шесть основных этапов.

1-й этап (постановочный) - определение конечных целей моделирова­ния, набора участвующих в модели факторов и показателей, их роли;

2-й этап (априорный) - предмодельный анализ экономической сущности изучаемого явления, формирование и формализация априорной информации и исходных допущений, в частности относящейся к природе и генезису исходных статистических данных и случайных остаточных составляющих в виде ряда ги­потез;

3-й этап (параметризация) - собственно моделирование, т.е. выбор общего вида модели, в том числе состава и формы входящих в неё связей между переменными;

4-й этап (информационный) - сбор необходимой статистической информации, т.е. регистрация значений участвующих в модели факторов и показате­лей;

5-й этап (идентификация модели) - статистический анализ модели и в первую очередь статистическое оценивание неизвестных параметров модели Непосредственно связан с проблемой идентифицируемости модели, то есть ответа на вопрос «Возможно ли в принципе однозначно восстановить значения неизвестных параметров модели по имеющимся исходным данным в соответст-вии с решением, принятым на этапе параметризации?». После положительного ответа на этот вопрос необходимо решить проблему идентификации модели то есть предложить и реализовать математически корректную процедуру оценива­ния неизвестных параметров модели по имеющимся исходным данным;

6-й этап (верификация модели) — сопоставление реальных и модельных данных, проверка адекватности модели, оценка точности модельных данных.

Эконометрическое исследование включает решение следующих проблем

качественного анализа связей экономических переменных — выделения зависимых (yj) и независимых переменных (хi),

изучения соответствующего раздела экономической теории;

подбора данных;

спецификации формы связи между у и хi;

оценки параметров модели;

и т.д

4.Модель парной регрессии

Парная регрессия

Построение модели парной регрессия (или однофакторная модель) заключается в нахождении уравнения связи двух показателей у и х, т.е. определяется как повиляет изменение одного показателя на другой.

В задачах по эконометрике основным этапом является нахождение параметров модели и оценке их качества. Уравнение модели парной регрессииможно записать в общем виде:

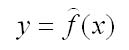
где у - зависимый показатель (результативный признак);

х - независимый, объясняющий фактор.

Линейные и нелинейные модели регрессии

Уравнение линейной регрессии: у = а + bx

Уравнения нелинейной регрессии

полиномиальная функция 

гиперболическая функция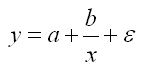 

степенная модель 

показательная модель 

экспоненциальная модель 

Определение параметров в моделях парной регрессии

Нахождение модели парной регрессии в эконометрике сводится к оценке уравнения в целом и по параметрам (a, b). Для оценки параметров однофакторной линейной модели используют метод наименьших квадратов (МНК). В МНК получается, что сумма квадратов отклонений фактических значений показателя у от теоретических ух минимальна

Сущность нелинейных уравнений, которые находятся в том случае, если нет линейных моделей, заключается в приведении их к линейному виду и как при линейных уравнениях решается система относительно коэффициентов a и b.

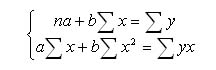
Для нахождения коэффициентов a и b в уравнении модели парной регрессии можно использовать формулы.

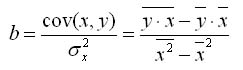
1. 5. Случайный член, причины его существования.

Рассмотрим простейшую линейную модель парной регрессии: y = a+bx+ε                

Величина y, рассматриваемая  как зависимая переменная, состоит из двух составляющих: неслучайной составляющей, а+bх и случайного члена ε.

Случайная величина ε называется также возмущением. Она включает влияние не учтенных в модели факторов, случайных ошибок и особенностей измерения.

Причин существования  случайной составляющей несколько.

1. Не включение объясняющих переменных. Соотношение между y и x является упрощением. В действительности существуют и другие факторы, влияющие на y, которые не учтены в форсуле. Влияние этих факторов приводит к тому, что наблюдаемые точки лежат вне прямой у = а+bх.

Часто встречаются факторы, которых следовало бы включить в регрессионное уравнение, но невозможно этого сделать в силу их количественной неизмеримости. Возможно, что существуют также и другие факторы, которые оказывают такое слабое влияние, что их в отдельности не целесообразно учитывать, а совокупное их влияние может быть уже существенным. Совокупность всех этих составляющих и обозначено в (2.1) через ε.

2. Агрегирование переменных. Рассматриваемая зависимость (2.1) – это попытка объединить вместе некоторое число микроэкономических соотношений. Так как отдельные соотношения,  имеют разные параметры, попытка объединить их является аппроксимацией. Аппроксима́ция, или приближе́ние — научный метод, состоящий в замене одних объектов другими, в том или ином смысле близкими к исходным, но более простыми. Наблюдаемое расхождение приписывается наличию случайного члена ε.

3. Выборочный характер исходных данных.  Поскольку исследователи чаще всего имеет дело с выборочными данными при установлении связи между у и х, то возможны ошибки и в силу неоднородности данных в исходной статистической совокупности. Для получения хорошего результата обычно исключают из совокупности наблюдения с аномальными значениями исследуемых признаков.

4. Неправильная функциональная спецификация. Функциональное соотношение между у и х математически может быть определено неправильно. Например, истинная зависимость может не являться линейной, а быть более сложной. Следует стремиться избегать возникновения этой проблемы, используя подходящую математическую формулу, но любая формула является лишь приближением истинной связи у и  х  и существующее расхождение вносит вклад в остаточный член.

5. Возможные ошибки  измерения.

1. 6. Условия нормальной линейной регрессии (Гаусса-Маркова)

Доказано, что для получения по МНК наилучших результатов (при этом оценки bi обладают свойствами состоятельности, несмещенности и эффективности) необходимо выполнение ряда предпосылок относительно случайного отклонения

Предпосылки использования метода наименьших квадратов (условия Гаусса – Маркова)

1. Случайное отклонение имеет нулевое математическое ожидание.

Данное условие означает, что случайное отклонение в среднем не оказывает влияния на зависимую переменную.

2. Дисперсия случайного отклонения постоянна.

Из данного условия следует, что несмотря на то, что при каждом конкретном наблюдении случайное отклонение ei может быть различным, но не должно быть причин, вызывающих большую ошибку.

3. Наблюдаемые значения случайных отклонений независимы друг от друга.

Если данное условие выполняется, то говорят об отсутствии автокорреляции.

4. Случайное отклонение д.б. независимо от объясняющей переменной.

Это условие выполняется, если объясняющая переменная не является случайной в данной модели.

5. Регрессионная модель является линейной относительно параметров, корректно специфицирована и содержит аддитивный случайный член.

6. Наряду с выполнимостью указанных предпосылок при построении линейных регрессионных моделей обычно делаются еще некоторые предположения, а именно:

- случайное отклонение имеет нормальный закон распределения;

-          число наблюдений существенно больше числа объясняющих переменных;

-          отсутствуют ошибки спецификации;

-          отсутствует линейная взаимосвязь между двумя или несколькими объясняющими переменными.

По лекции

1. В уравнении линейной модели y=a+bx+E

E-случайная величина, которая выражает характер, результирующий переменную y.

2. Математическое ожидание случайного члена в любом наблюдении равно 0, а дисперсия-постоянна.

3. Случайные члены для любых 2-х разных наблюдений- независимы ( некоррелированны)

4. Распределение случайного члена является нормальным.