Пусть заданы векторы в прямоугольной системе координат

тогда

Скалярное произведение векторов.

Определение. Скалярным произведением векторов и называется число, равное произведению длин этих сторон на косинус угла между ними.

 =   cos

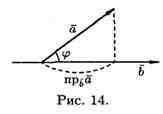
Свойства скалярного произведения

    1. Скалярное произведение обладает переместительным свойством: ab=ba

  

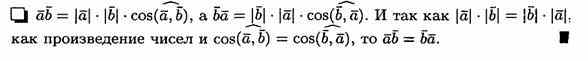
 Решение:                                                              

5. Если векторы а и b (ненулевые) взаимно перпендикулярны, то их скалярное произведение равно нулю, т. е. если a b, то ab=0. Справедливо и обратное утверждение: если ab=0 и а 0 b, то а  b

.

Выражение скалярного произведения через координаты

Пусть заданы два вектора

Найдем скалярное произведение векторов, перемножая их как многочлены (что законно в силу свойств линейности скалярного произведения) и пользуясь таблицей скалярного произведения векторов i, j, k:

   

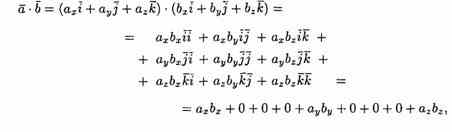
    т.е

Итак, скалярное произведение векторов равно сумме произведений их одноименных координат.

10. Векторное произведение. Свойства

Три некомпланарных вектора a, b и с, взятые в указанном порядке, образуют правую тройку, если с конца третьего вектора с кратчайший поворот от первого вектора а ко второму вектору b виден совершающимся против часовой стрелки, и левую, если по часовой (см. рис. 16).

      

 Векторным произведением вектора а на вектор b называется вектор с, который:

1. Перпендикулярен векторам a и b, т. е. са и сb;

2. Имеет длину, численно равную площади параллелограмма, построенного на векторах а и b как на сторонах (см. рис. 17), т. е. 

3.Векторы a, b и с образуют правую тройку.

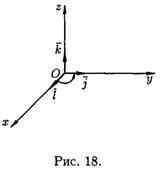
Векторное произведение обозначается а х b или [а,b]. Из определения векторного произведения непосредственно вытекают следующие соотношения между ортами i , j и k (см. рис. 18):

i х j = k,    j х k = i,    k х i = j.  Докажем, например, что iхj=k.

1) ki, kj;

2) |k|=1, но | i x j| = |i| • |J| • sin(90°)=1;

3) векторы i , j и k образуют правую тройку (см. рис. 16).

Свойства векторного произведения

1. При перестановке сомножителей векторное произведение меняет знак, т.е. а хb =(b хa ) (см. рис. 19).

 Векторы ахb и b ха коллинеарны, имеют одинаковые модули (площадь параллелограмма остается неизменной), но противоположно направлены (тройки а , b , а хb и a , b , bxa противоположной ориентации). Стало быть axb = -(bxa ).

2. Векторное произведение обладает сочетательным свойством относительно скалярного множителя, т. е. (а хb ) = (а ) х b = а х (b ).

Пусть >0. Вектор (ахb ) перпендикулярен векторам а и b . Вектор ( а)хb также перпендикулярен векторам а и b (векторы а, а лежат в одной плоскости). Значит, векторы (ахb ) и ( а)хb коллинеарны. Очевидно, что и направления их совпадают. Имеют одинаковую длину:

Поэтому (a хb )= ахb . Аналогично доказывается при <0.

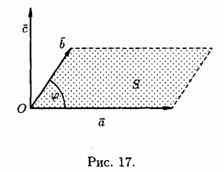
3. Два ненулевых вектора а и b коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору, т. е. а||b <=>ахb =0.

В частности, i *i =j *j =k *k =0.

4. Векторное произведение обладает распределительным свойством:

(a+b) хс= ахс+b хс.

Примем без доказательства.

Выражение векторного произведения через координаты

Мы будем использовать таблицу векторного произведения векторов i , j и k :

если направление кратчайшего пути от первого вектора к второму совпадает с направлением стрелки, то произведение равно третьему вектору, если не совпадает — третий вектор берется со знаком «минус».

Пусть заданы два вектора а=а_хi +a_yj +a_zk и b =b_xi +b_yj +b_zk . Найдем векторное произведение этих векторов, перемножая их как многочлены (согласно свойств векторного произведения):

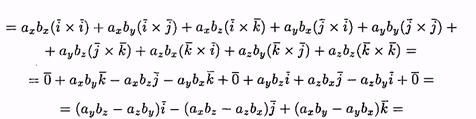
Полученную формулу можно записать еще короче:

Некоторые приложения векторного произведения

Установление коллинеарности векторов

Нахождение площади параллелограмма и треугольника

Согласно определению векторного произведения векторов а и b |а хb | = |а| * |b |sin , т. е. S _пар = |а х b |. И, значит, S =1/2|а х b |.