24. Приведение уравнения второго порядка к каноническому виду

25. Множества. Операции над множествами

Множество - это совокупность, набор элементов, объединенных общими свойствами.

Множества обозначаются заглавными латинскими буквами   , а элементы множества строчными латинскими буквами   .

Запись   означает, что есть множество   с элементами  , которые связаны между собой какой-то функцией   .

Замечание. Элементы в множество входят по одному разу, т.е. без повторений.

Основные операции:

1. Принадлежность элемента множеству:

где   -- элемент и   -- множество (элемент   принадлежит множеству   ).

2. Непринадлежность элемента множеству:

где   -- элемент и   -- множество (элемент   не принадлежит множеству   ).

3. Объединение множеств:   .

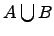Объединением двух множеств   и   называется множество   , которое состоит из элементов множеств   и   , т.е.

   или

4. Пересечение множеств:   .

Пересечением двух множеств   и   называется множество   , которое состоит из общих элементов множеств   и   , т.е.

   и

5. Разность множеств:   .

Разностью двух множеств   и   , например, множество   минус множество   , называется множество   , которое состоит из элементов множества   , которых нет в множестве   , т.е.

   и

6. Симметрическая разность множеств:   .

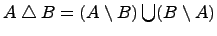Симметрической разностью двух множеств   и   называется множество   , которое состоит из не общих элементов множеств   и   , т.е.

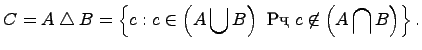
7. Дополнение множества:   .

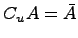Если предположим, что множество   является подмножеством некоторого универсального множества   , тогда определяется операция дополнения:

   и

8. Вхождение одного множества в другое множество:   .

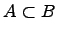Если любой элемент множества   является элементом множества   , то говорят, что множество   есть подмножество множества   (множество   входит в множество   ).

9. Не вхождение одного множества в другое множество:   .

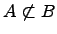Если существует элемент множества   , который не является элементом множества   , то говорят, что множество   не подмножество множества   (множество   не входит в множество   ).

26. Доказать: равномощность целых и рациональных чисел. Неравномощность действительных и натуральных чисел

1. Существующее правило: Множество натуральных чисел (N) равномощно множеству целых чисел (Z). Т.к. мы можем установить биекцию, т.е. занумеровать числа множества Z числами множества N так, что ни одно число не повторится и все окажутся пронумерованными. Делается это так: Целые числа: 0, 1, -1, 2, -2,…,+/-<><> Натуральные: 1, 2,  3, 4,  5,…,+<><> Видно что нечётные числа нумеруют ноль и отрицательные, а чётные – положительные. На этом основании делается вывод, что множества равны по мощности. 

Теорема: Множество R действительных чисел несчётно.

Доказательство:

(от противного)

Пусть множество действительных чисел счетно. Любое подмножество счетного множества тоже счетно. Возьмём на множестве действительных чисел интервал(0,1) и выкинем из этого отрезка числа, содержащие хотя бы в одном своём разряде нули или девятки.(Примеры таких чисел: 0.9, 0.0001 etc.) Множество A, составленное из оставшихся чисел является подмножеством множества R. Предположим, что множество A – счётно.

Тогда пронумеруем числа в разрядах:

0.a₁₁a₁₂a₁₃…

0.a₂₁a₂₂a₂₃…

……………

0.a_n1a_n2a_n3…

Теперь построим число b=0.b₁b₂…, причём b_i=a_ij+1(т. е. если a_ij=1, то b_i=2; а_ij=2 – то b_i=3). Таким образом построенное число b будет отличаться от каждого из чисел множества A хотя бы в одном разряде, и, следовательно не попадёт в составленный список. Тогда предположение неверно и множество A - несчётно.

Так как множество A является по условию подмножеством R, то и множество действительных чисел – несчётно. Теорема доказана.

Примечание: можно и не выбрасывать числа, содержащие 0 и 9. Т.о. в наш ряд некоторые числа войдут дважды. Это связано с тем, что конечные дроби могут быть превращены в бесконечные. Например:

½=0,5=0,5(0)=0,4(9)

0.01111…=1/2²+1/2³+1/2⁴…=lim = =1/2

В общем случае это могло стать причиной того, что не удалось сосчитать множество действительных чисел. Но множество чисел, представимых двояким образом (конечные дроби) – это подмножество рациональных чисел. Следовательно их счетное количество. Можно показать, что это множество эффективно перечислимо. Т.о. даже двойное представление множества таких чисел образует счетное мн-во, следовательно доказательство верно.

Определим рациональное число как q=n/m, где n и m – целые числа, причем m не равно 0.

Рассмотрим сначала положительные рациональные числа и запишем их в виде бесконечной матрицы, строки и столбцы которой пронумерованы натуральными числами начиная с 1. Элемент стоящий на пересечении i-ой строки и j-ого столбца получит наименование q_ij

1 2 3 4

1 q₁₁ q₁₂ q₁₃ q₁₄ …

2 q₂₁ q₂₂ q₂₃ q₂₄……

3 q₃₁ q₃₂ q₃₃ q₃₄……

4 q₄₁ q₄₂ q₄₃ q₄₄……

…………………………...

n q_n1 q_n2…………………

……………………………

Используя диагональный метод, перечислим их (пронумеруем натуральными числами):

q₁₁ q₂₁ q₁₂ q₁₃ q₂₂ q₃₁ q₄₁ q₃₂ q₂₃ q₁₄ q₁₅ q₂₄ q₃₃

1 2 3 4 5 6 7 8 9

Т.о. каждое рациональное число получит соответствующий номер, что означает счетность множества рациональных чисел.

Факт эффективной перечислимости множества Z напрямую следует из приведенного способа нумерации элементов натуральными числами.