
- •Методические указания к решению задачи №4.
- •Контрольная работа по предмету «Линейная алгебра» Вариант – 1
- •Контрольная работа по предмету «Линейная алгебра» Вариант – 2
- •Даны координаты векторов Найти:
- •Длину вектора ;
- •Контрольная работа по предмету «Линейная алгебра» Вариант - 3
- •Контрольная работа по предмету «Линейная алгебра» Вариант - 4
- •Контрольная работа по предмету «Линейная алгебра» Вариант - 5
- •Контрольная работа по предмету «Линейная алгебра» Вариант - 6
- •Контрольная работа по предмету «Линейная алгебра» Вариант - 7
- •Контрольная работа по предмету «Линейная алгебра» Вариант - 8
- •Контрольная работа по предмету «Линейная алгебра» Вариант - 9
- •Контрольная работа по предмету «Линейная алгебра» Вариант - 10
Контрольная работа по предмету «Линейная алгебра» Вариант - 3
Дана система линейных уравнений. Требуется показать, что система совместна и найти ее решение тремя способами: а) по формулам Крамера, выполнить проверку решения; б) методом Гаусса; в) методом обратной матрицы.
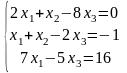
Решить матричные уравнения АХ = В и УА = В
 ;
;
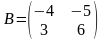
Даны координаты векторов Найти:
длину вектора ;
скалярное произведение векторов и ;
косинус угла между векторами и ;
векторное произведение векторов и ;
площадь параллелограмма и площадь треугольника , построенных на векторах и ;
смешанное произведение векторов , и ;
объем параллелепипеда и объем пирамиды , построенных на векторах , и .
-
(3; 1; –1), (–2; –1; 0), (5; 2; –1).
Выяснить, какие кривые определяются следующими уравнениями. Построить графики кривых.
а)
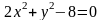 ; б)
; б)
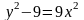 ; в)
; в)
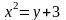 .
.Даны вершины треугольника
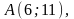
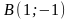 ,
,
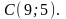 Найти:
Найти:
а) уравнения всех трех его сторон;
б) систему неравенств, определяющих множество точек, принадлежащих треугольнику, включая его стороны;
в) внутренний угол А;
г) длину высоты, проведенной из вершины ;
д) площадь треугольника.
Контрольная работа по предмету «Линейная алгебра» Вариант - 4
Дана система линейных уравнений. Требуется показать, что система совместна и найти ее решение тремя способами: а) по формулам Крамера, выполнить проверку решения; б) методом Гаусса; в) методом обратной матрицы.

Решить матричные уравнения АХ = В и УА = В
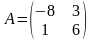 ;
;
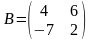
Даны координаты векторов Найти:
длину вектора ;
скалярное произведение векторов и ;
косинус угла между векторами и ;
векторное произведение векторов и ;
площадь параллелограмма и площадь треугольника , построенных на векторах и ;
смешанное произведение векторов , и ;
объем параллелепипеда и объем пирамиды , построенных на векторах , и .
-
(4; 3; 1), (6; 7; 4), (2; 0; –1).
Выяснить, какие кривые определяются следующими уравнениями. Построить графики кривых.
а)
 ; б)
; б)
 ; в)
; в)
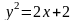
Даны вершины треугольника

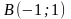 ,
,
 Найти:
Найти:
а) уравнения всех трех его сторон;
б) систему неравенств, определяющих множество точек, принадлежащих треугольнику, включая его стороны;
в) внутренний угол А;
г) длину высоты, проведенной из вершины ;
д) площадь треугольника.
Контрольная работа по предмету «Линейная алгебра» Вариант - 5
Дана система линейных уравнений. Требуется показать, что система совместна и найти ее решение тремя способами: а) по формулам Крамера, выполнить проверку решения; б) методом Гаусса; в) методом обратной матрицы.

Решить матричные уравнения АХ = В и УА = В
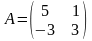 ;
;
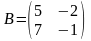
Даны координаты векторов Найти:
длину вектора ;
скалярное произведение векторов и ;
косинус угла между векторами и ;
векторное произведение векторов и ;
площадь параллелограмма и площадь треугольника , построенных на векторах и ;
смешанное произведение векторов , и ;
объем параллелепипеда и объем пирамиды , построенных на векторах , и .
-
(–3; 3; 1), (1; 0; –3), (2; 1; 6).
Выяснить, какие кривые определяются следующими уравнениями. Построить графики кривых.
а)
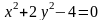 ; б)
; б)
 ; в)
; в)

Даны вершины треугольника
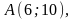
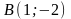 ,
,
 Найти:
Найти:
а) уравнения всех трех его сторон;
б) систему неравенств, определяющих множество точек, принадлежащих треугольнику, включая его стороны;
в) внутренний угол А;
г) длину высоты, проведенной из вершины ;
д) площадь треугольника.
