
- •Методические указания к решению задачи №4.
- •Контрольная работа по предмету «Линейная алгебра» Вариант – 1
- •Контрольная работа по предмету «Линейная алгебра» Вариант – 2
- •Даны координаты векторов Найти:
- •Длину вектора ;
- •Контрольная работа по предмету «Линейная алгебра» Вариант - 3
- •Контрольная работа по предмету «Линейная алгебра» Вариант - 4
- •Контрольная работа по предмету «Линейная алгебра» Вариант - 5
- •Контрольная работа по предмету «Линейная алгебра» Вариант - 6
- •Контрольная работа по предмету «Линейная алгебра» Вариант - 7
- •Контрольная работа по предмету «Линейная алгебра» Вариант - 8
- •Контрольная работа по предмету «Линейная алгебра» Вариант - 9
- •Контрольная работа по предмету «Линейная алгебра» Вариант - 10
Контрольные работы для студентов 1 курса направлений подготовки бакалавров 080100 - Экономика (профили: Экономика организации, Бухгалтерский учет и аудит) и 080200 Менеджмент
Индивидуальный номер варианта соответствует последней цифре номера зачетной книжки. Последняя цифра «0» соответствует десятому варианту.
Методические указания к решению задачи №4.
а)
Уравнение кривой получим, разделив обе части данного уравнения на 16:
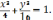
Получили
эллипс, полуоси которого  и
и  .
.
Построим эллипс (рис. 1).

б) 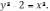
Уравнение кривой получим, разделив обе части данного уравнения на 2:

Получили
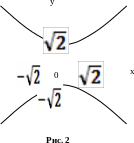
гиперболу с одинаковыми полуосями 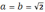 .
Фокусы гиперболы находятся на оси
.
Фокусы гиперболы находятся на оси  .
Уравнения асимптот
.
Уравнения асимптот 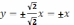 .
.
Строим гиперболу, причем сначала построим ее асимптоты (рис. 2).
в) 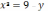 .
.
Уравнение кривой получим, преобразовав уравнение к виду
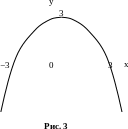
 Точка
Точка  – вершина параболы. Ветви параболы
направлены вниз. Парабола симметрична
относительно оси
.
– вершина параболы. Ветви параболы
направлены вниз. Парабола симметрична
относительно оси
.
Строим параболу (рис. 3).
Контрольная работа по предмету «Линейная алгебра» Вариант – 1
Дана система линейных уравнений. Требуется показать, что система совместна и найти ее решение тремя способами: а) по формулам Крамера, выполнить проверку решения; б) методом Гаусса; в) методом обратной матрицы.
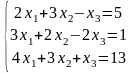
Решить матричные уравнения АХ = В и УА = В
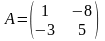 ;
;
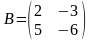
Даны координаты векторов
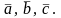 Найти:
Найти:
длину вектора
 ;
;скалярное произведение векторов
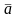 и
и
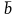 ;
;косинус угла между векторами и ;
векторное произведение векторов и ;
площадь параллелограмма
 и площадь треугольника
и площадь треугольника
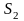 ,
построенных на векторах
и
;
,
построенных на векторах
и
;смешанное произведение векторов , и
 ;
;объем параллелепипеда
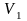 и объем пирамиды
и объем пирамиды
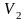 ,
построенных на векторах
,
и
.
,
построенных на векторах
,
и
.
-
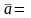 (2;
3; 1),
(2;
3; 1), 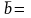 (2;
3; 4),
(2;
3; 4),  (3;
1; –1).
(3;
1; –1).
Выяснить, какие кривые определяются следующими уравнениями. Построить графики кривых.
-
а)
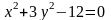 ; б)
; б)
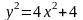 ; в)
; в)
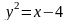
Даны вершины треугольника

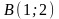 ,
,
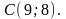 Найти:
Найти:
а) уравнения всех трех его сторон;
б) систему неравенств, определяющих множество точек, принадлежащих треугольнику, включая его стороны;
в) внутренний угол А;
г)
длину высоты, проведенной из вершины
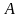 ;
;
д) площадь треугольника.
Контрольная работа по предмету «Линейная алгебра» Вариант – 2
Дана система линейных уравнений. Требуется показать, что система совместна и найти ее решение тремя способами: а) по формулам Крамера, выполнить проверку решения; б) методом Гаусса; в) методом обратной матрицы.
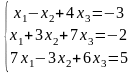
Решить матричные уравнения АХ = В и УА = В
 ;
;
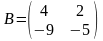
Даны координаты векторов Найти:
Длину вектора ;
скалярное произведение векторов и ;
косинус угла между векторами и ;
векторное произведение векторов и ;
площадь параллелограмма и площадь треугольника , построенных на векторах и ;
смешанное произведение векторов , и ;
объем параллелепипеда и объем пирамиды , построенных на векторах , и .
-
(1; –1; –3), (2; 3; 1), (2; 3; 4).
Выяснить, какие кривые определяются следующими уравнениями. Построить графики кривых.
а)
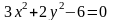 ; б)
; б)
 ; в)
; в)
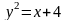
Даны вершины треугольника
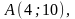
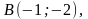
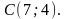 Найти:
Найти:
а) уравнения всех трех его сторон;
б) систему неравенств, определяющих множество точек, принадлежащих треугольнику, включая его стороны;
в) внутренний угол А;
г) длину высоты, проведенной из вершины ;
д) площадь треугольника.
