1.4.2. Прямокутна система

ДС на площині. Відмінність ДС на площині в прямокутній системі (від ДС в полярній системі), полягає в тому, що в них значення кута v відкладається вздовж осі ОХ, а функції f( v) або F(v) – вздовж осі ОY. Основними є наступні 8 варіантів представлення ДС на площині в прямокутній системі

Рис.1.27. Основні види ДС на площині в прямокутній системі

Розглянемо детальніше деякі з вказаних видів.

Нормовані ДС за напруженістю поля в прямокутній системі (на площині). Нижче приведені вказані ДС для деяких типів антен(рис.1.28)

ДС в прямокутній системі мають деякі переваги, причому основними є наступні:

• можна зменшити діапазон зміни кута v, збільшивши тим розрізнюючу здатність;

• можна представити ДС в логарифмічному масштабі, що корисно у випадку великого перепаду рівнів ГП та БП.

Рис. 1.28. ДС F(v) в прямокутній системі (СВ, ДГ, ЕГ)

ДС СВ отримані з використанням програми 1.5.

Програма 1.5.

figure ('Color','w');

Ln=0.625;

subplot(2,3,1);vr=[0:360]; v=vr./360*2*pi; b1=2*pi*Ln; b2=cos(b1);

b3=cos(b1.*cos(v))-b2;b4=(1-b2)*sin(v);f=abs(b3./b4);plot(vr,f);grid on;

axis([0 360 0 1.2]);xlabel('v');ylabel('|f(v)|');title('вісь CB,Ln=0.625');

а) б)

Рис. 1.29. ДС F(v) для СВ в прямокутній системі: лінійний масштаб (а); логарифмічний (б)

На рис.1.29 зменшено діапазон зміни кута v (порівняно з рис.1.26). що дозволило краще розрізнити ГП та БП.

На основі ДС в прямокутній системі також можна визначити ШГП(рис 1.30)

Рис. 1.30. ДС F(v) в прямокутній системі (СВ, ДГ, ЕГ) – визначення ШГП (2v_0.5)

Для визначення ШГП проведена допоміжна пряма на рівні F(v)=0.7. Її перетин з ДС вказує на ШГП, яка становить: для СВ при L_n=0.625 – 107^о-73^о =34^о; для ДГ– 136^о-44^о =92^о; для ЕГ – 67^о-(-67)=134^о;

ДС за кутовою густиною потужності в прямокутній системі (на площині). Нижче також приведені вказані ДС (рис. 1.31)

Рис. 1.31. ДС F²(v) в прямокутній системі (СВ, ДГ, ЕГ)

Порівнюючи ДС (рис1.26, рис.1.28) видно, що останні є більш вузькими. На основі даних ДС також можна визначити ШГП(рис 1.32)

Для визначення ШГП проведена допоміжна пряма на рівні F(v)=0.5. Її перетин з ДС вказує на ШГП, яка становить: для СВ при L_n=0.625 – 106^о-74^о =34^о; для ДГ– 135^о-45^о =90^о; для ЕГ – 65^о-(-65)=130^о. Отже, значення ШГП (2v_0.5), отримані згідно ДС (рис.1.30 та рис.1.30) повністю співпадають (з точністю до відліку результатів).

Рис. 1.32. ДС F²(v) в прямокутній системі (СВ, ДГ, ЕГ) – визначення ШГП (2v_0.5)

Нормовані ДС за напруженістю поля в прямокутній системі (просторові).

Нижче також приведені вказані ДС

Рис.1.33. ДС F(v) в прямокутній системі (СВ, ДГ, ЕГ), просторова та її проекції на площину (v, |F(v)|)

Фактично проекція просторової ДС F(v) в прямокутній системі на площину (|F(v)|, v) автоматично формує ДС на площині, яку немає необхідності будувати додатково.

Нормовані ДС за напруженістю поля в прямокутній системі (просторові) та визначення ШГП. Використовуючи просторові ДС в прямокутній системі можна просто визначити ШГП

а) б) в)

Рис.1.34. ДС СВ при L_n =0.5 (просторова, в прямокутній системі, з допоміжною площиною ) та її проекція на площину (v - |F(v)| ) при різних масштабах (б, в)

Якщо на нормованій просторовій ДС за напруженістю поля в прямокутній системі провести допоміжну площину на рівні F(v)=0.7, то можна отримати значення ШГП (2v_0.5). Для цього необхідно виконати проекцію просторової ДС на площину (v - F(v) ). Перевагою використання ДС в прямокутній системі для точнішого визначення ШГП є те, що по осі v можна змінювати масштаб (рис.1.34.б та рис.1.34,в) забезпечуючи необхідну розрізнючу здатність. Для аналогічних ДС в сферичній системі така зміна масштабу є неможливою.

Комбінована ДС в прямокутній системі. Як і для ДС в сферичній системі (рис.1.26) для ДС в прямокутній системі також можна сформувати комбіновані ДС(рис 1.35).

Але неоціненною перевагою комбінованих ДС в прямокутній системі є те, що на їх основі можна визначити динаміку зміни ШГП від L_n, тобто залежність 2v_0.5=f(L_n).

а) б) в)

Рис. 1.35. Комбінована ДС F(v) для СВ в прямокутній системі: її перерізи при L_n=const (a); проекція одного з перерізів на площину «v-|F(v)|» (б); просторова (в)

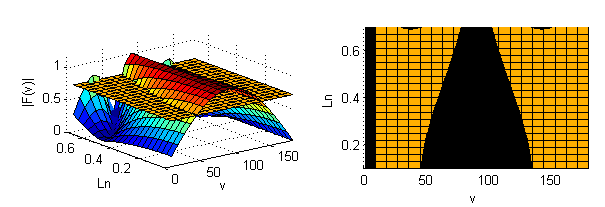
а) б)

Рис. 1.36. Комбінована ДС F(v) для СВ в прямокутній системі та її перетин площиною при F(v) =0.7 (a); проекція на площину «v –L_n |» (б)

Таким чином, комбінованою ДС є можливість отримання на її основі графічної залежності 2v_0.5=f(L_n), приведеної на рис. 1.36,б.