
- •1. Физические величины.
- •2. Система физических величин
- •4. Основные понятия кинематики.
- •5. Скорость материальной точки (мт).
- •6. Ускорение мт.
- •7. Понятие силы. Первый закон Ньютона.
- •8. Понятие массы тела. Второй закон Ньютона.
- •9. Третий закон Ньютона.
- •10. Скалярное и векторное произведения векторов.
- •11. Момент импульса и момент силы для материальной точки.
- •12. Уравнение движения для момента импульса.
- •13. Законы изменения и сохранения момента импульса.
- •14. Система материальных точек. Основные понятия.
- •15. Центр масс системы материальных точек.
- •16.Уравнение движения твердого тела.
- •17. Моменты инерции твердого тела относительно оси.
- •18. Момент инерции сплошного цилиндра.
- •19. Механические гармонические колебания – пружинный маятник.
- •20. Пружинный маятник с трением. Затухающие колебания.
- •21. Логарифмический декремент затухания и добротность.
- •22. Вынужденные колебания. Уравнение движения и его решение.
- •23. Вынужденные колебания. Резонанс.
- •24. Методы описания системы движущихся частиц.
- •25. Общее начало термодинамики.
- •26. Понятие температуры. Шкала температур.
- •27. Абсолютная термодинамическая шкала температур.
- •28. Внутренняя энергия системы.
- •29. Работа.
- •30. Теплота.
- •31. Первое начало термодинамики.
- •32. Калорическое и термическое уравнения состояния.
- •33. Теплоемкость.
- •34. Вывод соотношения для .
- •35. Вывод соотношения для в случае идеального газа.
- •36. Основные термодинамические процессы.
- •37. Основные термодинамические процессы для идеального газа.
- •43. Первое и второе начала термодинамики для элементарного процесса.
- •44. Термодинамический потенциал – внутренняя энергия u(s,V).
- •45. Термодинамический потенциал – свободная энергия u(s,V).
- •46. Термодинамический потенциал – потенциал Гиббса u(s,V).
- •47. Термодинамический потенциал – энтальпия u(s,V).
7. Понятие силы. Первый закон Ньютона.
Как показывает опыт, все материальные тела взаимодействуют друг с другом. В результате такого взаимодействия тела изменяют свою скорость, т.е. приобретают ускорение.
▼ Сила является векторной, количественной мерой взаимодействия между телами.

Все законы Ньютона являются обобщением большого числа опытных фактов.
▼ 1 закон Ньютона - существуют системы отсчёта, в которых свободные тела могут двигаться равномерно и прямолинейно или находиться в состоянии покоя.
▼ Свободными
называют тела, на которые не действуют
силы со стороны других тел, либо они
компенсируют друг друга для любого
момента времени (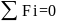 ).
).
▼ Система отсчета, о существовании которой утверждает 1 закон Ньютона, называется инерциальной системой отсчета (Пример - система Коперника).
▼ Система отсчета, которая движется с ускорением относительно инерциальной системой отсчета, называется неинерциальной системой отсчета (Пример - наша Земля).
8. Понятие массы тела. Второй закон Ньютона.
Из опыта следует, что если на разные тела подействовать одинаковой силой, то скорость их изменяется по-разному. Тела как бы по-разному сопротивляются, когда изменяют их скорость (Пример: теннисный шарик и гиря).
▼ Свойство тела оказывает сопротивление при изменении его скорости, называется инертностью тела.
▼ Масса теля является количественной, скалярной мерой инертности тела.
2 закон Ньютона.
▼ Импульсом
тела (или
кол-вом движения) называется векторная
величина импульса, равная произведению
массы тела на его скорость
 (1).
(1).
▼ 2
закон Ньютона для МТ
записывается в виде
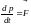 (2), где
(2), где
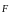 -
равнодействующая всех сил, действующих
на МТ.
-
равнодействующая всех сил, действующих
на МТ.
Закон в виде (2) справедлив также и для тел с переменной массой.
Рассмотрим случай, когда m = const (3).
Подставим
(1) в (2) и учтем (3) :
 ,
,
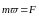 (4).
(4).
▼ 2 закон Ньютона имеет вид (4) для тел с постоянной массой. [F] = 1H = кг * м/cᶺ².
Left(4)
=
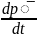 =
=
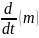 =
=
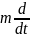 =
=
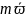
=
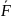 (5)
(5)
 - 2
закон Ньютона
- 2
закон Ньютона
9. Третий закон Ньютона.
Проиллюстрируем
вывод 3 закона Ньютона для системы двух
изолированных частиц.
 Две частицы взаимодействуют друг с
другом.
Две частицы взаимодействуют друг с
другом.
▼ Замкнутая система - система МТ-ек на которую не действуют внешние силы.
Опыт
показывает, что для такой системы
справедлив закон сохранения импульса
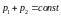 (1), где
(1), где
 и
и
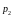 импульсы тел зависящих от времени (
импульсы тел зависящих от времени ( ).
).
Продифференцируем
неравенство (1)
:
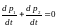 (2), к формуле
(2)
применим 2 закон Ньютона.
(2), к формуле
(2)
применим 2 закон Ньютона.
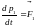 и
и
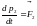 (3)
(3)
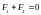 ,
,
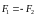 (4)
(4)
▼ Силы двух взаимодействующих МТ равны по величине, противоположны по направлению и действуют вдоль прямой соединяющей эти точки.
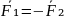 (5) –
3 закон Ньютона
(5) –
3 закон Ньютона
▼ Ньютон назвал F1 действием, а другую силу F2 противодействием.
▼ Поэтому иногда 3 закон Ньютона формулируется в следующем виде : сила действия равна и противоположна по направлению силе противодействия.
Обратим внимание, что эти силы приложены к разным телам, значит, о равновесии не может быть и речи.
Равновесие МТ тогда, когда сумма всех сил, действующих на МТ, равна нулю.
