9.Получение случайных чисел с произвольным законом распределения методом обратных функций.
М-д
обр ф-ий наиболее общий и универсальный
способ получения чисел, подчиненных
заданному закону. Стандартный
метод моделирования основан на том, что
интегральная функция распределения
любой
непрерывной случайной величины равномерно
распределена в интервале (0;1), т.е. для
любой случайной величины X
с
плотностью распределения f(x)
случайная
величина равномерно распределена на
интервале (0;1).
Тогда
случайную величину X
с произвольной плотностью распределения
f(x)
можно
рассчитать по следующему алгоритму:1.
Необходимо сгенерировать случайную
величину r
(значение случайной величины R),
равномерно распределенную в интервале
(0;1). 2. Приравнять
сгенерированное случайное число
известной функции распределения F(X)
и получить уравнение
.
3. Решая уравнение X=F-1(r),
находим искомое значение X
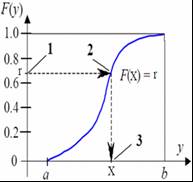
Графическое решение
.
10.Получение случайных чисел, подчиняющихся экспоненциальному закону
Экспоненциальное распределение. Непрерывная случайная функция, распределенная по экспоненциальному закону, имеет функцию распределения F(x) и плотность распределения f(x) вида:
(2.3)
(2.4)
Значения математического ожидания и дисперсии для экспоненциального закона распределения равны соответственно 1/λ и 1/λ^2.
Для
моделирования случайных величин xi
,имеющих экспоненциальное распределение,
можно воспользоваться непосредственным
решением уравнения
.
Действительно, с учетом (2.4) получаем:
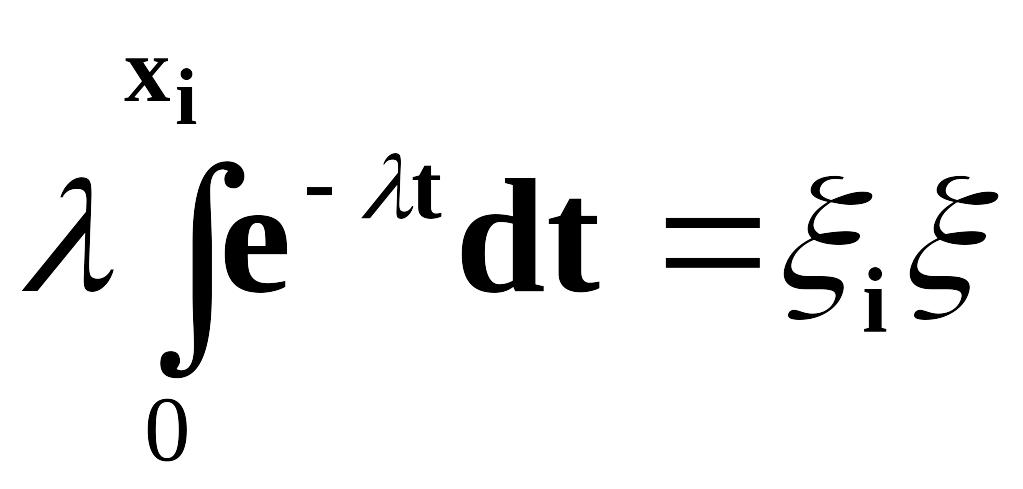(2.5)
После интегрирования имеем:
(2.6)
Поскольку случайная величина (1-i) имеет также равномерное распределение в интервале (0,1) окончательно получаем:
xi = -(1 / ) ln i = - ln i (2.7)
где альтернативной параметризацией является параметр масштаба θ=1/λ).
Алгоритм формирования значений случайной величины, распределенной по экспоненциальному закону:
1.Вводятся исходные значения: количество генерируемых величин N (не менее 100) и математическое ожидание экспоненциального закона распределения (THETA);
2.Обнуляется переменная К для подсчета количества генерируемых случайных величин;
3.Генератор псевдослучайных чисел формирует число;
4.Вычисляется случайная величина по формуле 2.7;
5.Значение величины выводится на печать;
6.Значение счётчика случайных величин увеличивается на единицу;
7.Процедура формирования случайных величин повторяется до тех пор, пока не будет получено заданное количество.