5.Черный ящик. Основная проблема моделирования

«Черным ящиком» называют систему внутренне содержание которого наблюдателю неизвестна, а доступны только вход и выход. Выбор этих входов и выходов и есть утверждающая часть модели, которая и будет определять организационную модель. Конечная цель – построение матем модели объекта, т.е. матем оператора А, связывающего выход с входом Компоненты называют факторами ли предикторами, а - откликом. Структуру оператора А мы не знаем. * - Внутренне содержимое скрыто от наблюдателя

Решением задачи «черным ящиком» называют идентификации системы в широком смысле. Основная задача – определение структуры системы, т.е. определение общего вида матем оператора, связ вход с выходом. 2-я задача – определение синтезов параметров. Это задача определения конкретных решений параметров, связывающий вход с выходом.

Идентификацию в узком смысле называют «серым ящиком». Предполагается точно известная структура системы и необходимо определить лишь ее неизвестный параментр по результатам эксперимента. (МНК предназначен для серого ящика, т.к. мы должны точно знать функцию). Многие прикладные задачи можно свести к задаче «серого ящика», использую матем системы.

Понимание эксперимента зависит от того, какая информация может быть получена из эксперимента системы.

Надо построить математическую модель, которая отражала бы зависимость , набор и выход . Векторный выход называется откликом, а функция - функция отклика.

Описание функционирования черного ящика сводится к соотношению между и – между откликами.

Пример:

М етод наименьших квадратов; степенной полином

1,2,3,4,5,6 2,4,6,8,10,12

7->7

2n+(n-1)(n-2)(n-3)(n-4)(n-5)(n-6)

78->734

Осн. проблема - Это выбор структуры, модели, описывающий черный ящик.

Трудность выбора математического выражения, определяющего структуру системы существенно зависит от априорного знания системы.

6.Общая схема моделирования

Моделированием наз-ся замещение одного объекта, назыв-го системой, др-м объектом, назыв-м моделью, и проведение экспериментов с моделью (или на модели), иссл-ие св-в модели, опираясь на рез-ты экспериментов с целью получения инф-ции о системе.

При модел-ии необх-мо обеспечить макс-ую эффек-ть модели системы. Эффек-ть обычно опр-ся как нек-ая разность м/ду какими-то показ-ми ценности рез-тов, получе-х в итоге эксплуатации модели, и теми затратами, кот-ые были вложены в ее разраб-ку и создание.

На базе системного подхода м. б. предложена и нек-рая послед-сть разработки моделей, когда выделяют две основные стадии проектир-ия: макропроект-ие и микропроект-ие.

На стадии макропроек-ия на основе данных о реальной системе S и внеш. среде Е строится модель внеш. среды, выявл-ся ресурсы и ограничения для построения модели системы, выбирается модель системы и критерии, позволяющие оценить адекватность модели М реальной системы S.

Стадия микропроек-ия в значит. степени зависит от конкр-го типа выбранной модели. В случ. имитационной модели необх-мо обеспечить созд-ие инф-ого, матем-го, технич-го и прогр-го обеспеч-ий систем модел-ия. На этой стадии м-но установить осн-ые хар-ки созданной модели, оценить время работы с ней : затраты ресурсов для получения заданного кач-ва соотв-ия модели пр-су функц-ия системы S.

Независимо от типа исп-мой модели М при ее построении необх-мо руководст-ся рядом принципов сист-го подхода: 1) пропорц-но-последов-ое продвиж-ие по этапам и направл-ям создания модели; 2) соглас-ие инф-ых, рес-сных, надежностных и др. хар-тик; 3) правильное соотн-ние отд-х ур-ней иерархии в системе модел-ния; 4) целостность отд-ых обособленных стадий постр-ия модели.

Модель М должна отвечать заданной цели ее создания, поэтому отд-ые части д-ны компоноваться взаимно, исходя из единой системной задачи. Цель м. б. сформулирована качественно, тогда она будет обладать большей содержательностью и длительное время м-т отображать объективные возм-сти данной системы моделирования.

При колич-ой формулировке цели возникает целевая функция, которая точно отображает наиб. существенные ф-ры, влияющие на достижение цели. Целевую ф-ию можно представить в виде U₁=F(X, Y, U₂….U_n) , где Х-входы, У-выходы, U₁, U₂…U_n – ограничения цели; при чем задача стоит в оптимизации U₁. Оптимиз-ся может более одного критерия. Для упрощения модели М цели делят на подцели и создают более эфф-ные виды моделей в завис-ти от полученных подцелей модел-ия.

Для правильно построенной модели М характерным явл-ся то, что она выявляет лишь те закономерности, которые нужны исследователю, и не рассматривает свойства системы S, не существенные для данного иссл-ия. Модель выступает как нек-ый «заместитель» оригинала, обеспечивающий фиксацию и изучение лишь нек-ых св-в реального объекта. Искусство моделирования – выделение существенного из множества несущественного.

Заключит-ный этап моделирования — анализ модели. По полученным расчетным данным проверяется, наск-ко расчеты отвечают нашему представлению и целям моделирования. На этом этапе определяются рекомендации по совершенствованию принятой модели и, если возможно, объекта или процесса.

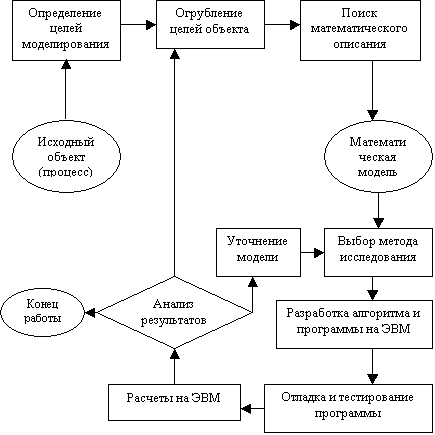
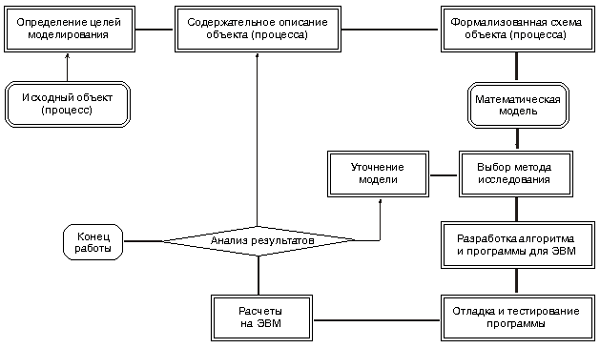
1. Определение целей моделирования. Основные из них, как предлагает А.Б. Горстко [3], таковы:

1) модель нужна для того, чтобы понять, как устроен конкретный объект, какова его структура, основные свойства, законы развития и взаимодействия с окружающим миром;

2) модель нужна для того, чтобы научиться управлять объектом (или процессом) и определить наилучшие способы управления при заданных целях и критериях;

3) модель нужна для того, чтобы прогнозировать прямые и косвенные последствия реализации заданных способов и форм воздействия на объект.

Естественно, прежде чем формулировать цель исследования, необходимо всесторонне изучить структуру моделируемого объекта (процесса).

2.Содержательное описание (огрублении целей объекта) в словесной форме согласно Н.П. Бусленко содержит [16]:

сведения о физической природе исследуемого процесса;

сведения о количественных характеристиках элементарных явлений исследуемого процесса;

сведения о месте и значении каждого элементарного явления в общем процессе функционирования рассматриваемой системы;

постановку прикладной задачи, определяющую цели моделирования исследуемого процесса.

Содержательное описание процесса обычно самостоятельного значения не имеет, а служит лишь основой для дальнейшей формализации этого процесса — построения формализованной схемы и математической модели процесса.

3.Формализованная схема является промежуточным звеном между содержательным описанием и математической моделью и разрабатывается в тех случаях, когда из-за сложности исследуемого процесса переход от содержательного описания к математической модели оказывается невозможным. На этапе построения формализованной схемы должна быть дана точная математическая задачи исследования с указанием окончательного перечня искомых величин и оцениваемых зависимостей. Прежде всего составляется список величин, от которых зависит поведение объекта или ход процесса, а также тех величин, которые желательно получить в результате моделирования. Обозначив первые (входные) величины через x1, x2, …, xn; вторые (выходные) через y1, y2, …, yk, можно поведение объекта или процесса символически представить в виде yj = Fj(x1, x2, …, xn) (j = 1, 2, …, k), где Fj символически обозначает некоторые математические операции над входными величинами.

Важнейшим этапом моделирования является разделение входных параметров по степени важности влияния их изменений на выходные. Такой процесс называется ранжированием. Чаще всего невозможно, да и не нужно, учитывать все факторы, которые могут повлиять на значения интересующих нас величин yj. От того, насколько умело выделены важнейшие факторы, зависит успех моделирования, быстрота и эффективность достижения цели. Отбрасывание (по крайней мере, при первом подходе) менее значимых факторов огрубляет объект моделирования и способствует пониманию его главных свойств и закономерностей.

4.На этапе перехода от формализованной схемы к математической модели необходимо перейти от абстрактной формулировки модели к формулировке, имеющей конкретное математическое наполнение. В этот момент модель предстает перед нами в виде уравнения, системы уравнений, системы неравенств, дифференциального уравнения или системы таких уравнений и т.д. Утверждается, что "для преобразования формализованной схемы в модель необходимо прежде всего, воспользовавшись соответствующими схемами, записать в аналитической форме все соотношения, выразить все логические условия. Последним этапом формализации является идентификация модели — определение параметров и структуры модели, обеспечивающей наилучшее совпадение исходных данных объекта и данных, полученных на модели объекта".

5.Когда математическая модель сформулирована, и выполнена ее идентификация, выбирается метод исследования модели.

6.Разработка алгоритма и составление программы для ЭВМ — творческий и трудно формализуемый процесс. В настоящее время достаточно распространенным подходом к программированию остается структурный подход, основными приемами которого являются модульность, использование лишь базовых алгоритмических структур, разработка алгоритма "сверху вниз" с дальнейшей пошаговой детализацией. Другим, не менее (а может быть, более) популярным подходом является объектно-ориентированное программирование. Графический пользовательский интерфейс целесообразно реализовывать, используя визуальные возможности программирования. В последнее время такой подход нашел широкое распространение в связи с увеличением быстродействия ЭВМ, многие из которых работают под управлением графических операционных систем. Относительная простота изучения и "кнопочная" технология, когда создание интерфейса программы значительно ускоряется, делают эти средства привлекательными для создания демонстрационных программ. Для постановки научных численных экспериментов по-прежнему целесообразнее использовать более традиционные средства, т.к. здесь наиболее важной является скорость вычислений, а не оформление программы. В некоторых случаях расчеты удобно провести, используя готовые программные продукты, например, электронные таблицы или специальные математические пакеты.

7.После составления программы с ее помощью решается простейшая тестовая задача (желательно, с заранее известным ответом) с целью отладки и тестирования программы, устранения грубых ошибок [2]. Затем следует собственно численный эксперимент.

8.В случае несоответствия модели реальному процессу происходит возврат к одному из предыдущих этапов. Возможные точки возврата указаны на схеме: либо в процессе огрубления были отброшены какие-то важные факторы или же было взято слишком много незначительных факторов и требуется уточнить математическую модель; либо выбор метода исследования оказался не слишком удачным и нужно использовать более сложный и точный. После внесения тех или иных изменений вновь проходим по части технологической цепочки и делаем это до тех пор, пока не будут получены приемлемые результаты.

9.По окончанию компьютерного эксперимента с математической моделью накопленные результаты (чаще всего численные) обрабатываются тем или иным способом (опять же с помощью компьютера) и интерпретируются. Чаще удобной для восприятия формой представления результатов являются не таблицы значений, а графики, диаграммы. Иногда численные значения пытаются заменить аналитически заданной функцией, вид которой определяет экспериментатор. Обработанные данные в конечном итоге попадают в отчет (или научную статью) о проделанном эксперименте.