
- •8. Математические модели приводов (сервоприводов) исполнительных механизмов.
- •Математические модели датчиков координат и информационных преобразователей.
- •10. Математические модели типовых регуляторов суим.
- •1. Пропорциональный регулятор (п-регулятор).
- •2. Интегральный регулятор (и-регулятор).
- •3. Дифференциальный регулятор (д-регулятор).
- •4. Пропорционально-интегральный регулятор (пи-регулятор).
- •6. Пропорционально-интегрально-дифференциальный регулятор (пид-регулятор).
4. Пропорционально-интегральный регулятор (пи-регулятор).
 Принципиальная
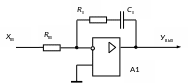
схема регулятора приведена на рис. 4.32.
Принципиальная
схема регулятора приведена на рис. 4.32.
Рис. 4.32. Принципиальная электрическая схема ПИ-регулятора
Передаточная функция регулятора
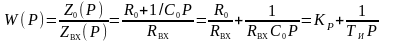 , (4.41)
, (4.41)
где KР – коэффициент передачи регулятора, KР = R0/Rвх;
Tи – постоянная времени интегратора, Tи = RвхС0 .
Переходная характеристика регулятора:
Увых(t) = Увых(0) + [KР + t/(RВХС0)]˖1(t), Увых(0) = 0.
Переходный процесс в регуляторе будет иметь вид, изображенный на рис. 4.33.

Рис. 4.33. Переходный процесс в ПИ-регуляторе
Функциональная схема пропорционально-интегрального регулятора приведена на рис. 4.34.
Передаточную функцию ПИ-регулятора часто представляют не в виде суммы двух слагаемых, а в виде так называемого изодромного звена
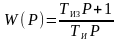 , (4.42)
, (4.42)
где TИЗ – постоянная времени изодромного звена, TИЗ = R0C0 ,
TИ – постоянная времени интегрирования регулятора, TИ = RВХC0 .
ПИ-регулятор, включенный в структуру САУ, обеспечивает компенсацию одной большой постоянной времени объекта управления.

Рис. 4.34. Функциональная схема
ПИ-регулятора
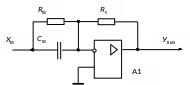
5. Пропорционально-дифференциальный регулятор (ПД-регулятор) Принципиальная схема регулятора приведена на рис. 4.35.
Рис. 4.35. Принципиальная электрическая схема ПД-регулятора
Передаточная функция регулятора
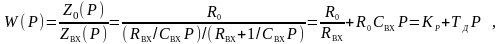 (4.43)
(4.43)
где KР – коэффициент передачи регулятора, KР = R0/RВХ;
TД – постоянная времени интегратора, TД = R0СВХ.
Переходная характеристика регулятора:
Увых(t) = KР˖1(t) + TД(t), где (t) – дельта-функция Дирака.
Переходный процесс в ПД-регуляторе будет иметь вид, изображенный на рис. 4.36, функциональная схема регулятора приведена на рис. 4.37.
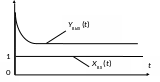 Рис.
4.36. Переходный процесс в ПД-регуляторе
Рис.
4.36. Переходный процесс в ПД-регуляторе

Рис. 4.37. Функциональная схема
ПД-регулятора
6. Пропорционально-интегрально-дифференциальный регулятор (пид-регулятор).
 Принципиальная
схема регулятора приведена на рис. 4.38.
Принципиальная
схема регулятора приведена на рис. 4.38.
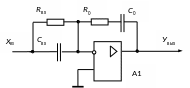
Рис. 4.38. Принципиальная электрическая схема ПИД-регулятора
Передаточная функция регулятора
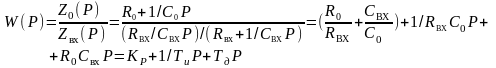 (4.44)
(4.44)
где KР – коэффициент передачи регулятора, Kр = R0/Rвх + CВХ/С0;
Tи – постоянная времени интегрирования, TИ = RВХС0;
Tд – постоянная времени дифференцирования, TД = R0СВХ.
Временная характеристика регулятора:
Увых(t) = Увых(0) + KР · 1(t) + (1/TиP) · 1(t) · t + TД(t),
где (t) – дельта-функция Дирака, Увых(0) = 0.
Переходный процесс в регуляторе будет иметь вид, изображенный на рис. 4.39, функциональная схема приведена на рис. 4.40.
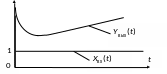
Рис. 4.39. Переходный процесс
в ПИД-регуляторе

Рис. 4.40. Функциональная схема
ПИД-регулятора
По аналогии с ПИ-регулятором ММ ПИД-регулятора часто представляют в виде изодромного звена второго порядка
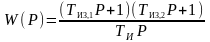 , (4.45)
, (4.45)
где ТИЗ,1, ТИЗ,2 – постоянные времени изодромного звена; Тиз,1 = R0С0 , ТИЗ,2 = RвхСвх.
На практике часто применяются иные схемы ПД- и ПИД-регуляторов, обеспечивающие реальное дифференцирование ошибки регулирования и, соответственно, более высокую помехозащищенность системы.
ПИ-регулятор в компенсационных системах управления обеспечивает компенсацию одной большой постоянной времени объекта управления, а ПИД-регулятор – двух больших постоянных времени, обеспечивая тем самым форсирование динамических процессов и улучшение динамики СУИМ. Регуляторы, содержащие более одного интегратора, призваны обеспечить астатизм СУИМ при аддитивных воздействиях не только в виде ступенчатой функции времени, но и в виде временной функции более сложного вида. ПДД регуляторы применяют в СУИМ интегрирующего типа.
Регуляторы включают, как правило, последовательно с объектом управления. Они призваны скорректировать динамику СУИМ с целью удовлетворения требованиям к ее статическим и динамическим показателям. При синтезе СУИМ вместо понятия «регулятор» часто применяют понятие «корректирующее устройство» («корректирующее звено»), включаемое последовательно с объектом управления или его частью, иногда – в обратной связи по регулируемой координате.
