Домашнє завдання

1. Виконати арифметичні операції додавання/віднімання у прямому, оберненому та додатковому модифікованих кодах:

А) Х+У

Б) Х-У

В) –Х+У

Г) –Х-У

Х=(@+12)₁₀

У= (@+25)₁₀

де @ - порядковий номер по журналу, або останні дві цифри студентського квитка.

Тема 1.2 Множення та ділення в еом

Лекція №3с. Прискорене множення

Прискорення операції множення дозволяє істотно підвищити продуктивність ЕОМ, оскільки приблизно 70% свого часу вони витрачають на виконання цієї операції. Можливі шляхи скорочення часу множення: зменшення часу додавання і зсуву кодів; зменшення кількості додавань і кількості зсувів кодів.

Оскільки прості методи множення передбачають виконання в кожному циклі зсув кодів тільки на один розряд, то зменшити час зсуву неможливо тому, що кола для зсуву реалізують, як правило, з найменшою затримкою сигналів.

Зменшення часу додавання двох кодів досягається за рахунок ускладнення кіл формування розрядних сум і перенесень у суматорі. Але це ні яким чином не впливає на організацію процесу множення. Тому основні підходи щодо прискорення операції множення базуються на зменшенні кількості додавань і кількості зсувів кодів. Відомі на цей час методи прискорення множення розподілені на дві великі групи: логічні й апаратні.

Логічними методами прискорення множення називають такі методи, реалізація яких не вимагає змін основної структури арифметичних кіл пристрою для множення, а прискорення досягається тільки за рахунок ускладнення схеми керування цим пристроєм. Стосовно пристроїв для множення паралельних кодів ознакою того, що ми маємо справу з логічним методом прискорення множення, є незалежність кількості додаткової апаратури (у порівнянні з вихідною схемою) від кількості розрядів співмножників.

Апаратні методи, прискорення множення вимагають для свого здійснення введення додаткової апаратури в основні арифметичні кола пристрою для множення.

Розрізняють апаратні методи першого порядку і другого порядку. Для апаратних методів першого порядку характерна лінійна залежність кількості додаткової апаратури від кількості розрядів у співмножниках п. Тоді як реалізація методів другого порядку вимагає введення додаткової апаратури, кількість якої пропорційна .

Логічні методи прискорення операції множення

До логічних методів прискорення операції множення належать: метод множення з пропусканням додавань у тих випадках, коли чергова цифра множнику є нуль; метод множення з перетворенням цифр множнику шляхом групування розрядів i метод множення з послідовним перетворенням цифр множника.

В основі двох останніх логічних методів лежить перехід до надлишкової двійкової системи числення з алфавітом {1, 0, }, який дозволяє зменшити кількість одиниць у коді множника, але при цьому в процесі множення будуть виконуватись операції додавання та віднімання.

Метод множення з пропусканням додавань є найпростішим з логічних методів прискорення множення. Схему керування взагалі простіше побудувати так, щоб за тактом зсуву щораз приділявся час на додавання, але додавання виконувалося б у залежності від цифри множника. Невелике ускладнення схеми керування, що дозволяє відводити час на додавання тільки тоді, коли воно дійсно необхідно, скорочує число тактів додавання в середньому вдвічі.

Цей метод прискорення рівною мірою підходить для тих випадків, коли множення починається зі старших розрядів множника, і для випадків, коли множення починається з молодших розрядів.

Приклад 1. Помножити числа А = - 0, 10100 і В = 0, 10011, використовуючи метод множення з пропусканням додавань.

Розв'язання. Для даних чисел маємо: =1; = 0, 10100; =0; = 0, 10011. Визначаємо знак добутку: =1 0=1.

Усі дії, що виконуються в кожному циклі множення, наведені табл. 1.

Відповідь: С= - 0, 0101111100.

Таблиця 1 - Приклад множення за прискореним методом

Розглянемо тепер метод множення з перетворенням цифр множнику шляхом групування розрядiв.

Кількість циклів, що необхідні для реалізації операції множення, можна скоротити, якщо в кожному циклі аналізувати не один, а два або більше розрядів множнику, виконуючи після аналізу додавання або віднімання та зсув множнику на відповідну кількість розрядів (два або більше). Для організації прискореного множення множник розбивають на групи з двох розрядів і перетворюють його таким чином, щоб кожна група містила не більш одної значущої одиниці (додатної або від'ємної).

Правила перетворення множника з молодших розрядів у разі групування по два розряди формулюються, враховуючи таке.

Комбінації 00, 01, 10 не перетворюються, а комбінація 11 замінюється комбінацією 1.0 , яка містить від'ємну одиницю в даній групі розрядів і додатну одиницю, що передається до наступної групи розрядів множника.

З урахуванням одиниці, що передається з попередньої групи розрядів, у даній групі розрядів після перетворення може зустрітися одна з таких комбінацій:

00 - якщо дана група розрядів містить цифри 00 і з попередньої групи одиниця не передається або якщо дана група розрядів містить цифри 11 і одиниця передається з попередньої групи розрядів;

01 - якщо дана група містить цифри 01 і з попередньої групи одиниця не передається, або якщо дана група розрядів містить 00 і передається одиниця з попередньої групи розрядів;

10 - якщо дана група містить 10 і нема одиниці з попередньої групи або якщо дана група містить 01 і є одиниця з попередньої групи розрядів;

0 - якщо дана група розрядів містить 11 і нема одиниці з попередньої групи або якщо дана група містить 10 і є одиниця з попередньої групи.

Із сказаного випливають правила перетворенням множнику, починаючи з молодших груп розрядів, що наведені в табл. 2. Тут - цифри даної групи розрядів; - цифра, що передається з попередньої групи; - перетворені цифри даної групи; - цифра, що передається в наступну групу.

Таблиця 2 - Правила перетворенням множнику, починаючи з молодших груп розрядів

0 0	0	0 0	0	0 0	1	0 1	0
0 1	0	0 1	0	0 1	1	1 0	0
1 0	0	1 0	0	1 0	1	0	1
1 1	0	0	1	1 1	1	0 0	1

Застосовуючи ці правила необхідно враховувати, що старша значуща цифра перетвореного множника може знаходитися в розряді цілих, де не перетворений множник містить завжди нуль.

Приклад 2. Використовуючи групування розрядів, виконати перетворення множнику 001011111001100111, починаючи з молодших розрядів.

Розв'язання. Діючи за правилами, що наведені в табл. 3.14, одержимо

0 0	1 0	1 1	1 1	1 0	0 1	1 0	0 1	1 1
+1	+1	+1	+0	+0	+0	+0	+1
0 1	0	0 0	0	1 0	0 1	1 0	1 0	0

Замість 11 одиниць у вихідному представленні множника одержуємо 8 додатних і від'ємних одиниць у перетвореному.

Відповідь: 010 000 100110100 .

Коли одразу аналізуються два розряди перетвореного множнику, то в процесі множення виконуються такі дії.

Якщо група містить комбінацію 00, то це означає, що протягом двох найближчих циклів множення не потрібно буде виконувати ні додавань, ні віднімань; при наявності комбінації 01 потрібно буде виконати одне додавання в першому з двох найближчих циклів множення, а у разі комбінації 10 - у другому. Коли група містить комбінацію 0 , то буде потрібно виконати одне віднімання в першому з двох найближчих циклів множення.

У разі одночасного аналізу двох розрядів, починаючи зі старших, у правилах перетворення груп розрядів (табл. 3.15) враховується значення сусіднього розряду, що розташований праворуч від групи, яка аналізується. При цьому аналіз розрядів множника завжди починається з пустої групи, що дописується ліворуч від найстаршого розряду.

Приклад 3. Використовуючи групування розрядів, виконати перетворення множнику 001011111001100111, починаючи зі старших розрядів.

Розв'язання. Діючи за правилами, що наведені в табл. 3., одержимо

Замість 11 одиниць у вихідному представленні множника одержуємо 7 додатних і від'ємних одиниць у перетвореному.

Відповідь: 010 0000 010 0100 .

Той чи інший метод перетворення тим ефективніше, чим менше в перетвореному множнику середня кількість додатних і від'ємних одиниць, тобто чим менше в середньому потрібно додавань і віднімань. Важлива також максимальна кількість додавань і віднімань, що можуть виконуватись під час множення.

Таблиця 3 - Правила перетворення множнику, починаючи зі старших груп розрядів

0 0	0	0 0	0 0	1	0 1
0 1	0	0 1	0 1	1	1 0
1 0	0	0	1 0	1	0
1 1	0	0	1 1	1	0 0

Для оцінки ефективності описаного вище методу групування розрядів відзначимо насамперед, що для будь-якої комбінації цифр протягом двох циклів множення може бути не більш одного додавання або віднімання. Таким чином, в гіршому випадку кількість додавань-віднімань дорівнює 0,5п.

Метод множення з послідовним перетворенням цифр множника передбачає послідовний аналіз цифр множника без розбиття на групи. При цьому використовується такі правила перетворення:

- якщо дана цифра неперетвореного множника не збігається із сусідньою праворуч цифрою, сусідня ліворуч цифра є 0 і попередня цифра перетвореного множника є 0, то даний розряд у перетвореному множнику є 1;

- якщо дана цифра неперетвореного множника не збігається із сусідньою праворуч цифрою, сусідня ліворуч цифра є 1 і попередня цифра перетвореного множника є 0, то даний розряд перетвореного множника повинний містити ;

- якщо дана цифра неперетвореного множника збігається із сусідньої праворуч цифрою або якщо попередня цифра перетвореного множника не є нулем, то даний розряд у перетвореному множнику є 0.

Застосовуючи ці правила необхідно враховувати, що старша значуща цифра перетвореного множника може знаходитися в розряді цілих; праворуч і ліворуч від значущих розрядів перетвореного множника завжди передбачаються нулі. Коли в приведеному правилі говориться про "попередні" цифри перетвореного множника, то стосовно до множення від молодших розрядів це відноситься до попередньої молодшої цифри перетвореного множника, а стосовно до множення від старших - до старшої попередньої цифри.

Описане послідовне перетворення розрядів множнику забезпечує під час множення в середньому 0,333п додавань-віднімань. Це найкращий результат, що може бути отриманий для логічних методів прискорення множення.

У здійсненні метод послідовних перетворень ненабагато складніше, ніж метод групування розрядів множника, ефективність же його вище.

При цьому виникають визначеної довжини послідовності чи нулів одиниць, що приводить до необхідності одночасного аналізу декількох розрядів множника і зрушенню на довільне число розрядів.

Апаратні методи прискорення операції множення

Спочатку розглянемо апаратні методі прискорення операції множення першого порядку.

1. Метод множення з перетворенням цифр множнику групування розрядiв і використанням кратних множеного.

Практично використовують розбиття на групи з чотирьох розрядів, що рівносильне переходу до шестнадцаткової системи числення. При цьому розглядається чергова цифра (тетрада) множника і його попередня цифра (тетрада). В залежності від значень цифри множнику в попередньому розряді виконуються різні дії (табл.4). Для реалізації такого множення потрібно попередньо сформувати кратні множеного: А, 2А, 3А і 6А.

Аналіз чотирьох двійкових розрядів одночасно дає можливість одразу здійснити зсув на чотири розряди.

Таблиця 4 - Дії, що виконуються в залежності від цифр множника

Тетрада, що аналізується	Значення попередньої цифри		Тетрада, що аналізується		Значення попередньої цифри
	8	<8			8	<8
0 0 0 0	+А	0		1 0 0 0		- (6А+А)	+(6А+2А)
0 0 0 1	+2А	+А		1 0 0 1		- 6А	- (6А+А)
0 0 1 0	+3А	+2А		1 0 1 0		- (3А+2А)	- 6А
0 0 1 1	+(2А+2А)	+3А		1 0 1 1		- (2А+2А)	- (3А+2А)
0 1 0 0	+(3А+2А)	+(2А+2А)		1 1 0 0		- 3А	- (2А+2А)
0 1 0 1	+6А	+(3А+2А)		1 1 0 1		- 2А	- 3А
0 1 1 0	+(6А+А)	+6А		1 1 1 0		- А	- 2А
0 1 1 1	+(6А+2А)	+(6А+А)		1 1 1 1		0	- А

2. Метод множення з аналізом довільної кількості розрядiв множнику. Ідея методу полягає у виявленні послідовностей нулів і одиниць з наступної груповою обробкою розрядів множнику. Якщо виявляється група вигляду , то виконується одразу зсув на k-1 розрядів і додавання множеного. Якщо аналізується група вигляду , то здійснюється зсув одразу на k-1 розрядів і віднімається множене. Коли аналізується група розрядів вигляду , то виконується її перетворення в нову групу вигляду . Код цієї групи показує, що спочатку виконується віднімання множеного, а потім зсув одразу на k-1 розрядів.

Такий метод прискорення операції множення вимагає створення пристрою для зсуву кодів на довільну кількість розрядів.

3. Метод множення з розбиттям множника на частини передбачає одночасне виконання множення числа А на окремі частини числа В з наступним додаванням отриманих результатів.

Множник В можна розбити на будь-яку кількість частин, але найефективнішим, з точки зору комплексної оцінки апаратних і часових витрат, є розбиття на дві частини. Для цього випадку обчислення описуються такою формулою:

.

Якщо множення на частини виконується за першим і другим методами, то час множення дорівнює:

.

4. Метод множення з використанням таблиць квадратів чисел базується на тотожності:

.

За значеннями суми і різниці співмножників з таблиці квадратів чисел зчитуються числа і , а потім остаточний добуток формується шляхом виконання операції віднімання .

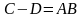Різновид цього методу множення описується тотожністю

.

Практично даний метод і його різновид дозволяють прискорити виконання операції множення чисел тільки невеликої розрядності (8 або 16 розрядів), тому що зі збільшенням розрядності чисел складність таблиці значно зростає.

4. Метод множення з запам’ятовуванням проміжних перенесень.

Час множення можна скоротити шляхом зменшення тривалості кожного додавання за рахунок виключення з нього часу, що витрачається на розповсюдження перенесень. Суть цього методу прискорення полягає в тому, що весь процес одержання добутку виконується додаванням без розповсюдження перенесень з одночасним їх запам'ятовуванням і однократним розповсюдженням перенесень на заключному етапі множення. При цьому в кожному циклі множення додаються порозрядно три числа: черговий частковий добуток, проміжна сума часткових добутків і проміжні перенесення, що утворені в попередньому циклі множення. При цьому перенесення, що отримані в попередньому циклі, повинні запам'ятовуватися до початку наступного циклу.

Приклад 4. Помножити числа А = 0, 10110 і В = 0, 11011, використовуючи метод множення з запам’ятовуванням проміжних перенесень.

Розв'язання. Для даних чисел маємо: =0; = 0, 10110; =0; = 0, 11011. Визначаємо знак добутку: =0 0=0.

Дії, що виконуються в процесі множення, наведені в табл. 3.17. Тут S - проміжна сума часткових добутків, P - проміжні перенесення.

Таблиця 5 - Приклад множення з запам’ятовуванням перенесень

Для остаточних кодів S і P виконується додавання з розповсюдженням перенесення:

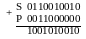
Відповідь: С= 0,1001010010.

До апаратних методів прискорення операції множення другого порядку відносяться матричні методи множення.

Коли множене і множник розташовані в регістрах машини, можна утворити відразу всі часткові добутки і здійснити їх одночасне додавання, використовуючи певну кількість суматорів. Узагальнена структура пристрою, що реалізує таке множення (рис. 3.6), містить: регістри РгА і РгВ, в яких зберігаються множене і множник, відповідно; блок елементів І, що забезпечує формування всіх часткових добутків; блок суматорів, у якому здійснюється одночасне додавання всіх часткових добутків. Матричні методи множення відрізняються саме організацією одночасного додавання.

Існує ряд методів множення, що засновані на додаванні груп часткових добутків з наступним об'єднанням сум разом з перенесеннями для одержання добутку. Наприклад, часткові добутки групуються по три і додаються із запам'ятовуванням перенесень за допомогою ланцюжка суматорів На кінці ланцюжка здійснюється додавання з розповсюдженням перенесень. Така роздільна обробка проміжних сум і перенесень вимагає так називаного "дерева суматорів" .

Реалізація матричних методів виконання операції множення вимагає більшої кількості апаратури, ніж методів послідовного аналізу розрядів або груп розрядів множника, і дає більший виграш у часі. Однак у зв'язку зі значним розвитком мікроелектроніки обмеження щодо кількості апаратури стають усе менш суворими, тому матричні методи широко застосовують на практиці.

Дерево суматорів

Лекція №4с. Ділення з відновленням залишку

Алгоритм ділення модулів чисел з відновленням остач полягає у виконанні таких дій.

1. Подвоїти модуль діленого .

2. Відняти від подвоєного модуля діленого модуль дільника. Одержана різниця є першою остачею.

3. Проаналізувати знак остачі R. Якщо , то черговому розряду частки присвоїти цифру 1 і перейти до п. 5; якщо ж R < 0, то черговому розряду частки присвоїти цифру 0.

4. Відновити остачу, додавши модуль дільника .

5. Подвоїти остачу.

6. Визначити чергову остачу, віднявши від попередньої остачі модуль дільника. Перейти до п. 3.

П. 3 - п. 6 виконувати до одержання всіх необхідних цифр частки.

За своїм характером операція ділення відноситься до операцій, що дають не завжди точний результат, тому ознакою закінчення операції ділення може бути досягнення заданої точності. Якщо в процесі ділення одержується остача R = 0, то операція зупиняється й у решту розрядів частки записується нуль. Звичайно формальною ознакою кінця операції ділення є одержання такої самої кількості розрядів у частці, яку мають операнди.

Подвоєння діленого та остачі практично виконується шляхом зсуву коду вліво на один розряд.

Приклад 1. Поділити число А = - 0, 10100 на число В = 0, 11011, використовуючи метод ділення з відновленням остач.

Розв'язання. Для даних чисел маємо: =1; = 0, 10100; =0; = 0, 11011. Визначаємо знак частки: =1 0=1. Віднімання будемо виконувати як додавання додаткових кодів, тому = 1,00101.

Усі дії, що виконуються в процесі ділення, наведені в табл. 1.

Таблиця .1 - Приклад ділення з відновленням остач

Відповідь: С= - 0, 10111.

З наведеного прикладу випливає, що цифри частки є інверсними значеннями знакових розрядів чергових остач. Треба також відзначити, що результат подвоєння іноді може бути > 1. Однак таке переповнення розрядної сітки усувається на наступному кроці алгоритму, оскільки після подвоєння завжди виконується віднімання.

Основні недоліки розглянутого методу ділення такі:

• аритмічність процесу ділення, яка обумовлена нерегулярністю виконання відновлення остачі, що призводить до ускладнення блоку керування діленням;

• відносно мала швидкість ділення, оскільки в середньому для половини кроків потрібно виконувати додаткове додавання, що забезпечує відновлення остач.

Для ритмізації процесу ділення можна виконувати фіктивну дію у тих випадках, коли відновлення остачі не потрібне, що призведе до збільшення часу виконання операції. Разом з тим, операцію можна спростити, якщо відмовитись від відновлення остач.