17.Динамічне рівняння руху матеріальної точки у координатній та натуральній формі (формі Ейлера)
Векторний
спосіб: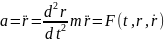
Координатний
спосіб: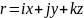
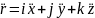
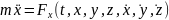
Система
рівнянь: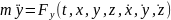
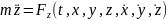
Натуральний
спосіб: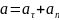
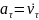
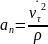ab
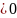
Система
рівнянь:
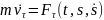
0=
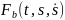
18.Зміст першої та другої задачі динаміки точки. Інтеграли рівнянь руху точки. Початкові умови.
Перша задача:
Задача визначення невідомих сил прикладання до точки за відомою масою та кінематичним законом руху точки.
Друга задача:
Задача визначення невідомого кінематичного руху за відомою масою та силою.
Перша (пряма) задача полягає у визначенні рівнодійної сили, якщо задано масу точки і її кінематичний закон руху, який спричиняється цією силою.
Який би спосіб (координатний чи натуральний) не застосовували, треба знайти проекції сили на осі, які дорівнюють добутку маси точки на відповідне прискорення . Тобто розв’язання першої задачі зводиться до відшукування прискорення, що неважко зробити, оскільки воно пов’язане з операцією диференціювання функцій. Знайдені проекції повністю визначають вектор рівнодійної, тобто модуль і його напрям.
При розв’язуванні другої (оберненої) задачі динаміки точки відомими є маса і сили, які прикладені до точки. Відомі також положення точки в певний момент часу t0 та її швидкість . Момент t0 називають початковим моментом часу, а положення точки та її швидкість у момент t0 - відповідно початковим положенням і початковою швидкістю.
За цими даними треба знайти закон руху точки. Друга задача динаміки значно складніша за першу, оскільки потребує інтегрування системи диференціальних рівнянь.
19.Класифікація в’язей за їх рівняннями. Рівняння Лагранжа першого роду.
Стаціонарна в’язь – це в’язь,у рівняння якої не входить час, а тільки координати точок.
Нестаціонарна в’язь – це в’язь, у рівняння якої входять час і координати точок.
Геометрична в’язь – це в’язь у рівнянні якої входять тільки координати точок і можливо час.
Кінематична в’язь – це в’язь, у рівняння якої входять проекції швидкостей точок і можливо час.
Голономні в’язі – це всі геометричні та кінематичні в’язі.
Утримувальна в’язь – це в’язь, при накладанні якої до кожного переміщення точки існує йому протилежне.
Неутримувальна – це в’язь, при накладанні якої до кожного переміщення точки не їснує йому протилежне.
Ідеальна в’язь – це в’язь, фізичні властивості якої дозволяють визначити напрям реакції наперед.
Перша задача Лагранжа на першу задачу динаміки:
невідомі: Fx, Fy, Fz, λрівнянь – 4.
На другу задачу динаміки:
Невідомі: x,y,z,λрівнянь – 4 .
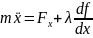
Система
рівнянь: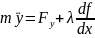
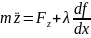
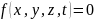
λ – множник Лагранжа;
20.Принцип Даламбера для матеріальної точки. Сила інерції та її фізичний зміст.
Принцип Даламбера:
векторна
сума:
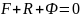
F – активна сила, R – реакція вязі, Ф – сила інерції
am=F+R
Рівністьназивають принципом Даламбера: активнісили і реакціїв’язей, прикладені до точки, “зрівноважуються” силою інерції.
Сила інерції дорівнює добутку маси на прискорення. Вона напрямлена в бік, протилежний прискоренню точки.
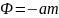
Це є головний вектор сил протидії, прикладених до зовнішніх тіл, одні з яких є джерелами активних сил, інші – в’язями, тому в природі існують реально тільки її складові, прикладені до різних тіл. Лише тоді, коли точка взаємодіє з одним тілом, головний вектор сил інерції фізично існує у вигляді однієї сили.