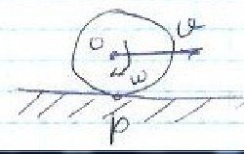
12.Теорема про додавання співнапрямленних обертальних рухів тіла навколо паралельних осей (з доведенням).

Теорема : сукупність двох обертальних рухів відносно паралельних осей є миттєвий обертальний рух навколо осі яка ділить відстань між складовими осями повороту обернено-пропорційні величинам кутових швидкостей внітрішним чином , якщо кутові швидкості спів напрямлені та зовнішнім чином якщо протилежні. Результуюча кутова швидкість дорівнює векторній сумі кутових швидкостей.

Перененосна швидкість :

V_e=w₁ * AM

Відносна швидкість:

V_r= w₂ * OM

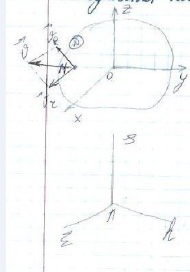
14.Теореми про додавання обертального та поступального рухів тіла (з доведенням). Кінематичний гвинт

Вектори кут. Шв. та швид.- перпенд икулярні

AEhs- нерухома СК, Axyz- рухома, V – швидк. СК Axyz, w- миттєва кут. Шв.

V (вект) - момент пари оберт.

V=00₁*w₁(вект), V=|00₁|*w₁

{w₁,w₂} – пари обертання, |00₁|=V/w – миттєвий оберт рух

Th- сукупність оберт та поступальних рухів при умові перпендикулярності веектора миттєвих кутових шв. і вектор швид. поступ. руху і миттєвим оберт. Рухом

{w1; V0} ~ { w(вектр), Р – МЦШ}

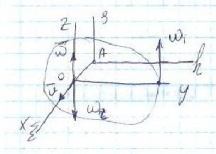
Векторна кутова швидкість та швидкість не перпендикулярна

AEhs- нерухома СК, Оxyz- рухома, Д – митт. Оберт рух

W не дорівнює V

VЄ Оxyz , V=V1+V2(вектр), V1 перпендикулярно V2

Кутміж w I V = a

V1=Vcosa, V2=Vsina

V1- шв. поступ руху

V2- момент пари обертання

|00₁|=v2/w1=Vsina/w – плече пари оберт.

Рух тіла яке є сукупн. Миттєвого оберт. Руху і миттєво – патун. Руху паралельно з веторами швидкостей назив. Кінемат. Гвинт . Таким чином у кожному випадку реаліз. Кінемат. Рух.

Теорема : Сукупність поступального руху та миттєво-оберт руху тіла з не перпендикулярним вектором швидкосте та кутов. Швидк. Є кінетичним гвинтом

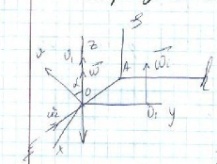
15.Додаванняпоступальнихрухів твердого тіла

Д-тіло, Оxyz – рухома СК, V2 – швидкість поступального руху тіла по СК Oxyz, V1 – рух СК OxyzyCK АЕh, Нехай т.М – довільна точка тіла Д , М- аналог. Рух у АEh, Vм=Ve+Vr(вектори) Ve-переноснийрух Vr- відносний рух Переносний рух М в Oxyz: Ve=V1 Відносний рух М в СК Oxyz: Vr = V2 Тоді Vм=V1+V2 М – довільна  будь-яка точка тіла Д має такуж швидкість, отже тіло Д здійснює поступальний рух. Теорема: сукупність двох поступальних рухів твердого тіла є постопульний рух швидкість якого дорівнює векторній сумі складових рухів

16. Закони Ньютона, принцип суперпозиції.

Динаміка – це розділ теоретичної мех. В якому вивчаються властивості механічних рухів з урахуванням факторів, що їх викликають. Такими факторами є сили.

Закони Ньютона виконуються в інерціальних системах відліку – система в якій тіло здійснює рівномірний прямолінійний рух.

1-ий закон Ньютона:

Ізольована матеріальна точка (тіло) зберігає стан спокою або рівномірного прямолінійного руху до того часу, поки дія інших тіл не виведе її з цього стану.

Ізольована матеріальна точка – це точка, взаємодію якої з іншими тілами можна знехтувати. Закон показує, що причиною зміни руху є взаємодія тіл. Взаємодія може бути контактна або через силові поля.

Сила – це фізична величина, яка характеризує міру механічної взаємодії.

2-ий закон Ньютона:

Зміна кількості руху матеріальної точки пропорційна прикладеної до неї сили і відбувається у бік дії сили.

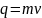– кількість руху мат точки.

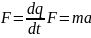– основний закон динаміки;

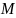аса – фізична величина, яка визначає вміст речовини у тілі і характеризує його інерційні та гравітаційні властивості.

3-ій закон Ньютона:

Усяка дія породжує рівну і протилежно напрямну протидію.

«Принцип суперпозиції» або закон незалежності дії сили:

Прискорення точки, яке викликається декількома силами дорівнює векторній сумі прискорень, кожне з яких викликається окремо взятою силою.