8.Регулярна процесія і кутове прискорення тіла, що має нерухому точку.

Регулярна процесія.Означення: регулярною процесієюназиваєтьсярухтіла, якиймаєнерухому точку, при якому кут нутаціїзалишаєтьсясталим, а кути процесії та власногообертання є лінійнимифункціями часу.

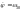
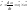
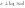
Визначимо вектор 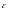інакше. Подаморухтіла як складний:

1. Переносний з

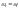навколо

2. Відносний - власнеобертання з кутом

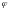
Абсолютнийрух:

У цьомувипадку

кутовашв. рух. СК.

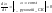
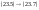
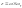
У випадкурегулярноїпроцесії

9.Способи визначення напрямних косинусів між осями систем координат.

Напрямні косинуси координатних осей

1. Спосіб: формули сферичної тригонометрії

Можна визначити за допомогою формулами сферичної тригонометрії або матрицями переходу.

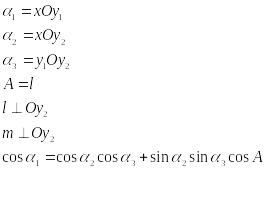А – лінійний кут двогранного кута при осі ОХ

Матриці переходу:

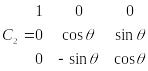
Перехід :

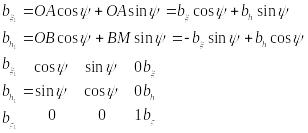
- матриця переходу від

Якщо ортим.

орти-

10.Теорема про додавання обертальних рухів тіла навколо перетин них осей (з доведенням).

Додаванняобертальнихрухів твердого тіланавколоперетинних осей.

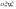-нерухома СК

-рухома

- миттєвий кут швидкостей

- миттєвийобертальнийрух з у СК

Довільнат.

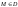
- складнийрух, двіскладові.

Відноснийрух

Переноснийрух

Оскільки т. - довільна, та за такою формулою визначитишв. будь-якої точки тіло - здійснюєобертальнийрух.

Теорема: сукупністьдвохобертальнихрухівтілавідносноперетинних осей є миттєвийобертальнийрух з кутовоюшвидкістю, яка збігається з діагоналлюпаралелограмапобудованого на кутовихшвидкостяхскладовихрухів.

11.Теорема про додавання обертальних рухів тіла які утворюють пару обертань (з доведенням).

Теорема 11 : Сукупність двох обертальних рухів тіла відносно перетинних осей є миттєвий обертальній рух з кутовою швидкістю, яка збігається з діагоналлю паралелограма побудованого на кутових швидкостях.

Пара обертань – це рух твердого тіла який є сукупністю двох обертальних рухів навколо паралельних осей з рівними за величиною і протилежно-напрямленими кутовіми швидкостями.

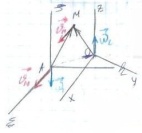
- Нерухома система координат

O_xyz – рухома, має ω₁ у рухомій СК

D – має кутову швидкість ω₂ у O_xyz

ω₁₌ -ω₂

Довільна т.М Є D.

М – складний рух/

V_M =V_e+V_r

Переносний рух відносно

V_e = ω₁ * АМ

Відносний рух у СК O_xyz

V_r = ω₂ * ОМ

Підставимо:

V_М = ω₁ * АМ + ω₂ * ОМ

ω₂ = - ω₁

V_М = ω₁ * (АМ – ОМ) = ω₁ * АО

V_М = ω₁ * АО = - АО * = ОА * ω₁

Аналогія:

ω₁ – F

V_М = ОА * ω₁

Момент пари обертань

V_М – М (F)

Оскільки т.М довільна, то за аналогією =>D – здійснює миттєво поступальний рух.

Т еорема. Тіло, яке приймає участь у парі обертань здійснює поступальний рух, швидкість якого дорівнює моменту пари обертань.

Додавання обертальних рухів навколо паралельних осей

- нерухома СК

O_xyz– рухома СК, ω₁ в нерухомій СК

D -ω₂в рухомій СК

ω₁ || ω₂ (ω₁ ,ω₂ – не пара обертань)

М – довільна точка, складний рух

V_M =V_e+V_r