
- •Екзаменаційні питання з Теоретичної механіки Кінематика
- •Динаміка
- •Виведення диференціального рівняння вільних коливань з урахуванням сил опору та його розв’язок у випадку великого опору. Визначення сталих інтегрування.
- •Виведення диференціального рівняння вільних коливань з урахуванням сил опору та його розв’язок у випадку кратних коренів характеристичного рівняння. Визначення сталих інтегрування.
- •Виведення диференціального рівняння вільних коливань з урахуванням сил опору та його розв’язок у випадку малого опору. Визначення сталих інтегрування.
- •Виведення диференціального рівняння змушених коливань з урахування сили опору. Визначення частинного розв’язку та його коефіцієнтів.
- •Кінематичний закон плоско паралельного руху тіла. Способи подання ппр тіла.
- •Теорема про розподіл швидкостей точок твердого тіла при плоскому русі (з доведенням).
- •Теорема про розподіл прискорень точок твердого тіла при плоскому русі (з доведенням).
- •8.Регулярна процесія і кутове прискорення тіла, що має нерухому точку.
- •9.Способи визначення напрямних косинусів між осями систем координат.
- •10.Теорема про додавання обертальних рухів тіла навколо перетин них осей (з доведенням).
- •11.Теорема про додавання обертальних рухів тіла які утворюють пару обертань (з доведенням).
- •12.Теорема про додавання співнапрямленних обертальних рухів тіла навколо паралельних осей (з доведенням).
- •14.Теореми про додавання обертального та поступального рухів тіла (з доведенням). Кінематичний гвинт
- •Векторна кутова швидкість та швидкість не перпендикулярна
- •15.Додаванняпоступальнихрухів твердого тіла
- •16. Закони Ньютона, принцип суперпозиції.
- •17.Динамічне рівняння руху матеріальної точки у координатній та натуральній формі (формі Ейлера)
- •18.Зміст першої та другої задачі динаміки точки. Інтеграли рівнянь руху точки. Початкові умови.
- •19.Класифікація в’язей за їх рівняннями. Рівняння Лагранжа першого роду.
- •20.Принцип Даламбера для матеріальної точки. Сила інерції та її фізичний зміст.
- •21.Принцип Даламбера для системи матеріальних точок. Рівняння кінетостатики.
- •28 . Випадок кратних коренів :
- •29. Малого опору :
- •33. Виведення диференціального
Закони Ньютона, принцип суперпозиції.
Динамічне рівняння руху матеріальної точки у координатній та натуральній формі (формі Ейлера)
Зміст першої та другої задачі динаміки точки. Інтеграли рівнянь руху точки. Початкові умови.
Класифікація в’язей за їх рівняннями. Рівняння Лагранжа першого роду.
Принцип Даламбера для матеріальної точки. Сила інерції та її фізичний зміст.
Принцип Даламбера для системи матеріальних точок. Рівняння кінетостатики.
Головний вектор та головний момент сил інерції у випадку поступального руху системи точок.
Визначення головного моменту сил інерції системи матеріальних точок у випадку обертального руху. Моменти інерції.
Динамічне рівняння відносного руху матеріальної точки. Ейлерові сили інерції. Умова відносного спокою. Принцип відносності Галілея.
Виведення диференціального рівняння вільних коливань точки без урахування сил опору, початкові умови. Характеристичне рівняння та загальний розв’язок диференціального рівняння.
Визначення сталих інтегрування розв’язку диференціального рівняння вільних коливань точки без урахування сил опору. Амплітуда, частота та період коливань.
Виведення диференціального рівняння вільних коливань з урахуванням сил опору та його розв’язок у випадку великого опору. Визначення сталих інтегрування.
Виведення диференціального рівняння вільних коливань з урахуванням сил опору та його розв’язок у випадку кратних коренів характеристичного рівняння. Визначення сталих інтегрування.
Виведення диференціального рівняння вільних коливань з урахуванням сил опору та його розв’язок у випадку малого опору. Визначення сталих інтегрування.
Залежність між амплітудами вільних коливань у випадку малого опору. Декремент коливань.
Виведення диференціального рівняння змушених коливань без урахування сили опору. Визначення частинного розв’язку у нерезонансному випадку та його коефіцієнтів.
Виведення диференціального рівняння змушених коливань без урахування сили опору. Визначення частинного розв’язку у резонансному випадку та його коефіцієнтів.
Виведення диференціального рівняння змушених коливань з урахування сили опору. Визначення частинного розв’язку та його коефіцієнтів.
Визначити залежність амплітуди (або коефіцієнта динамічності) змушених коливань з урахуванням сили опору від частоти збурю вальної сили.
|
|
|
|
|
1 |
0 |
0 |
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
0 |
0 |
1 |
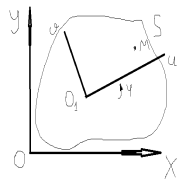
Кінематичний закон плоско паралельного руху тіла. Способи подання ппр тіла.
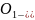 довільний
полюс
довільний
полюс
uVрухома
(X0,Y0)-нерухомий полюс
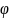 –кут
повороту
–кут
повороту
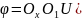 (18.1)
(18.1)
 Кінем
закон ПП рухуТТ
Кінем
закон ПП рухуТТ
Висновки
Положеннятіла при ПП рухувизначається 3-ма параметрами
ПП рухтіламожна подати як сукупність 2 рухів: поступальногоруху разом з довільновибраним полюсом та обертрухомнавколоосіщо проходить через цей полюс
З (18,1) випливає, щокінемхар-ми обертруху не залежитьвідвибору полюса тому вектор кут швможе бути
Теорема про розподіл швидкостей точок твердого тіла при плоскому русі (з доведенням).
Розподілшвидкостейточоктіла при ПП русі
Теорема: шв будь-якої точки тіла яке здійсн ПП рух дор векторнійсумішвидкостідовільновибраного полюса та швидкостіобертруху точки навколоцього полюсу
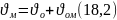
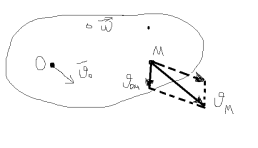
Доведення А-нерухомий полюс
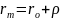 (18.3)
(18.3)
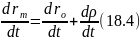
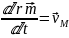 за
озн шв-ті точки
за
озн шв-ті точки
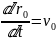
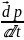 -
швидкість М відносно О
-
швидкість М відносно О
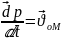 М
до О – оберт рух
М
до О – оберт рух
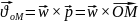
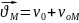 ;
;
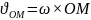 (18,5)
(18,5)
Теорема про розподіл прискорень точок твердого тіла при плоскому русі (з доведенням).
Розподіл прискорень точок плоскої
Теорема: Прискорення будь якої точки тіла яке здійснює плоско паралельний рух рух дорівнює векторній сумі прискорення довільно вибраного полюса та прискорення оберт руху навколо цього полюса
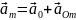
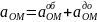 (19,1)
(19,1)
Доведення: О – полюс
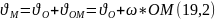
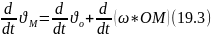
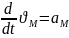
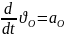
2 доданок
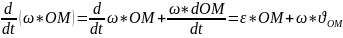
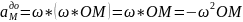
Т2: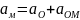
Доведення
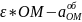 обертальнеприскорення
М відносно О (19,4)
обертальнеприскорення
М відносно О (19,4)
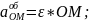
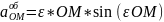

.6.Теорема Ейлера. Кути Ейлера. Ріняння руху твердого тіла з нерухомою точкою
Визначимо закон руху тіла навколо нерухомої точки. Зв’яжемо незмінно з тілом систему координат (рис. 33) з початком у нерухомій точці О. Положення цієї системи визначатимемо відносно нерухомої системи координат Oxyzз початком у тій самій точці.
Припустимо, що в початковий момент часу осі цих систем координат збігаються. Положення системи однозначно визначає положення тіла. Доведемо теорему про переміщення тіла, що має нерухому точку.
Теорема Ейлера. Довільне переміщення тіла навколо нерухомої точки можна здійснити трьома послідовними поворотами тіла навколо трьох особливим способом вибраних осей, що проходять через нерухому точку.
Перший поворот на кут здійснюємо навколо осі Oz. Вісь займає проміжне положення ON. Другий поворот на кут здійснюємо навколо осі ON, яку називають лінією вузлів. Після цього повороту площина суміститься із своїм кінцевим положенням, осі і займуть проміжні положення, а вісь – кінцеве. Третій поворот робимо навколо цієї осі на кут . Рухома система координат займає кінцеве положення.
Кути поворотів і (кути Ейлера) визначають положення тіла: – кут прецесії; – кут нутації; – кут власного обертання.
Кожному моменту часу відповідають певні значення кутів Ейлера. Отже, кути Ейлера є функціями часу:
З доведеної леми (підрозд. Додавання обертальних рухів тіла навколо осей, що перетинаються) можна зробити логічний висновок: миттєва кутова швидкість тіла, що рухається навколо нерухомої точки, дорівнює векторній сумі кутових швидкостей прецесії , нутації і власного обертання .
Модуль вектора можна знайти, якщо визначити його проекції на осі ортогональної (рухомої або нерухомої) системи координат. Проекції вектора на осі координат визначаються кінематичними формулами Ейлера. Вектор кутового прискорення напрямлений по дотичній до годографа вектора кутової швидкості .
Зауважимо, що на практиці часто зустрічається випадок руху тіла навколо нерухомої точки, коли кут нутації залишається незмінним, а кутові швидкості прецесії і власного обертання – сталі. Цей випадок руху тіла навколо нерухомої точки називають регулярною прецесією.
