19) Способ вращения вокруг линии уровня

Этот способ применяется в основном для решения задачи преобразования плоскости общего положения в плоскость уровня. Суть способа заключается в том, что плоскость общего положения, поворачивается вокруг прямой уровня до состояния, параллельного горизонтальной плоскости проекций П1 либо фронтальной П2.

Рассмотрим поворот точки А вокруг горизонтали a до уровня горизонтали. Точка А движется по дуге окружности радиуса R с центром в точке O, принадлежащей горизонтали a. Радиус R является гипотенузой прямоугольного треугольника А0А1O, где один катет А1О - горизонтальная проекция радиуса вращения, другой - равен Dz - расстояние между точкой A и прямой a по вертикали. А' - новое положение точки А.

Алгоритм графических построений:

Через А1 проводим горизонтальную проекцию дуги по которой поворачивается точка А. Это будет прямая, перпендикулярная прямой a1;

На пересечении прямой a и проекции дуги отмечаем точку O1;

Строим прямоугольный треугольник A1A0O1. Попутно мы решили задачу нахождения расстояния между прямой и точкой. Отрезок A0O1 - расстояние от точки A до прямой a;

Обратите внимание, на то, что построения, выполняемые на верхнем демонстрационном чертеже выполняются в вертикальной плоскости, а на ортогональном чертеже мы делаем те же построения, только в горизонтальной плоскости. На результат построений такой прием не влияет;

Проводим дугу A0A1' с центром в точке O1. А1' - новая проекция точки А;

Подняв от A1' линию проекционной связи до пересечения с a2 находим A2'.

20) Сущность способа совмещения

Эффективным приёмом, упрощающим решение ряда задач, связанных с определением метрических характеристик плоских фигур, с построением в плоскости общего положения фигуры заданной формы и размеров, является поворот плоскости вокруг её следа до совмещения с плоскостью проекций. Этот способ преобразования чертежа, являющийся частным случаем вращения плоскости вокруг линии уровня, известен в начертательной геометрии как способ совмещения.

При совмещении за ось вращения принимается её горизонтальный или фронтальный след - нулевые горизонталь или фронталь. В результате поворота плоскости она совпадает (совмещается) с плоскостью проекций П1, если вращение осуществляется вокруг горизонтального следа плоскости, либо с П2 при вращении вокруг её фронтального следа.

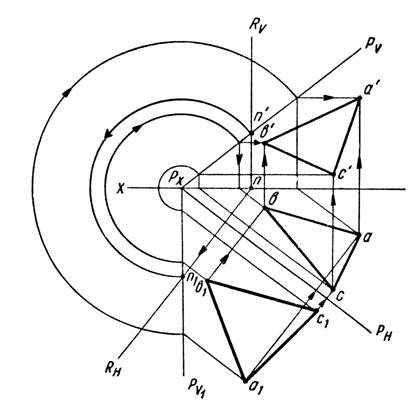
На рисунке 1 показано совмещение плоскости общего положения Р с горизонтальной плоскостью проекций П1. Поворот произведён вокруг горизонтального следа Рh, в направлении от фронтальной плоскости проекций к зрителю.

В положении совмещения с плоскостью П1 на плоскости Р окажутся две пересекающиеся прямые – след Рh и прямая Рv/, которая представляет собой след Рv, совмещённый с плоскостью П1.

След Рh, как ось вращения, не меняет своего положения, точка пересечения следов Рх - точка схода следов, также не меняет своего положения. Поэтому для нахождения совмещённого положения плоскости достаточно найти совмещённое положение ещё одной точки (кроме Рх), принадлежащей фронтальному следу Рv – точки N. Эта точка опишет дугу окружности в пл. Q, перпендикулярной к оси вращения, центр этой дуги лежит в точке О – пересечения плоскости Q со следом Рh. Описывая из точки О дугу радиусом ОN в плоскости Q, мы получаем в пересечении этой дуги с Qh точку N′ на плоскости П1.

Проведя через Рх и N′ прямую, получим Рv′. Так как отрезок РxN не изменяет своей величины при вращении плоскости, то, очевидно, точку N можно получить в пересечении Оh с дугой, описанной в пл. П1 из Рх радиусом РхN.

На рисунке 2 это же построение выполнено на эпюре.

Длину радиуса вращения R точки N можно определить и методом прямоугольного треугольника (см. рисунок 3) – гипотенуза ОN.

При решении некоторых задач заданная плоскость, из совмещенного положения возвращается в исходное, то есть, производится подъем в пространство, расположенных на плоскости заданных форм.

Графические построения, которые надо выполнить, чтобы поднять плоскость в пространство, аналогичны построениям, выполняемым при совмещении плоскости с плоскостью проекции, только они выполняются в обратной последовательности.

Проекции точки, принадлежащей плоскости, при совмещении строятся с помощью линий уровня, проходящих через заданную точку.