16) Способ вращения

Способ вращения геометрической фигуры вокруг некоторой оси состоит в том, что фигура вращается вокруг оси до требуемого положения относительно заданной неподвижной системы плоскостей проекций.

В качестве оси вращения может быть взята любая прямая. В практике же преобразования комплексного чертежа широкое распространение получило вращение вокруг проецирующих прямых и линий уровня.

Рис. 6.1.

При вращении некоторой точки вокруг оси она описывает окружность, расположенную в плоскости, перпендикулярной оси вращения. На рис.6.1 рассмотрено вращение точки А вокруг горизонтально проецирующей оси. Плоскость вращения D параллельна плоскости П1 и на фронтальной проекции изображается следом D2. Горизонтальная проекция О1 центра вращения О совпадает с проекцией M1N1 оси, а горизонтальная проекция О1А1 радиуса вращения является его натуральной величиной. Вращаясь вокруг оси, точка А перемещается по окружности, которая на А1 проецируется в окружность, а на П2 - в отрезок прямой, параллельный оси х. На рис.6.1 поворот произведен на угол j против часовой стрелки так, чтобы в новом положении точки радиус вращения был параллелен плоскости П2.

Если точку вращать вокруг оси, перпендикулярной плоскости П2, то ее фронтальная проекция будет перемещаться по окружности, а горизонтальная - параллельно оси х.

Вращение вокруг проецирующей прямой применяют при решении задачи на определение натуральной величины отрезка прямой (рис.6.2). Ось вращения выбирают так, чтобы она проходила через одну из крайних точек отрезка, например, через точку В. Тогда при повороте точки А на угол j в положение А отрезок АВ перемещается в положение АВ, параллельное плоскости П2. В этом случае отрезок будет проецироваться на П2 в натуральную величину ( ½В 2А2 ½= ½ВА ½). Одновременно в натуральную величину будет проецироваться угол а наклона отрезка АВ к плоскости П1.

Рис. 6.2.

Натуральную величину плоской фигуры удобнее находить с помощью вращения вокруг прямой уровня. Путем такого вращения плоскость, которой принадлежит рассматриваемая фигура, поворачивают в положение, параллельное плоскости проекций. При таком положении плоскости любая принадлежащая ей фигура будет проецироваться в натуральную величину.

Вращая плоскость вокруг горизонтали, можно перевести ее в положение, параллельное плоскости П1. Вращение плоскости вокруг фронтали позволяет перевестиее в положение, параллельное плоскости П2.

На рис.6.3 рассмотрено нахождение натуральной величины треугольника АВС при помощи вращения его вокруг горизонтали. Каждая точка плоскости треугольника АВС при вращении перемещается по окружности, перпендикулярной оси вращения. Так, точка В перемещается по окружности, плоскость D которой перпендикулярна горизонтали. Центр окружности О находится на оси вращения, а величина радиуса равна расстоянию от точки до оси вращения. Так как точка В вращается вокруг горизонтали, то окружность проецируется на П1 в отрезок прямой, перпендикулярный горизонтали, а на П2 - в эллипс, который можно не строить.

Рис. 6.3.

На рис.6.3 видно, что и на П1, и на П2 радиус вращения проецируется с искажением. Натуральную величину радиуса находим методом прямоугольного треугольника (см. свойство ортогонального проецирования). Для этого принимаем горизонтальную проекцию О1В1 за катет прямоугольного треугольника. Второй катет должен быть равен разности координат Z концов отрезка OB (ZВ - Z0). Гипотенуза треугольника О1В1В1' (О1В1') равна R. После поворота плоскость треугольника будет параллельна П1. Следовательно, 0В спроецируется на П1 в натуральную величину. Горизонтальную проекцию нового, после поворота, положения точки В (В1') находим на пересечении дуги окружности, проведенной из горизонтальной проекции центра вращения О1, радиусом, равным О1В1, с горизонтальной проекцией плоскости A (А1).

Точка С также перемещается по окружности, плоскость которой Г перпендикулярна горизонтали. Точка 1 находится на горизонтали, поэтому при вращении не перемещается. Так как точки В, 1 и С находятся на одной прямой, то горизонтальную проекцию нового, после поворота, положения точки С найдем на пересечении прямой, проведенной через В1 и 11, с горизонтальной проекцией плоскости Г (Г1).

17) Вращение точки вокруг оси, перпендикулярной плоскости проекций. Дана ось i, перпендикулярная к плоскости проекций П1, и точка А, вращающаяся вокруг нее в плоскости β, параллельной плоскости П1 и одновременно перпендикулярной к оси вращения i (фиг.261).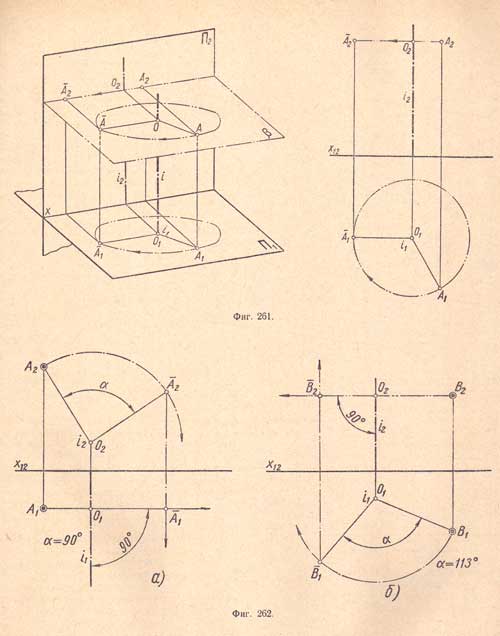

18) Метод вращения вокруг линии уровня

Суть метода заключается в том, что осью вращения выбирается одна из линий уровня - горизонталь или фронталь плоскости или плоской фигуры. Таким образом, плоскость как бы поворачивается вокруг некоторой оси, принадлежащей этой плоскости, до положения, при которой эта плоскость становится параллельной одной из плоскостей проекций.

Например, повернем плоский угол, образованный пересекающимися прямыми а и b (рис. 9.6).

Для решения поставленной задачи проводят в плоскости угла горизонталь h и используют ее как ось вращения, вокруг которой будут вращаться прямые а и b и вершина К. Все точки вращаются в плоскостях, перпендикулярных к горизонтали, при этом точки 1 и 2 остаются неподвижными, а точка К вращается вокруг горизонтали. Из горизонтальной проекции К1 точки К проводят линию, перпендикулярную к оси вращения h1. Отрезок K1O1- горизонтальная проекция радиуса вращения точки К. Натуральную величину этого радиуса находят методом построения прямоугольного треугольника.

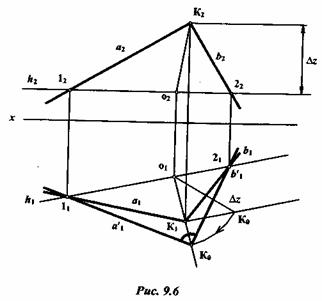
На продолжении прямой O1K1 откладывают гипотенузу O1K0 и получают совмещенное положение К0 Соединив точки 11 и 21 с точкой К0, получают натуральную величину угла при вершине К.

Этим способом находится натуральная величина любой плоской фигуры, плоского угла.

В техническом рисовании направление лучей света выбирается условно, но так, чтобы источник света находился сверху, слева и сзади рисующего, а световые лучи при этом составляют угол наклона к горизонту 45°. Таким образом, характерной особенностью технического рисунка является условное направление лучей света. Независимо от того, как рисуется предмет - с натуры или по чертежу, свет всегда находится слева, а тень - справа.