12) Определение видимости на эпюрах.

При пересечении прямой с плоскостью для улучшения наглядности чертежа для показа видимых линий применяют сплошные основные линии, для невидимых линий - штриховые. При показе видимости линий на эпюре предполагается, что:

Плоскости и поверхности непрозрачные.

Наблюдатель всегда находится в первой четверти или первой октанте.

Луч зрения от наблюдателя перпендикулярен к той или иной плоскости проекций (по отношению к которой определяется видимость).

Конкурирующие точки

Две точки, лежащие на проецирующей прямой, называются конкурирующими. С помощью конкурирующих точек можно определять взаимную видимость геометрических фигур на эпюре Монжа.

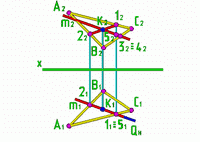
Рассмотрим две пары конкурирующих точек АВ ^p1 и CD ^p2. Видимость фигур на эпюре Монжа определяют для каждой проекции отдельно и считают, что направление взгляда на ту или иную плоскость проекций совпадает с направлением проецирования. При этом взгляд зрителя находится перед плоскостью p1 при решении вопроса о видимости в первом поле и над плоскостью p2 при определении видимости во втором поле. В любом случае видимой считают ту точку, которая находится ближе к наблюдателю. На чертеже в исходном пространстве показаны способы определения видимости в первом поле конкурирующих точек А и B и во втором поле конкурирующих точек C и D. В первом случае точка B расположена ближе к наблюдателю (V), поэтому точка B будет видима, а точка А – невидима.

Такой же результат видимости будет и в том случае, если вместо точек А и B воспользуемся их вторыми проекциями А2 и В2 и наблюдатель будет смотреть в направлении S1 (V).

Аналогично определяют видимость точек А и B на модели. Для этого во втором поле смотрят на точки А2 и В2 в направлении S1 (V). Точка В2 ближе к зрителю, поэтому в первом поле В1 будет видима.

При определении видимости точек C2 и D2 во втором поле смотрят на их первые проекции C1 и D1 по направлению S2 (W). Точка C1 расположена ближе к зрителю, поэтому ее вторая проекция – C2 будет видима.

13) Проецирующей является такая плоскость s, которая заключает в себе (которой принадлежат) проецирующие прямые на плоскость Пi, т.е. s Пi. В ортогональной системе проецирующая прямая для одной плоскости проекций всегда является прямой уровня (параллельной) для другой плоскости проекций. Таким образом, если в плоскости общего положения s провести прямую уровня (горизонталь, фронталь или профильную прямую) и ввести дополнительную плоскость проекций П3 такую, что П3 перпендикулярна прямой уровня, то плоскость s будет перпендикулярна П3 (s П3) и, соответственно, s проецируется на П3 в виде прямой. Это позволит нам определить углы ее наклона к плоскостям проекций П1 (угол a), П2 (угол b), П3 (угол g).

Рассмотрим графическое решение данной задачи на примере плоскости s (АВС), показанной на (рис. 5.6). Если требуется спроецировать плоскость s в прямую и одновременно определить угол a, то будем вводить дополнительную плоскость проекций П3 таким образом, чтобы она была перпендикулярна прямой частного положения параллельной П1, т.е. горизонтали (h = MN).

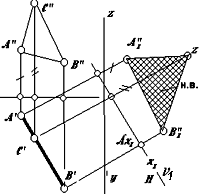
Алгоритм графических построений:

Проводим проекцию M2N2 горизонтали, принадлежащей плоскости АВС: h2 = M2N2 || П1/П2;

Проводим линии проекционной связи и находим проекцию M1N1 этой прямой на П1;

Проводим ось проекций П1/П3 перпендикулярно M1N1 = h1;

Проводим линии проекционной связи из точек первой проекции треугольника ABC перпендикулярно оси П1/П3;

Откладываем на них от оси П1/П3 расстояния равные расстояниям от А2, B2, C2, M2 и N2 до оси П1/П2;

Соединяем точки и получаем проекцию плоскости ABC на П3. Угол a наклона А3, B3, C3 к оси П1/П3 равен углу наклона плоскости треугольника ABC к П1.

К решению подобной задачи сводится решение других задач на определение углов наклона плоскости к плоскостям проекций, расстояний от точки до плоскости, между параллельными плоскостями, плоскостью и параллельной ей прямой и т.п.

14) Пересечение прямой с плоскостью.

Если прямая не лежит в плоскости и не параллельна ей, она пересекает плоскость.

Задача на определение точки пересечения прямой с плоскостью сводится к следующему:

1) проведению вспомогательной плоскости (Вспомогательную плоскость рекомендуется выбирать такую, которая даст наиболее простое графическое решение задачи) через данную прямую;

2) нахождению линии пересечения вспомогательной плоскости с данной плоскостью;

3) определению точки пересечения данной прямой с линией пересечения плоскостей, а следовательно, с данной плоскостью.

Пересечение прямой с проектирующей плоскостью.

Пример 1. На (фиг.250,а) даны плоскость δ (δ1) и прямая АВ (А1В1 и А2В2); требуется определить точку их пересечения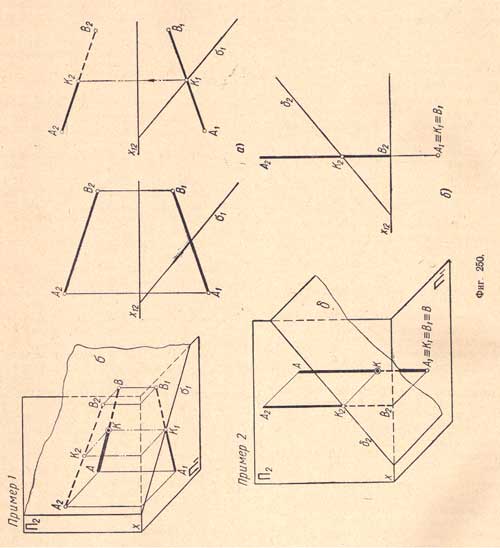

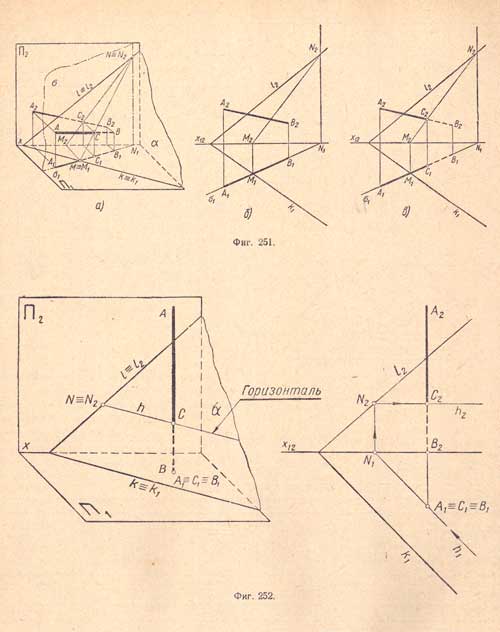
В этом случае нет надобности прибегать к вспомогательной плоскости, так как данная плоскость δ - горизонтально - проектирующая. По свойству проектирующих плоскостей горизонтальная проекция точки пересечения, лежащая в плоскости δ, сливается с горизонтальной проекцией δ1.

Поэтому точка К1 пересечения горизонтальной проекции А1В1 прямой АВ с горизонтальной проекцией δ1 есть горизонтальная проекция точки пересечения К; фронтальная проекция К2 определяется путем проведения вертикальной линии связи до пересечения ее с фронтальной проекцией А2В2.

Пример 2. На (фиг.250,б) приведен пример пересечения прямой АВ с фронтально - проектирующей плоскостью δ.

Пересечение прямой с плоскостью общего положения.

Пример 1. Даны: плоскость общего положения а и прямая общего положения АВ (А1В1 А2В2); требуется найти точку их пересечения (фиг.251,а).

Проводим через прямую АВ какую - либо вспомогательную плоскость, например горизонтально - проектирующую плоскость δ (δ1), как показано на (фиг.251,б); она пересечет плоскость a по прямой NM (N1M1, N2М2), которая, в свою очередь, пересечет прямую АВ (А1В1 А2В2) в точке С (С1С2), что видно на (фиг.251,в). Точка С есть точка пересечения прямой АВ с плоскостью а.