3.Принадлежность точки прямой

А. Принадлежность точки линии.

Основное положение в этом случае таково:

точка принадлежит прямой, если ее проекции принад­лежат одноименным проекциям этой прямой (рис. 17).

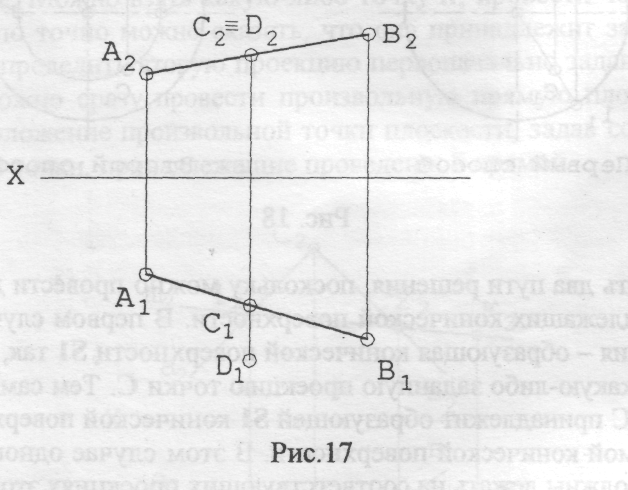
(На рис. 17 точка С принадлежит прямой АВ, а точка D - АВ не принадлежит).

9.. Условия принадлежности прямой линии плоскости

Прямая принадлежит плоскости, если она проходит через две точки, принадлежащие этой плоскости или через одну точку этой плоскости, параллельно прямой, лежащей в этой плоскости.

Задача

Провести прямую, принадлежащую данной плоскости. Рассмотрим пример на основе применения определения, когда плоскость задана разными способами (табл. 5.5).

Таблица 5.5

Условие	Комплексный чертеж
Плоскость задана тремя точками A, B, C. Решение: провести прямую m через любые две точки (в частности, A и B)

Плоскость задана точкой А и прямой а. Решение: 1) на прямой а выбираем любую точку L (L2); строим L1 2) через А и L проводим прямую b
Плоскость задана двумя пересекающимися прямыми: а  b = K. Решение: 1) выбираем произвольные точки на прямой a L(L1L2), и на прямой b – M (M1M2). 2) проводим прямую c через эти точки
Плоскость задана двумя параллельными прямыми а || b. Решение: 1) выбираем на прямых по одной произвольной точке K a и L  b; 2) через одноименные проекции K и L проводим прямую с
Плоскость задана плоской фигурой. Решение: 1) на любых сторонах треугольника выбираем произвольные точки K и L; 2) через одноименные проекции проводим проекции прямой а

9.Принадлежность точки плоскости

Точка принадлежит плоскости, если она принадлежит какой-либо прямой, лежащей в этой плоскости (рис. 5.7).

Рис. 5.7

Точка D принадлежит плоскости  ( АВС), так как D₁  А₁1₁; D₂  А₂1₂, а прямая А1 принадлежит плоскости  ( АВС) в соответствии с § 4.

Или

§ 7. Принадлежность точки прямой

Рис. 3.4

Точка принадлежит прямой, если их одноименные проекции совпадают (рис. 3.4). Точка С принадлежит отрезку АВ, так как С2 принадлежит фронтальной проекции отрезка, а С1 – горизонтальной проекции отрезка.

Задача № 1

Определить, принадлежит ли точка С отрезку прямой АВ.

12 . Пересечение двух плоскостей

Две плоскости пересекаются по прямой линии. Для построения линии их пересечения необходимо найти две точки, принадлежащие этой линии. Задача упрощается, если одна из пересекающихся плоскостей занимает частное положение. В этом случае ее вырожденная проекция включает в себя проекцию линии пересечения плоскостей.

На рис. 122 приведен комплексный чертеж двух пересекающихся плоскостей £ и 0, причем плоскость Sum частного положения — фронтально проецирующая. Она пересекает линии АВ и АС плоскости 0, данной треугольниками ABC — плоскости общего положения. Точки пересечения 1 и 2 и определяют линию пересечения плоскостей. Соединив их, получаем искомую линию: a(1, 2) = Sum^Q.

Линию пересечения двух плоскостей, занимающих общее положение, можно построить в исходной системе плоскостей проекции. Для этого дважды решают задачу на построение прямой одной плоскости со второй плоскостью. Задачу можно решать в новой системе плоскостей проекции, построив изображение одной из пересекающихся плоскостей как плоскости проецирующей.

На рис. 123, а построена линия пересечения двух треугольников ABC и DEF путем построения точки М пересечения линии АВ с плоскостью DEF и точки N пересечения линии EF с плоскостью АВС:

1) АВ ~ Sum¹(Sum¹_|_П₂), Sum¹ ^DEF=l -2(1₂—2₂; 1₁—2₁), 1₁—2₁ ^ А₁B₁ = М_1, M₁,M₂ || А₁A₂,М₁М₂ ^ А₂В₂ = М₂,М(М,М₂);

Рис. 122

Рис. 123

2) EF ~ Sum²(Sum²_|_П₂), Sum² ^ ABC = 3—4(3₂—4₂; 3₁—4₁),3₁-4₁ ^ E₁F₁= = N₁, N₁N₂ || A₁,A₂; N₁N₂^ E₂F₂ = N₂; N(N₁,N₂);

3) M₁ U N₁, = M₁N₁, M₂ U N₂ = M₂N₂;

4) ABC^DEF = MN.

После построения определяют видимость пересекающихся плоскостей. На фронтальной плоскости она определена с помощью фронтально конкурирующих точек 1 и 5. Для определения видимости на горизонтальной плоскости проекций использованы горизонтально конкурирующие точки 6 и 7.

На рис. 123, б эта же линия пересечения построена с помощью дополнительных проекций данных плоскостей на плоскости П₄, относительно которой плоскость DEF занимает проецирующее положение. Дополнительные проекции построены из условия, что горизонталь h € DEF проецируется в точку на плоскости П₄ _|_ h. Новые линии связи проведены .через незаменяемые горизонтальные проекции точек А,

В, С, D, E, F параллельно h₁, а новая ось проекций П₁/П₄ _|_ h₁. Замеренные на плоскости П₂ высоты точек определили их проекции на плоскости П₄.

A₄B₄C₄^ D₄E₄F₄ = M₄K₄, так как А₄В₄ ^ D₄E₄F₄ = М₄ и В₄С₄ ^ D₄E₄F₄ = = К₄. По направлению новых линий связи определяем горизонтальную проекцию линии МК (М₁К₁). Отмечаем точку пересечения стороны EF c линией МК: E₁F₁ ^ M₁K₁ = N₁. Точки отрезка NK не имеют общих точек с плоскостью DEF.

Пересекающиеся плоскости в частном случае могут быть перпендикулярными. Для выявления случаев перпендикулярности надо помнить, что если две плоскости взаимно перпендикулярны, то одна из них проходит через перпендикуляр к другой плоскости. На рис. 122 дан комплексный чертеж взаимно перпендикулярных пересекающихся плоскостей: одна фронтально проецирующая Sum (Sum₂), а вторая — общего положения (ABC) — содержит в себе перпендикуляр АВ к плоскости Sum(AB||П₂; A₂B₂Sum₂).

Две плоскости в общем случае могут пересекаться в бесконечности. Тогда имеет место параллельность этих плоскостей. При выявлении этого случая следует учитывать, что у параллельных плоскостей две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости. На рис. 91 плоскость S параллельна плоскости Sum₂, так как а || с, b || d.

Или http://www.t-agency.ru/geom/part3/part3-5-1.html

13.

3.5  Пересечение двух плоскостей
	3.5.1  Пересечение плоскостей общего и частного положения
	Пусть нам дана плоскость частного положения    П1 и плоскость общего положения, заданная треугольником АВС. Требуется построить линию пересечения плоскости  с плоскостью АВС. Нажмите на картинку для просмотра...  Рассмотрим сначала пространственную модель, на которой даны плоскость , плоскость АВС и плоскость проекций П1. Спроецируем плоскости  и ABC на П1. Плоскость общего положения АВС проецируется на плоскость П1 в виде треугольника А1В1С1, а плоскость частного положения  - в виде прямой 1. На плоскости П1 прямая 1 и АВСпересекаются в точках K1 (K1 принадлежит А1В1) и N1 (N1принадлежит А1C1). Если через точки K1 и N1 провести проецирующие прямые до пересечения с плоскостью АВС, то получатся две точки K (K принадлежит АВ) и N (Nпринадлежит АC). Соединив точки K и N, мы получим прямую KN. Прямая KN - линия пересечения плоскости  с плоскостью АВС. Нажмите на картинку для просмотра...  Теперь обратимся к комплексному чертежу. K1 принадлежит1 , следовательно K принадлежит . K1 принадлежит A1B1, аK2 принадлежит A2B2, следовательно K принадлежит AB. Из этих утверждений следует, что K - точка пересечения прямой АВ с плоскостью . Возьмем точку N и проделаем те же действия. Теперь рассмотрим ABС (заданный пересекающимися прямыми АВ, АС). КN - линия пересечения плоскости ABС с плоскостью .