- •2Точка в системе 1, 2, 3
- •Частные случаи пересечения прямой с плоскостью
- •20.Расстояние между двумя параллельными прямыми – определение.
- •27.Построение линии пересечения пирамиды с прямой призмой
- •28.Поверхности вращения
- •29. Точка и линия на поверхности
- •3.Принадлежность точки прямой
- •9.. Условия принадлежности прямой линии плоскости
- •9.Принадлежность точки плоскости
- •§ 7. Принадлежность точки прямой
- •12 . Пересечение двух плоскостей
- •13. Построение линии пересечения двух плоскостей.
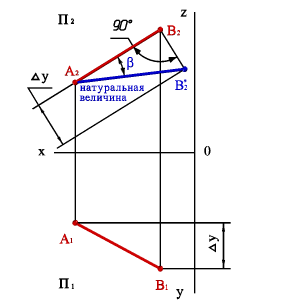
- •16.Способ прямоугольного треугольника. Определение натуральной величины отрезка прямой линии и углов наклона прямой к плоскостям проекций
- •§ 6. Определение натуральной величины отрезка прямой общего положения
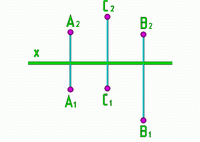
4.Положение прямой относительно плоскостей проекций. Следы прямой В зависимости от положения прямой по отношению к плоскостям проекций она может занимать как общее, так и частные положения. 1. Прямая не параллельная ни одной плоскости проекций называется прямой общего положения (рис.3.1).

Рисунок 3.1 Прямая общего положения2. Прямые параллельные плоскостям проекций, занимают частное положение в пространстве и называются прямыми уровня. В зависимости от того, какой плоскости проекций параллельна заданная прямая, различают:2.1. Прямые параллельные горизонтальной плоскости проекций называются горизонтальными или горизонталями (рис.3.2).

Рисунок 3.2 Горизонтальная прямая 2.2. Прямые параллельные фронтальной плоскости проекций называются фронтальными илифронталями(рис.3.3).

Рисунок 3.3 Фронтальная прямая 2.3. Прямые параллельные профильной плоскости проекций называются профильными (рис. 3.4).
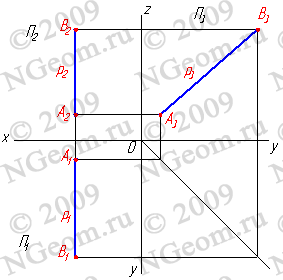
Рисунок 3.4 Профильная прямая 3. Прямые, перпендикулярные плоскостям проекций, называются проецирующими. Прямая перпендикулярная одной плоскости проекций, параллельна двум другим. В зависимости от того, какой плоскости проекций перпендикулярна исследуемая прямая, различают: 3.1. Фронтально-проецирующая прямая - АВ (рис. 3.5).

3.2. Профильно проецирующая прямая - АВ (рис.3.6).

3.3. Горизонтально-проецирующая прямая - АВ (рис.3.7).

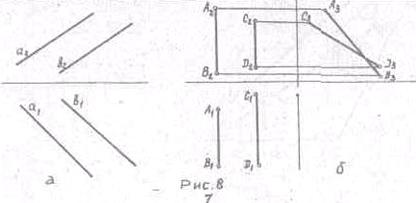
5.Взаимное положение двух прямых Параллельные прямые. Проекции двух параллельных прямых параллельны между собой (Рис.8 а)
Для профильных прямых для определения параллельности прямых, необходимо, чтобы все три проекции прямых были параллельны, т.к. две проекции профильной прямой не определяют параллельность. (Рис.8 б)
Пересекающиеся прямые. Если прямые линии пересекаются, то п. одноименные проекции пересекаются между собой в точке, которая является проекцией точкой пересечения этих прямых.
Необходимым и достаточным условием является лишь то, чтобы точки пересечения одноименных проекций находились на одном перпендикуляре к соответствующей оси проекций (Рис.9.)

Рис.9 Скрещивающиеся прямые. Скрещивающиеся прямые линии не пересекаются и не параллельны между собой. Хотя одноименные проекции и пересекаются между собой, но точки их пересечения не могут быть соединены линией связи, т.е. эти прямые не пересекаются между собой Точки пересечения одноименных проекции скрещивающихся прямых представляют собой проекции двух точек, из которых одна принадлежит первой, а другая - второй из этих скрещивающихся прямых. (Рис. 10).

2Точка в системе 1, 2, 3
Построение проекций некоторой точки А, расположенной в I октанте, на три взаимно перпендикулярные плоскости 1, 2, 3 показано на рис. 2.27. Используя совмещение плоскостей проекций с плоскостью 2 и применяя способ вращения плоскостей, получаем комплексный чертеж точки А (рис. 2.28):
АА1 1; АА 2 2; АА 3 3,
где А3 – профильная проекция точки А; АХ, Аy, АZ – осевые проекции точки А.
Проекции А1, А2, А3 называются соответственно фронтальной, горизонтальной и профильной проекцией точки А.
|
|
Рис. 2.27 |
Рис. 2.28 |
Плоскости проекций, попарно пересекаясь, определяют три оси x, y, z, которые можно рассматривать как систему декартовых координат: ось Х называется осью абцисс, ось y – осью ординат, ось Z – осью аппликат, точка пересечения осей, обозначаемая буквой О, есть начало координат.
7. Плоскость, её задание на чертеже.Положение плоскости в пространстве может быть задано1:Тремя точками, не лежащими на одной прямой. Прямой и точкой вне прямой.Двумя прямыми, пересекающимися в несобственной точке (пересекающимися или параллельными).Соответственно и на чертеже (эпюре) плоскость может быть задана аналогично.Задание плоскости на чертеже производится проекциями этих же геометрических элементов. Кроме того, плоскость может быть задана также проекциями отсека плоской фигуры (Ф).Иногда целесообразно задать плоскость не произвольными пересекающимися прямыми, а прямыми, по которым эта плоскость пересекает плоскости проекций. Эти прямые называют следами плоскости, а такой вариант задания плоскости называют методом задания плоскости следами.Примеры задания плоскости:
Рис.9 |
Тремя точками |
Рис.10 |
Точкой и прямой |
Рис.11 |
Пересекающимися прямыми |
Рис.12 |
Параллельными прямыми |
Рис.13 |
Отсеком плоскости |
11. Пересечение прямой с плоскости
Частные случаи пересечения прямой с плоскостью
Пересечение проецирующей прямой с плоскостью (рис. 4.2,а) определяется из условия принадлежности точки пересечения заданной плоскости (см. тему 3). Пересечение прямой с проецирующей плоскостью (рис. 4.2,а) определяется в пересечении вырожденной проекции плоскости и соответствующей проекции прямой.
На рис. 4.2,б задана фронтально проецирующая плоскость, пересечение вырожденной проекция которой с проекций прямой l'' на эту же плоскость определяет точку пересечения. Как видим, решение позиционных задач при таком расположении простые.
|
|
Рис. 4.2. а) пересечение проецирующей прямой с плоскостью, б) пересечение прямой с проецирующей плоскостью, в)
Линия пересечения двух плоскостей – прямая линия. Рассмотрим сначала частный случай (рис. 3.9), когда одна из
20.Расстояние между двумя параллельными прямыми – определение.
Определение расстояния между двумя параллельными прямыми дается через расстояние от точки до прямой.
Определение.
Расстояние между двумя параллельными прямыми – это расстояние от произвольной точки одной из параллельных прямых до другой прямой.
Для наглядности изобразим две параллельные прямые a и b, отметим на прямой апроизвольную точку М1, опустим перпендикуляр из точки М1 на прямую b, обозначив его H1. Отрезок М1H1 соответствует расстоянию между параллельными прямыми a и b.

Приведенное определение расстояния между двумя параллельными прямыми справедливо как для параллельных прямых на плоскости, так и для прямых в трехмерном пространстве. Более того, такое определение расстояния между двумя параллельными прямыми принято не случайно. Оно тесно связано со следующей теоремой.
Теорема.
Все точки одной из двух параллельных прямых удалены на одинаковое расстояние от другой прямой.
Доказательство.
Рассмотрим
параллельные прямые a и b.
Отметим на прямой a точку М1,
опустим из нее перпендикуляр на прямую b.
Основание этого перпендикуляра обозначим
как H1.
Тогда длина перпендикуляра М1H1 есть
расстояние между параллельными
прямыми a и b по
определению. Докажем, что ![]() равно
равно ![]() ,
где М2 –
произвольная точка прямой a,
отличная от точки M1,
а H2 –
основание перпендикуляра, проведенного
из точки М2 на
прямую b.
Доказав этот факт, мы докажем и саму
теорему.
,
где М2 –
произвольная точка прямой a,
отличная от точки M1,
а H2 –
основание перпендикуляра, проведенного
из точки М2 на
прямую b.
Доказав этот факт, мы докажем и саму
теорему.
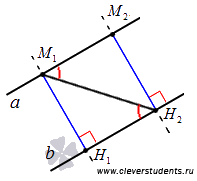
Так
как внутренние накрест лежащие углы,
образованные при пересечении двух
параллельных прямых секущей, равны (об
этом говорилось в статье параллельные
прямые, параллельность прямых),
то ![]() ,
а прямая M2H2,
перпендикулярная прямой b по
построению, перпендикулярна и прямой a.
Тогда треугольники М1H1H2 и М2М1H2 прямоугольные,
и, более того, они равны по гипотенузе
и острому углу: М1H2 –
общая гипотенуза,
.
Из равенства треугольников следует
равенство их соответствующих сторон,
поэтому,
,
а прямая M2H2,
перпендикулярная прямой b по
построению, перпендикулярна и прямой a.
Тогда треугольники М1H1H2 и М2М1H2 прямоугольные,
и, более того, они равны по гипотенузе
и острому углу: М1H2 –
общая гипотенуза,
.
Из равенства треугольников следует
равенство их соответствующих сторон,
поэтому, ![]() .
Теорема доказана.
.
Теорема доказана.
Следует заметить, что расстояние между двумя параллельными прямыми является наименьшим из расстояний от точек одной прямой до точек другой прямой.
ОПРЕДЕЛЕНИЕ ДЛИНЫ ОТРЕЗКА ПРЯМОЙ ЛИНИИ И УГЛОВ НАКЛОНА ПРЯМОЙ К ПЛОСКОСТЯМ ПРОЕКЦИЙ (МЕТОД ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА) |
|
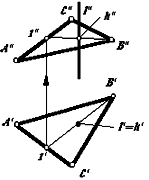
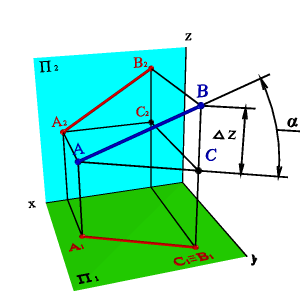
Длину отрезка АВ и - угол наклона отрезка к плоскости П1 можно определить из прямоугольного треугольника АВС |AС|=|A1B1|, |BС|=Z. Для этого на эпюре (рис.31) из точки B1 под углом 900 проводим отрезок |B1B1*|=Z, полученный в результате построений отрезок A1B1* и будет натуральной величиной отрезка АВ, а угол B1A1B1*=. Рассмотренный метод называется методом прямоугольного треугольника. Тот же результат можно получить при вращении треугольника АВС вокруг стороны AС до тех пор, пока он не станет параллелен плоскости П1, в этом случае треугольник проецируется на плоскость проекций без искажения. Подробнее вращение вокруг оси параллельной плоскости проекций рассмотрены в разделе «Методы преобразования ортогональных проекций».
|
|
|
|
|
|||
|
|||
а) модель |
б) эпюр |
||
Рисунок 31. Определение натуральной величины отрезка и угла его наклона к горизонтальной плоскости проекций |
|||
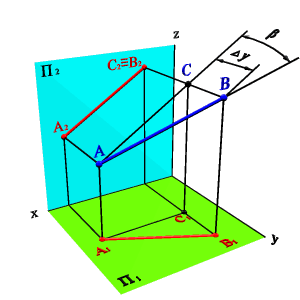
Длину отрезка АВ и -угол наклона отрезка к плоскости П2 можно определить из прямоугольного треугольника АВС |AС|=|A2B2|, |BС|=Y. Построения аналогичные рассмотренным, только в треугольнике АВВ* сторона |BВ*|= и треугольник совмещается с плоскостью П2 (рис.32).
|
|
|
|
|
|||
|
|||
а) модель |
б) эпюр |
||
Рисунок 32. Определение натуральной величины отрезка и угла его наклона к фронтальной плоскости проекций |
|||
26.Пересечение многогранника плоскостью При пересечении многогранника плоскостью получается плоский многоугольник. Вершинами этого многоугольника являются точки пересечения ребер с секущей плоскостью, а сторонами - линии пересечения граней с секущей плоскостью. В связи с этим возможны два метода решения поставленной задачи:
определение точек пересечения ребер с секущей плоскостью;
2)
определение линий пересечения граней
с секущей плоскостью.
 Рис.
56 - Пересечение многогранника
плоскостью
Задача.
Построить линию пересечения пирамиды
SABC с фронтально-проецирующей плоскостью
.
Р
Рис.
56 - Пересечение многогранника
плоскостью
Задача.
Построить линию пересечения пирамиды
SABC с фронтально-проецирующей плоскостью
.
Р
 ис.
57 - Построение линии пересечения пирамиды
с фронтально-проецирующей плоскостью
ис.
57 - Построение линии пересечения пирамиды
с фронтально-проецирующей плоскостью
Рассмотрим построение сечения LMN призмы АВСА'В'С' плоскостью общего положения (DEF). Грани и ребра призмы перпендикулярны П1, а поэтому проецируются на П1 в стороны и вершины треугольника А1В1С1. Для построения фронтальной проекции сечения найдем линии пересечения граней пирамиды с плоскостью DEF.
Нажмите на картинку для просмотра... |
Алгоритм построения:
|
Если ребра пирамиды являются прямыми общего положения, то можно преобразовать чертеж так, чтобы ребра призмы стали проецирующими. В этом случае можно найти точки пересечения ребер призмы с плоскостью сечения. Для нахождения точек М, N, L – точек пересечения ребер пирамиды с плоскостью (EDF) заключим ребра во фронтально проецирущие плоскости , , , которые параллельны между собой.
Нажмите на картинку для просмотра... |
Алгоритм построения:
|