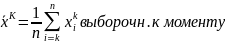35.Эмпирическая функция распределения, гистограмма и их свойства.

Опр.Эмпир. ф-я распред. постр по выборке xV n наз. сл ф-ия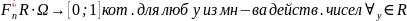

=

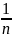
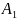
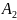
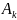
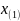
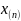
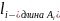
K=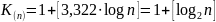

36.Эмпирические моменты и их свойства.

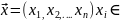Z

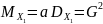
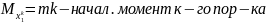
теоритич. хар-ка	эмпиричю. хар-ка
=

Теорема Пусть X  — выборка, 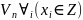c неизвестного функцией распределения  .

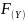— эмпирическая функция распределения, построенная по этой выборке. Тогда для любого y из множества R чисел

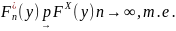
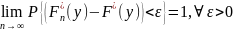
Теорема    Гливенко — Кантелли.

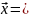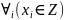) c неизвестного функцией распределения  .

— эмпирическая функция распределения, построенная по этой выборке.

Тогда

Теорема(сходимость эмпирич. моментов)

Имеется выработка 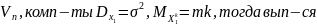след.предел соотн-е

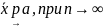
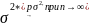
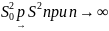
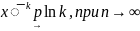
37.Параметрические семейства распределений. Точечные оценки. Несмещенные и состоятельные оценки.

Точечные оценки

Параметрические семейства распределения

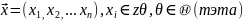
Z

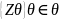
Несмещенные и состоятельные оценки.

Пусть

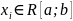
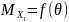
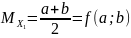
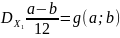
M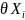

D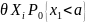

Опр.Стат-ой наз. любая ф-я от компонентов вектора выборки

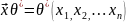
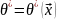
Опр. Стат-ка

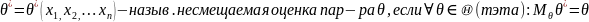
Опр. Посл-ть сл.в.

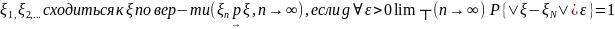
Опр. Ст-ка

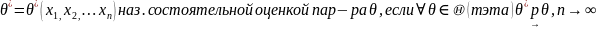
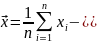случайная веичина

38. Метод моментов

Пусть случайная величина (вектор, матрица и т. д.) X имеет некоторое распределение  , зависящее от параметров  . Пусть для функций (называемых моментами или моментными функциями)  , интегрируемыхпо мере  , выполнены условия на моменты

Пусть   — выборка случайной величины X. Предполагается, что соотношения аналогичные условиям на моменты выполнены и для выборки, а именно вместо математического ожидания в условиях на моменты необходимо использовать выборочные средние:

причем в данном представлении (когда справа от равенства — ноль) достаточно использовать просто суммы вместо средних.

Оценки, получаемые из решения этой системы уравнений (выборочных условий на моменты), называются оценками метода моментов. Название метода связано с тем, что чаще всего в качестве функций   выступают функции степенного вида, математические ожидания от которых в теории вероятностей и математической статистике принято называть моментами.

Если моментные функции непрерывны, то оценки метода моментов состоятельны.

Частные случаи

Некоторые классические методы оценки регрессионных моделей можно представить как частные случаи метода моментов. Например, если линейная регрессионная модель   удовлетворяет условию  , то условия на моменты выглядят следующим образом:

Следовательно, в этом случае оценка метода моментов будет совпадать с оценкой метода наименьших квадратов 

Таким образом, МНК является частным случаем метода моментов, когда выполняется условие ортогональности регрессоров и случайных ошибок 

Рассмотрим другой случай, когда имеются некоторые переменные z, ортогональные случайным ошибкам линейной регрессионной модели, то есть  . Тогда имеем выборочный аналог этого условия:

Следовательно оценка метода моментов будет совпадать с оценкой метода инструментальных переменных:  .

Таким образом, метод инструментальных переменных является частным случаем метода моментов, когда выполнено условие ортогональности инструментов и случайных ошибок модели.
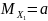
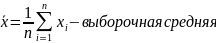