23. 6.2 Равномерное распределение

Плотность вероятности равномерного распределения сохраняет на интервале (a, b) постоянное значение, вне этого интервала плотность вероятности равна нулю. Исходя из основного свойства плотности вероятности, f(x) = 1/(b-a) на интервале (a;b). Интегральную функцию распределения (вероятность того, что с.в. примет значение меньшее, чем x) находим как интеграл от -∞ до x от плотности вероятности: F(x) = (x-a)/(b-a) Графики плотности вероятности и функции равномерного распределения:

Математическое ожидание равномерного распределения: M(X) = (a + b)/2 Дисперсия равномерного распределения: D(X) = (b - a)²/12 Среднее квадратичное отклонение равномерного распределения: σ(X) = (b - a)/(2√3)

24. Показательное (экспоненциальное распределение)

Показательным называют распределение непрерывной случайной величины Х которое

описывается следующей дифференциальной функцией

Экспоненциальное распределение для непрерывных случайных величин является

аналогом распределения Пуассона для дискретных случайных величин и имеет

следующий вид.

вероятность попадания случайной величины Х на интервал (α;β)

Следует отметить, что время безотказной работы удовлетворяется именно

показательному закону, а поэтому это понятие часто используется в понятии

надежности.

25. Нормальный закон распределения (закон Гаусса)

Нормальным называется распределение случайной величины Х если ф-ция плотности

распределения

Полученное выражение через элементарные функции не может быть выражено, такая

функция так называемый интеграл вероятности для которой составлены таблицы,

чаще всего в качестве такой функции используют

Часто по условию задачи необходимо определить вероятность попадания случайной

величины Х на участок симметричный математическому ожиданию.

Правило трех сигм это правило часто используется для подтверждения или

отбрасывания гипотезы о нормальном распределении случайной величины.

25. Нормальный закон распределения (закон Гауса)

Главная особенность в том, что он является предельным законом, к которому приближаются другие распределения, при весьма часто встречающихся типичных условиях.

Нормальный закон распределения характеризуется плотностью вероятности вида:

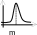
Можно показать, что дисперсия

27. Многомерной случайной величиной называется величина, которая при проведении опыта принимает в качестве своего значения не число, а целый набор чисел, заранее не известно каких. Эти наборы, которые случайная величина может принять, образуют множество ее возможных значений. Таким образом, хотя конкретный набор не предугадаешь, он будет из множества возможных наборов (часто это множество хорошо известно).

Двумерной случайной величиной называют систему из двух случайных величин  , для которой определена вероятность   совместного выполнения неравенств   и  , где x и y - любые действительные числа.     Функция двух переменных

(34)

   определенная для любых x и y, называется функцией распределения системы двух случайных величин   

Ф-цией распред. F_ξη(x, y) двумерной сл.вел-ны (ξ, η) нзв вер-ть совместного выполнения события (ξ<x, η<y), т.е. такая ф-ция F(x, y), к-рая определяет для каждой пары чисел х, у вер-ть того, что ξ примет значение, меньшее х, и при этом η примет значение, меньшее у: F_ξη(x, y)=Р(ξ<x, η<y).

Геометрически это можно истолковать так: F_ξη(x, y) есть вер-ть того, что случ.точка (ξ, η) попадет в бесконечный квадрант с вершиной (х, у), расположенные левее и ниже этой вершины.

Св-ва ф-ции распределения двумерной сл.вел-ны:

1. 0£ F_ξη(x, y)£1 Вытекает из опред-я ф-ции рапред.как вер-ти: вер-ть — всегда неотриц.число, не превышающее 1.

2. F_ξη(x, +∞)= F_ξ(x), т.к. F_ξη(x, +∞)=Р(ξ<x, η<+∞)=Р(ξ<x)= F_ξ(x)

F_ξη(+∞, y)= F_η(y) аналогично

3. F_ξη(x, -∞)= F_ξη(-∞, у)= F_ξη(-∞, -∞)=0. Вытекает из невозможности событий.

F_ξη(+∞, +∞)=1. Вытекает из достоверности событий.

4. F_ξη(x, y) есть монотонно неубывающая ф-ция по каждому аргументу.

Д-во: Событие, состоящее в том, что составляющая ξ примет значение, меньшее х₂, и при этом составляющая η<y, можно подразделить на два несовмест.события: 1) ξ примет значение, меньшее х₁, и при этом η<y с вер-тью Р(ξ<x₁, η<у); 2) ξ примет значение, удовлетворяющее нер-ву х₁£ξ<х₂, и при этом η<y с вер-тью Р(х₁£ξ<х₂, η<y). По теореме сложения, Р(ξ<x₂, η<у)= Р(ξ<x₁, η<у)+ Р(х₁£ξ<х₂, η<y). Отсюда Р(ξ<x₂, η<у) — Р(ξ<x₁, η<у) = Р(х₁£ξ<х₂, η<y) или F_ξη(x₂, y) - F_ξη(x₁, y)= Р(х₁£ξ<х₂, η<y). Любая вер-ть есть число неотриц., поэтому F_ξη(x₂, y) - F_ξη(x₁, y)³0, или F_ξη(x₂, y)³F_ξη(x₁, y) ч.т.д. Аналогично доказывается, что F_ξη(x, y) неубывающая по аргументу у.

5. Если двумерн.ф-ция распред. F_ξη(x, y) непрерывна по х и по у, то вер-ть попадания случ.вел-ны (ξ, η) в прямоугольную область D={х₁ £ x £ х₂, y₁ £ y £y₂} равна Р(х₁£ξ£х₂, у₁£ η £у₂) = F(x₁, y₁)+F(x₂, y₂) — F(x₁, y₂) — F(x₂, y₁).

28. Двумерная случайная величина   называется дискретной, если   и   - дискретные величины.     Пусть возможные значения   и   образуют, например, конечные последовательности x₁, x₂, ..., x_n и y₁, y₂, ..., y_s. Возможные значения двумерной случайной величины   имеют вид (x_i, y_j), где i=1, 2, ..., n; j=1, 2, ..., s. Обозначим через p_ij вероятность того, что     

   Функция распределения F(х, у) имеет вид   

   где двойная сумма распространена на те i и j, для которых x_i<x и y_j<y. 

Законом распред.дискретной двумерной сл.вел-ны нзв перечень возможных значений этой вел-ны, т.е пар чисел (x_i, y_j) и их вероятностей р(x_i, y_j) (i=1, 2,…,n; j=1, 2,…, m). Обычно закон распределения задают в виде матрицы. Матрица распред.предст.соб.таблицу, к-рая содержит значения {x₁, x₂,…, x_n}, {y₁, y₂,…, y_n} и вероятности возможных пар значений P_ij=P(ξ=x_i; η=y_j) (i=1, 2,…,n; j=1, 2,…, m).

	y1	y2	…	ym
x1	P11	P12	…	P1m
x2	P21	P22	…	P2m
…	…	…	…	…
xn	Pn1	Pn2	…	Pnm

29. Непрерывная двумерная с.в. Плотность распределения.

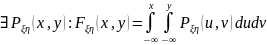
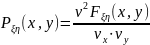
Св-ва :

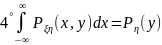
30. Ковариация. Коэффициент корреляции. Свойства коэффициента корреляции

Свойства

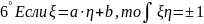
31. Неравенства Чебышева.

Теорема: Для любой 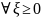,имеющий справедливы следующие неравенства (1)

(2)

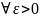
Док-во:

η

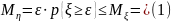
η= =>(1)

=>

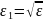=> (2)

Закон больших чисел в форме Чебышева

Теорема: если сл.велч. попарно независимы

Док-во:

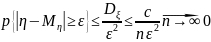
32. Закон больших чисел в форме Бернулли

Теорема: Пусть M- число У в n ИБ с P(y)=p , тогда: относит частота успеха

,

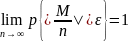- относит. частота

ДОК-ВО: Введем индикатор того, что

=

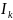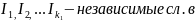
ЗБЧ(в форме чеб.) =>

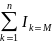
33. Понятие о центральной предельной теореме

Определение: Говорят что послед-ть сл.вл.: удовл.ЦПТ, если справедливо соотношение для частичных сумм этих сл.в: = = 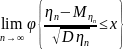∙ 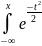dt = -стан-

х

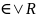
ЦПТ для независимых одинаково распределенных сл.в

Если - независимы , имеют одинаковое распределение, т.е. = , K =1,2...,то

34.Генеральная совокупность, выборка, выборочный метод. Вариационный ряд. Порядковые статистики.

Генеральной совокупностью называют совокупность объектов, из которых производится выборка.

Объемом совокупности (выборочной или генеральной) называют число объектов этой совокупности. Например, если из 1000 деталей отобрано для обследования 100 деталей, то объем генеральной совокупности N = 1000, а объем выборки я =100.

Замечание. Часто генеральная совокупность содержит конечное число объектов. Однако если это число достаточно велико, то иногда в целях упрощения вычислений, или для облегчения теоретических выводов, допускают, что генеральная совокупность состоит из бесчисленного множества объектов. Такое допущение оправдывается тем, что увеличение объема генеральной совокупности (достаточно большого объема) практически не сказывается на результатах

обработки данных выборки.

Вариационный ряд

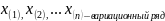
Порядковые статистики.

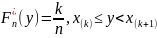
1,y