
- •2.Случайные события. И операции над ними.
- •3.Вероятность в случае дискретного пэи. Классическое определение вероятности.
- •4. Свойства вероятности
- •5. Некоторые понятия комбинаторики
- •6. Геометрические вероятности.
- •7. Аксиоматическое определение вероятности случайных событий.
- •8. Условная вероятность. Независимость событий. Формулы сложения и умножения.
- •9. Формула полной вероятности. Формула Байеса.
- •10.Схема Бернулли. Теорема Бернулли.
- •11. Предельные теоремы в схеме Бернулли. Теорема Пуассона. Локальная теорема Муавра - Лапласа.
- •13. Определение случайной величины. Дискретная с.В. Ряд распределения.
- •14. Функция распределения. Св и её свойства.
- •15. Непрерывная с.В. Плотность распределения и ее свойства.
- •16.Математическое ожидание дискретной и непрерывной с.В. (мо). Мода. Медиана.
- •17.Начальные и центральные моменты порядка к.
- •18.Дисперсия и ее свойства. Асимметрия и эксцесс.
- •19. Биноминальный закон распределение.
- •20.Распределение Пуассона.
- •22. Гипергеометрическое распределение
- •23. 6.2 Равномерное распределение
- •24. Показательное (экспоненциальное распределение)
- •25. Нормальный закон распределения (закон Гаусса)
- •25. Нормальный закон распределения (закон Гауса)
- •35.Эмпирическая функция распределения, гистограмма и их свойства.
- •36.Эмпирические моменты и их свойства.
- •37.Параметрические семейства распределений. Точечные оценки. Несмещенные и состоятельные оценки.
- •38. Метод моментов
- •39. Метод максимального правдоподобия.
- •Условный метод максимального правдоподобия
- •41. Неравенство Крамера — Рао
- •42. Интервальные оценки. Доверительный интервал. Общие принципы построения доверительных интервалов.
- •43. Статистическая проверка гипотез. Критерии. Ошибки I-ого рода.
- •44. Способы сравнения критериев. Наиболее мощные критерии. Лемма Неймана-Пирсона.
- •Способы сравнения критериев
41. Неравенство Крамера — Рао
В математической статистике неравенством Краме́ра — Ра́о (в честь Гаральда Крамера и К. Р. Рао) называется неравенство, которое при некоторых условиях на статистическую модель даёт нижнюю границу для дисперсии оценки неизвестного параметра, выражая её через информацию Фишера.
Формулировка
Пусть
дана статистическая
модель ![]() ,
, ![]() — выборка размера
— выборка размера ![]() ,
определена функция
правдоподобия
,
определена функция
правдоподобия 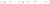 и
выполнены следующие условия (условия
регулярности):
и
выполнены следующие условия (условия
регулярности):
![]() и
везде дифференцируема по
.
и
везде дифференцируема по
.
Функция  (функция
вклада выборки) имеет конечную дисперсию (или,
что то же, конечнаинформация
Фишера).
(функция
вклада выборки) имеет конечную дисперсию (или,
что то же, конечнаинформация
Фишера).
Для
любой статистики ![]() с
конечным вторым моментом имеет место
равенство
с
конечным вторым моментом имеет место
равенство
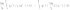 .
.
Пусть
при этих условиях дана статистика
,
которая несмещённо оценивает
дифференцируемую функцию ![]() .
Тогда справедливо следующее неравенство:
.
Тогда справедливо следующее неравенство:
![]() ;
;
равенство
достигается тогда и только тогда,
когда ![]() представляется
в виде
представляется
в виде ![]() .
.
Здесь ![]() — информация
Фишера.
— информация
Фишера.
42. Интервальные оценки. Доверительный интервал. Общие принципы построения доверительных интервалов.
Доверительный интервал — термин, используемый в математической статистике при интервальной (в отличие от точечной) оценке статистических параметров, что предпочтительнее при небольшом объёме выборки. Доверительным называют интервал, который покрывает неизвестный параметр с заданной надёжностью.
Метод доверительных интервалов разработал американский статистик Ежи Нейман, исходя из идей английского статистикаРональда Фишера
Определение
Доверительным
интервалом параметра θ распределения случайной
величины X с уровнем доверия
100p%[примечание
1], порождённым выборкой (x1,…,xn),
называется интервал с границами ![]() (x1,…,xn)
и
(x1,…,xn)
и ![]() (x1,…,xn),
которые являются реализациями случайных
величин L(X1,…,Xn) и U(X1,…,Xn), таких,
что
(x1,…,xn),
которые являются реализациями случайных
величин L(X1,…,Xn) и U(X1,…,Xn), таких,
что
![]() .
.
Граничные точки доверительного интервала и называются доверительными пределами.
Интерпретация доверительного интервала, основанная на интуиции, будет следующей: если p велико (скажем, 0,95 или 0,99), то доверительный интервал почти наверняка содержит истинное значение θ.[ссылка 2]
Еще одно истолкование понятию доверительного интервала: его можно рассматривать как интервал значений параметра θ, совместимых с опытными данными и не противоречащих им.
43. Статистическая проверка гипотез. Критерии. Ошибки I-ого рода.
Статистическая гипотеза (statistical hypothesys) — это определённое предположение о распределении вероятностей, лежащем в основе наблюдаемой выборки данных.
Методика проверки статистических гипотез
Пусть
задана случайная выборка ![]() —
последовательность
—
последовательность ![]() объектов
из множества
объектов
из множества ![]() .
Предполагается, что на множестве
существует
некоторая неизвестная вероятностная
мера
.
Предполагается, что на множестве
существует
некоторая неизвестная вероятностная
мера ![]() .
.
Методика состоит в следующем.
Формулируется нулевая гипотеза
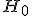 о распределении
вероятностей на множестве
.
Гипотеза формулируется исходя из
требований прикладной задачи. Чаще
всего рассматриваются две гипотезы
— основная или нулевая
и
альтернативная
о распределении
вероятностей на множестве
.
Гипотеза формулируется исходя из
требований прикладной задачи. Чаще
всего рассматриваются две гипотезы
— основная или нулевая
и
альтернативная 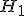 .
Иногда альтернатива не формулируется
в явном виде; тогда предполагается,
что
означает
«не
».
Иногда рассматривается сразу несколько
альтернатив. В математической
статистике хорошо изучено несколько
десятков «наиболее часто встречающихся»
типов гипотез, и известны ещё сотни
специальных вариантов и разновидностей.
Примеры приводятся ниже.
.
Иногда альтернатива не формулируется
в явном виде; тогда предполагается,
что
означает
«не
».
Иногда рассматривается сразу несколько
альтернатив. В математической
статистике хорошо изучено несколько
десятков «наиболее часто встречающихся»
типов гипотез, и известны ещё сотни
специальных вариантов и разновидностей.
Примеры приводятся ниже.Задаётся некоторая статистика (функция выборки)
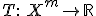 ,
для которой в условиях справедливости
гипотезы
выводится функция
распределения
,
для которой в условиях справедливости
гипотезы
выводится функция
распределения 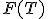 и/или плотность
распределения
и/или плотность
распределения 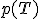 .
Вопрос о том, какую статистику надо
взять для проверки той или иной гипотезы,
часто не имеет однозначного ответа.
Есть целый ряд требований, которым
должна удовлетворять «хорошая»
статистика
.
Вопрос о том, какую статистику надо
взять для проверки той или иной гипотезы,
часто не имеет однозначного ответа.
Есть целый ряд требований, которым
должна удовлетворять «хорошая»
статистика 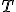 .
Вывод функции распределения
при
заданных
и
является
строгой математической задачей, которая
решается методами теории вероятностей;
в справочниках приводятся готовые
формулы для
;
в статистических пакетах имеются
готовые вычислительные процедуры.
.
Вывод функции распределения
при
заданных
и
является
строгой математической задачей, которая
решается методами теории вероятностей;
в справочниках приводятся готовые
формулы для
;
в статистических пакетах имеются
готовые вычислительные процедуры.Фиксируется уровень значимости — допустимая для данной задачи вероятность ошибки первого рода, то есть того, что гипотеза на самом деле верна, но будет отвергнута процедурой проверки. Это должно быть достаточно малое число
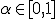 .
На практике часто полагают
.
На практике часто полагают 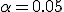 .
.На множестве допустимых значений статистики выделяется критическое множество
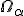 наименее
вероятных значений статистики
,
такое, что
наименее
вероятных значений статистики
,
такое, что 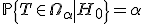 .
Вычисление границ критического множества
как функции от уровня значимости
.
Вычисление границ критического множества
как функции от уровня значимости  является
строгой математической задачей, которая
в большинстве практических случаев
имеет готовое простое решение.
является
строгой математической задачей, которая
в большинстве практических случаев
имеет готовое простое решение.Собственно статистический тест (статистический критерий) заключается в проверке условия:
если
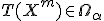 ,
то делается вывод «данные противоречат
нулевой гипотезе при уровне значимости
,
то делается вывод «данные противоречат
нулевой гипотезе при уровне значимости 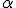 ».
Гипотеза отвергается.
».
Гипотеза отвергается.если
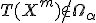 ,
то делается вывод «данные не противоречат
нулевой гипотезе при уровне значимости
».
Гипотеза принимается.
,
то делается вывод «данные не противоречат
нулевой гипотезе при уровне значимости
».
Гипотеза принимается.
Итак, статистический критерий определяется статистикой и критическим множеством , которое зависит от уровня значимости .
Замечание. Если данные не противоречат нулевой гипотезе, это ещё не значит, что гипотеза верна. Тому есть две причины.
По мере увеличения длины выборки нулевая гипотеза может сначала приниматься, но потом выявятся более тонкие несоответствия данных гипотезе, и она будет отвергнута. То есть многое зависит от объёма данных; если данных не хватает, можно принять даже самую неправдоподобную гипотезу.
Выбранная статистика может отражать не всю информацию, содержащуюся в гипотезе . В таком случае увеличивается вероятность ошибки второго рода — нулевая гипотеза может быть принята, хотя на самом деле она не верна. Допустим, например, что = «распределение нормально»;
 =
«коэффициент
асимметрии»; тогда выборка с любым
симметричным распределением будет
признана нормальной. Чтобы избегать
таких ошибок, следует пользоваться
более мощными
критериями.
=
«коэффициент
асимметрии»; тогда выборка с любым
симметричным распределением будет
признана нормальной. Чтобы избегать
таких ошибок, следует пользоваться
более мощными
критериями.
